Statistical Relationships

Correlation Analysis

Correlation Analysis คือ วิธีการทางสถิติที่ใช้ศึกษาความสัมพันธ์ระหว่างตัวแปรสองตัวหรือมากกว่า ว่ามีความสัมพันธ์กันหรือไม่ และมีความสัมพันธ์กันในทิศทางใด โดยจะพิจารณาว่าเมื่อตัวแปรหนึ่งเปลี่ยนแปลงไป ตัวแปรอีกตัวจะเปลี่ยนแปลงไปในทิศทางใดและในระดับใด

โดย Correlation Analysis มี Correlation Coefficient เป็นตัวบ่งชี้ความสัมพันธ์ ซึ่งมีค่าอยู่ระหว่าง -1 ถึง +1 อยู่

• ค่า +1 แสดงถึงความสัมพันธ์เชิงบวกที่สมบูรณ์แบบ หมายความว่าเมื่อตัวแปรหนึ่งเพิ่มขึ้น อีกตัวแปรหนึ่งก็จะเพิ่มขึ้นในอัตราส่วนที่คงที่
• ค่า -1 แสดงถึงความสัมพันธ์เชิงลบที่สมบูรณ์แบบ หมายความว่าเมื่อตัวแปรหนึ่งเพิ่มขึ้น อีกตัวแปรหนึ่งจะลดลงในอัตราส่วนที่คงที่
• ค่า 0 แสดงว่าไม่มีความสัมพันธ์เชิงเส้นระหว่างตัวแปรทั้งสอง

ตัวอย่างเช่น

• ความสัมพันธ์ระหว่างความสูงและน้ำหนักของคน โดยทั่วไปแล้วคนที่มีความสูงมากขึ้นก็มักจะมีน้ำหนักมากขึ้น ซึ่งแสดงถึงความสัมพันธ์เชิงบวก
• ความสัมพันธ์ระหว่างราคาสินค้าและความต้องการซื้อ เมื่อราคาสินค้าสูงขึ้น ความต้องการซื้อก็จะลดลง ซึ่งแสดงถึงความสัมพันธ์เชิงลบ

โดยปกติ วิธีการคำนวน Correlation Analysis จะมี 2 Idea ใหญ่ๆที่มักจะชอบใช้กัน

1. Pearson Correlation ใช้สำหรับตัวแปรที่มีการวัดในระดับช่วง (Interval) หรืออัตราส่วน (Ratio) และมีการแจกแจงแบบปกติ (Normal Distribution)
2. Spearman Correlation ใช้สำหรับตัวแปรที่มีการวัดในระดับเรียงอันดับ (Ordinal) หรือเมื่อข้อมูลไม่มีการแจกแจงแบบปกติ

โดยใน python นั้น สามารถคำนวณทั้ง Pearson Correlation และ Spearman Correlation ได้อย่างง่าย โดยใช้ library scipy.stats ซึ่งเป็นส่วนหนึ่งของ SciPy ecosystem ที่มีความนิยมในการคำนวณทางวิทยาศาสตร์และสถิติใน Python

แต่ก่อนที่เราจะดูส่วน code เพื่อให้เกิดความเข้าใจ เราจะอธิบาย Correlation ทั้ง 2 แบบกันก่อน

Pearson Correlation

Pearson Correlation คือ ค่าที่ใช้วัดความสัมพันธ์เชิงเส้นระหว่างตัวแปรสองตัว โดยค่าที่ได้จะแสดงระดับและทิศทางของความสัมพันธ์ โดยค่ามีช่วงระหว่าง 1 ถึง 1 ให้ความหมายว่า

• 1 หมายถึง ความสัมพันธ์เชิงเส้นที่สมบูรณ์แบบในทิศทางเดียวกัน (positive correlation)
• 1 หมายถึง ความสัมพันธ์เชิงเส้นที่สมบูรณ์แบบในทิศทางตรงกันข้าม (negative correlation)
• 0 หมายถึง ไม่มีความสัมพันธ์เชิงเส้น

สูตรการคำนวณ

$$r = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum (x_i - \bar{x})^2 \sum (y_i - \bar{y})^2}}$$

โดย:

• r = Pearson Correlation Coefficient
• $x_i$ , $y_i$ = ค่าใน dataset ของตัวแปร x และ y
• $\bar{x}$, $\bar{y}$ = ค่าเฉลี่ยของตัวแปร x และ y

ขั้นตอนการคำนวณ

1. คำนวณค่าเฉลี่ยของตัวแปร x (x̄) และตัวแปร y (ȳ)
2. สำหรับแต่ละข้อมูล คำนวณ (xi - x̄) และ (yi - ȳ)
3. คำนวณผลคูณของ (xi - x̄) และ (yi - ȳ) สำหรับแต่ละข้อมูล จากนั้นนำผลคูณทั้งหมดมารวมกัน (Σ[(xi - x̄)(yi - ȳ)])
4. คำนวณ (xi - x̄)² สำหรับแต่ละข้อมูล จากนั้นนำผลรวมทั้งหมด (Σ(xi - x̄)²)
5. คำนวณ (yi - ȳ)² สำหรับแต่ละข้อมูล จากนั้นนำผลรวมทั้งหมด (Σ(yi - ȳ)²)
6. นำผลรวมในขั้นตอนที่ 3 หารด้วยรากที่สองของผลคูณระหว่างผลรวมในขั้นตอนที่ 4 และ 5

ตัวอย่างการคำนวณ

สมมติว่าเราต้องการหาความสัมพันธ์ระหว่างชั่วโมงการเรียน (x) และคะแนนสอบ (y) มีข้อมูลดังนี้

ชั่วโมงการเรียน (x)	คะแนนสอบ (y)
2	50
4	60
6	70
8	80

1. คำนวณค่าเฉลี่ย:
   • x̄ = (2 + 4 + 6 + 8) / 4 = 5
   • ȳ = (50 + 60 + 70 + 80) / 4 = 65
2. คำนวณ (xi - x̄) และ (yi - ȳ):

ชั่วโมงการเรียน (x)	คะแนนสอบ (y)	xi - x̄	yi - ȳ
2	50	-3	-15
4	60	-1	-5
6	70	1	5
8	80	3	15

1. คำนวณ Σ[(xi - x̄)(yi - ȳ)]
   • (-3)(-15) + (-1)(-5) + (1)(5) + (3)(15) = 45 + 5 + 5 + 45 = 100
2. คำนวณ Σ(xi - x̄)²
   • (-3)² + (-1)² + (1)² + (3)² = 9 + 1 + 1 + 9 = 20
3. คำนวณ Σ(yi - ȳ)²
   • (-15)² + (-5)² + (5)² + (15)² = 225 + 25 + 25 + 225 = 500
4. คำนวณ r
   • r = 100 / √(20 * 500) = 100 / √10000 = 100 / 100 = 1

ในตัวอย่างนี้ r = 1 ซึ่งแสดงว่ามีสหสัมพันธ์เชิงบวกที่สมบูรณ์แบบระหว่างชั่วโมงการเรียนและคะแนนสอบ

หากใช้วิธีนี้ใน python จะสามารถเขียนเป็น code ได้ลักษณะนี้

import numpy as np
import scipy.stats as stats

x = np.array([2, 4, 6, 8])  # ชั่วโมงการเรียน
y = np.array([50, 60, 70, 80])  # คะแนนสอบ

# คำนวณ Pearson correlation
correlation_coefficient, p_value = stats.pearsonr(x, y)

print(f"Pearson Correlation Coefficient (r): {correlation_coefficient}")
print(f"P-value: {p_value}")

# แสดงผลแบบละเอียด (ทำตามขั้นตอนที่อธิบายไว้ก่อนหน้า)
x_mean = np.mean(x)
y_mean = np.mean(y)

numerator = np.sum((x - x_mean) * (y - y_mean))
denominator = np.sqrt(np.sum((x - x_mean)**2) * np.sum((y - y_mean)**2))

correlation_manual = numerator / denominator

print("\nCalculation Breakdown (Manual):")
print(f"Mean of x (x̄): {x_mean}")
print(f"Mean of y (ȳ): {y_mean}")
print(f"Numerator (Σ[(xi - x̄)(yi - ȳ)]): {numerator}")
print(f"Denominator (√[Σ(xi - x̄)² * Σ(yi - ȳ)²]): {denominator}")
print(f"Pearson Correlation Coefficient (r): {correlation_manual}")

# แสดงผลโดยใช้ pandas (เพื่อเปรียบเทียบ)
import pandas as pd

data = {'Hours': x, 'Scores': y}
df = pd.DataFrame(data)
correlation_pandas = df['Hours'].corr(df['Scores'])
print(f"\nPearson Correlation Coefficient (r) using Pandas: {correlation_pandas}")

ผลลัพธ์

Pearson Correlation Coefficient (r): 1.0
P-value: 0.0
Calculation Breakdown (Manual):
Mean of x (x̄): 5.0
Mean of y (ȳ): 65.0
Numerator (Σ[(xi - x̄)(yi - ȳ)]): 100.0
Denominator (√[Σ(xi - x̄)² * Σ(yi - ȳ)²]): 100.0
Pearson Correlation Coefficient (r): 1.0

Pearson Correlation Coefficient (r) using Pandas: 1.0

คำอธิบาย

• ใช้ numpy.array เพื่อเก็บข้อมูล x และ y ในรูปแบบ array ซึ่งทำให้การคำนวณทางคณิตศาสตร์ทำได้ง่ายและรวดเร็ว
• stats.pearsonr(x, y) คืนค่าสองค่า คือ r และค่า p-value ซึ่งใช้ในการทดสอบนัยสำคัญทางสถิติ ในกรณีนี้ p-value เป็น 0 ซึ่งหมายความว่ามีความสัมพันธ์อย่างมีนัยสำคัญทางสถิติ
• เราสามารถหาค่า Correlation ได้ง่ายๆด้วย method .corr() ใน pandas

(สำหรับ p-value เดี๋ยวเรามีอธิบายอีกทีในหัวข้อ Hypothesis Testing)

ข้อควรระวังในการใช้

• Pearson Correlation วัดเฉพาะความสัมพันธ์เชิงเส้น หากความสัมพันธ์เป็นแบบอื่น เช่น โค้ง Pearson Correlation อาจให้ผลลัพธ์ที่ไม่ถูกต้อง
• Correlation ไม่ได้หมายถึง Causation (ความเป็นเหตุเป็นผล) การที่ตัวแปรสองตัวมีความสัมพันธ์กัน ไม่ได้หมายความว่าตัวแปรหนึ่งเป็นสาเหตุของอีกตัวแปรหนึ่ง

Spearman Correlation

Spearman Correlation คือ การวัดความสัมพันธ์แบบ monotonic ระหว่างตัวแปรสองตัว โดยเน้นที่การดูว่าเมื่อตัวแปรหนึ่งมีแนวโน้มเพิ่มขึ้นหรือลดลง อีกตัวแปรหนึ่งมีแนวโน้มที่จะเปลี่ยนแปลงไปในทิศทางเดียวกันหรือไม่ โดยไม่สนใจว่าการเปลี่ยนแปลงนั้นจะเป็นเส้นตรงหรือไม่ ทำให้ Spearman Correlation เหมาะกับข้อมูลที่ไม่ได้มีการแจกแจงแบบปกติ หรือข้อมูลที่อยู่ในระดับเรียงอันดับ (Ordinal Scale) เช่น อันดับความชอบ ระดับความพึงพอใจ หรือคะแนนการประเมิน เป็นต้น

Spearman Correlation จะคำนวณหาค่าสัมประสิทธิ์สหสัมพันธ์สเปียร์แมน (Spearman rank correlation coefficient) ซึ่งมักแทนด้วยตัวอักษร ρ (rho) หรือ rs โดยมีค่าอยู่ระหว่าง -1 ถึง +1 เช่นเดียวกับ Pearson Correlation

• ρ = +1 แสดงว่ามีความสัมพันธ์แบบ monotonic เชิงบวกที่สมบูรณ์แบบ หมายความว่าเมื่อตัวแปรหนึ่งเพิ่มขึ้น อีกตัวแปรหนึ่งก็มีแนวโน้มที่จะเพิ่มขึ้นเสมอ (ไม่จำเป็นต้องเพิ่มขึ้นในอัตราส่วนคงที่)
• ρ = -1 แสดงว่ามีความสัมพันธ์แบบ monotonic เชิงลบที่สมบูรณ์แบบ หมายความว่าเมื่อตัวแปรหนึ่งเพิ่มขึ้น อีกตัวแปรหนึ่งก็มีแนวโน้มที่จะลดลงเสมอ
• ρ = 0 แสดงว่าไม่มีความสัมพันธ์แบบ monotonic ระหว่างตัวแปรทั้งสอง

สูตรที่ใช้คำนวณ Spearman Correlation คือ

$$\rho = 1 - \frac{6 \sum d_i^2}{n(n^2 - 1)}$$

โดยที่

• $d_i$ คือ ผลต่างของอันดับ (rank) ของแต่ละข้อมูลในตัวแปรทั้งสอง
• n คือ จำนวนข้อมูล

ขั้นตอนการคำนวณ

1. เรียงอันดับข้อมูลของตัวแปรแต่ละตัว โดยให้อันดับ 1 กับข้อมูลที่มีค่าน้อยที่สุด (หรือมากที่สุด แล้วแต่กำหนด)
2. คำนวณผลต่างของอันดับ ($d_i$) ของแต่ละคู่ข้อมูล
3. ยกกำลังสองของผลต่างอันดับ ($d_i^²$)
4. คำนวณผลรวมของ $d_i^²$ ($\sum d_i^²$)
5. แทนค่าทั้งหมดในสูตร

ตัวอย่างการคำนวณ

สมมติว่าเราต้องการหาความสัมพันธ์ระหว่างอันดับความชอบหนังสองเรื่อง (X และ Y) มีข้อมูลดังนี้ (สมมติว่ามีคน 5 คนให้คะแนน)

คน	อันดับความชอบหนัง X	อันดับความชอบหนัง Y
A	1	3
B	2	1
C	3	2
D	4	5
E	5	4

1. คำนวณผลต่างของอันดับ ($d_i$)

คน	อันดับ X	อันดับ Y	di
A	1	3	-2
B	2	1	1
C	3	2	1
D	4	5	-1
E	5	4	1

1. คำนวณ $d_i^²$

คน	di	di²
A	-2	4
B	1	1
C	1	1
D	-1	1
E	1	1

1. คำนวณ Σdi²: 4 + 1 + 1 + 1 + 1 = 8
2. แทนค่าในสูตร (n = 5): ρ = 1 - (6 * 8) / [5(5² - 1)] = 1 - 48 / (5 * 24) = 1 - 48 / 120 = 1 - 0.4 = 0.6

ในตัวอย่างนี้ ρ = 0.6 แสดงว่ามีความสัมพันธ์แบบ monotonic เชิงบวกในระดับปานกลางระหว่างอันดับความชอบหนังทั้งสองเรื่อง

ลองมาดูตัวอย่างฉบับ code python กันบ้าง

import scipy.stats as stats
import numpy as np

x = np.array([1, 2, 3, 4, 5]) # อันดับความชอบหนัง X
y = np.array([3, 1, 2, 5, 4]) # อันดับความชอบหนัง Y

correlation, p_value = stats.spearmanr(x, y)

print(f"Spearman Correlation Coefficient (ρ): {correlation}")
print(f"P-value: {p_value}")

# pandas example
import pandas as pd
data = {'Rank_X': x, 'Rank_Y': y}
df = pd.DataFrame(data)
correlation_pandas = df['Rank_X'].corr(df['Rank_Y'], method='spearman')
print(f"Spearman Correlation Coefficient (ρ) using Pandas: {correlation_pandas}")

ผลลัพธ์

Spearman Correlation Coefficient (ρ): 0.6
P-value: 0.2886751345948129
Spearman Correlation Coefficient (ρ) using Pandas: 0.6

ความแตกต่างระหว่าง Pearson และ Spearman:

• Pearson: วัดความสัมพันธ์เชิงเส้น เหมาะกับข้อมูลที่ต่อเนื่องและมีการแจกแจงแบบปกติ
• Spearman: วัดความสัมพันธ์แบบ monotonic เหมาะกับข้อมูลที่ไม่มีการแจกแจงแบบปกติ หรือข้อมูลเชิงอันดับ

การเลือกว่าจะใช้ Pearson หรือ Spearman ขึ้นอยู่กับลักษณะของข้อมูลและความสัมพันธ์ที่ต้องการศึกษา หากต้องการดูความสัมพันธ์แบบเส้นตรง และข้อมูลมีการแจกแจงปกติ ให้ใช้ Pearson แต่ถ้าต้องการดูแนวโน้มความสัมพันธ์ (เพิ่มขึ้นหรือลดลง) โดยไม่สนใจว่าจะเป็นเส้นตรงหรือไม่ หรือข้อมูลอยู่ในรูปของอันดับ ให้ใช้ Spearman

Correlation Matrix

Correlation Matrix คือตารางที่แสดงค่า Correlation Coefficient ระหว่างตัวแปรหลายคู่ในชุดข้อมูลเดียวกัน โดยจะช่วยให้เราเห็นภาพรวมของความสัมพันธ์ระหว่างตัวแปรต่างๆ ได้อย่างรวดเร็ว และระบุได้ว่าตัวแปรใดมีความสัมพันธ์กันมากน้อยเพียงใด และเป็นไปในทิศทางใด

รูปแบบของ Correlation Matrix

• Matrix จะมีลักษณะเป็นตารางจัตุรัส (Square Matrix) โดยมีจำนวนแถวและหลักเท่ากับจำนวนตัวแปร
• ช่องในแนวทแยงมุม (Diagonal) จะมีค่าเป็น 1 เสมอ เพราะแสดงถึงความสัมพันธ์ของตัวแปรกับตัวเอง
• ช่องอื่นๆ จะแสดงค่า Correlation Coefficient ระหว่างตัวแปรในแถวและหลักนั้นๆ ค่าที่แสดงอาจเป็น Pearson Correlation หรือ Spearman Correlation ขึ้นอยู่กับวิธีการคำนวณที่เลือกใช้
• Matrix จะเป็นสมมาตร (Symmetric) หมายความว่าค่าในช่อง (i, j) จะเท่ากับค่าในช่อง (j, i) เนื่องจากความสัมพันธ์ระหว่างตัวแปร A กับ B ก็เหมือนกับความสัมพันธ์ระหว่าง B กับ A

เช่นตัวอย่างใน code python นี้

เราจะยกตัวอย่างการสร้าง Correlation Matrix ด้วย Python โดยใช้ library pandas และ seaborn เพื่อแสดงผลเป็นภาพออกมา

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

# สร้างข้อมูลตัวอย่าง (Random Data)
np.random.seed(0)  # เพื่อให้ได้ผลลัพธ์ที่เหมือนเดิมทุกครั้ง
num_samples = 50
data = {
    'Variable_A': np.random.rand(num_samples) * 10,
    'Variable_B': np.random.rand(num_samples) * 10 + 2,
    'Variable_C': np.random.rand(num_samples) * 10 - 5,
    'Variable_D': np.random.rand(num_samples) * 10 * 0.5 + np.random.rand(num_samples)*5 # สร้างความสัมพันธ์กับ variable A บ้าง
}

df = pd.DataFrame(data)

# คำนวณ Correlation Matrix (Pearson)
correlation_matrix_pearson = df.corr(method='pearson')

# แสดงผลด้วย Heatmap (seaborn)
plt.figure(figsize=(8, 6))
sns.heatmap(correlation_matrix_pearson, annot=True, cmap='coolwarm', fmt=".2f")
plt.title("Pearson Correlation Matrix")
plt.show()

# คำนวณ Correlation Matrix (Spearman)
correlation_matrix_spearman = df.corr(method='spearman')

# แสดงผลด้วย Heatmap (seaborn)
plt.figure(figsize=(8, 6))
sns.heatmap(correlation_matrix_spearman, annot=True, cmap='coolwarm', fmt=".2f")
plt.title("Spearman Correlation Matrix")
plt.show()

#ตัวอย่างการเข้าถึงค่าใน Correlation Matrix
print("\nเข้าถึงค่า correlation ระหว่าง Variable_A กับ Variable_B แบบ pearson : ", correlation_matrix_pearson.loc['Variable_A','Variable_B'])

ผลลัพธ์

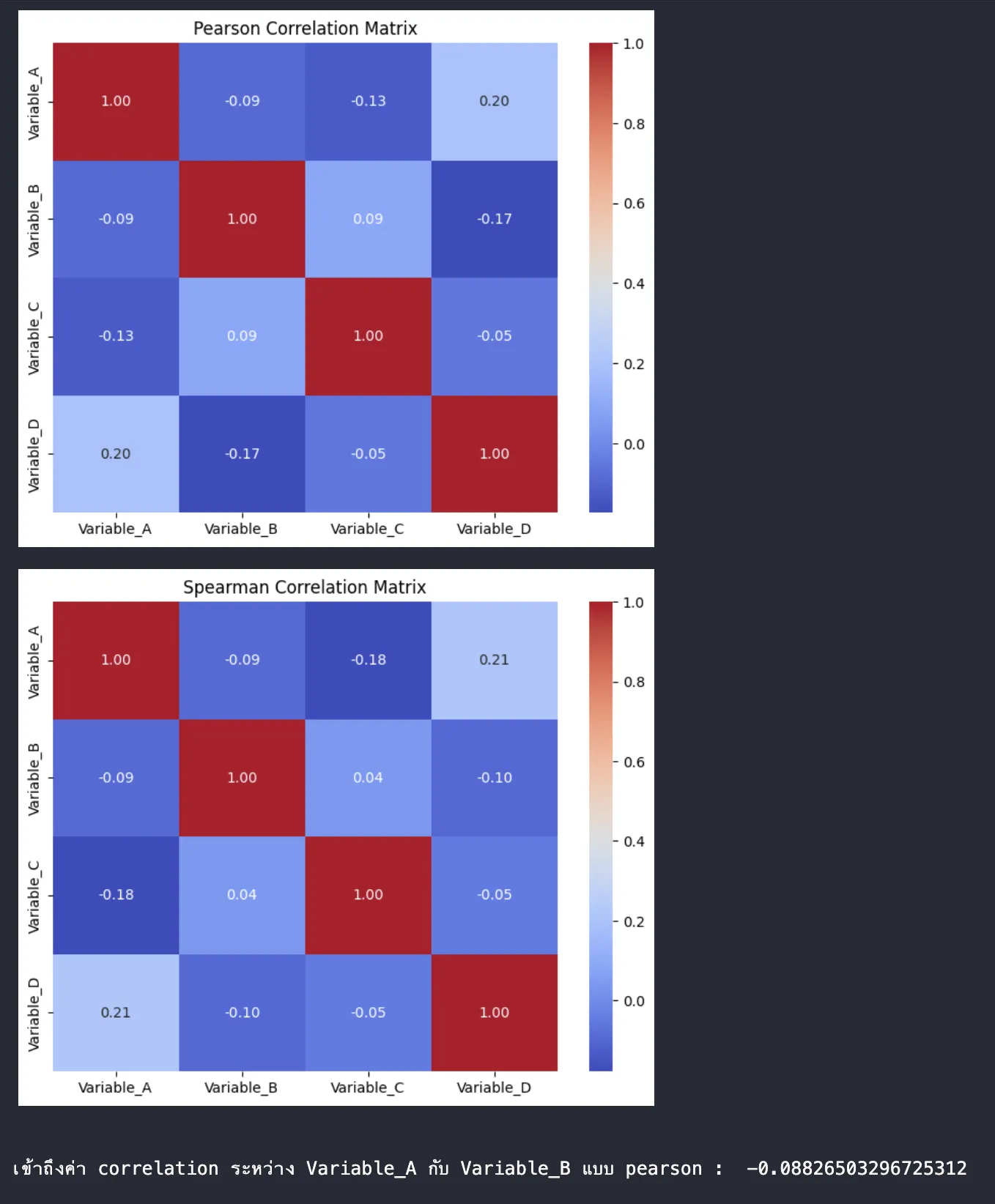
จาก code ชุดนี้

• สร้างข้อมูลตัวอย่างโดยใช้ numpy.random.rand() เพื่อสร้างตัวเลขสุ่ม
• สร้าง pandas.DataFrame จากข้อมูล
• ใช้ df.corr() เพื่อคำนวณ Correlation Matrix โดยกำหนด method='pearson' หรือ method='spearman' เพื่อเลือกวิธีการคำนวณ
• ใช้ seaborn.heatmap() เพื่อแสดงผล Correlation Matrix เป็น Heatmap ซึ่งจะใช้สีแสดงระดับความสัมพันธ์ ทำให้ง่ายต่อการมองเห็น

ผลลัพธ์ที่ได้มาคือ code จะสร้าง Heatmap สองรูป รูปแรกแสดง Pearson Correlation Matrix และรูปที่สองแสดง Spearman Correlation Matrix พร้อมค่าตัวเลขในแต่ละช่อง ทำให้เราเห็นภาพรวมของความสัมพันธ์ระหว่างตัวแปรต่างๆ ได้อย่างชัดเจน เช่น ถ้าช่องระหว่าง Variable_A กับ Variable_B มีสีแดงเข้มและมีค่าใกล้ 1 แสดงว่าตัวแปรทั้งสองมีความสัมพันธ์เชิงบวกที่แข็งแกร่งนั่นเอง

เพื่อให้เห็นภาพชัดเจนยิ่งขึ้น เราจะใช้ตัวอย่างข้อมูลที่ใกล้เคียงกับสถานการณ์จริงมากขึ้น โดยจะยกตัวอย่างความสัมพันธ์ระหว่าง "เวลาที่ใช้ในการศึกษาต่อวัน (ชั่วโมง)" กับ "คะแนนสอบปลายภาค" และ "ความเครียด (คะแนนประเมิน)" ซึ่งน่าจะมีความสัมพันธ์กัน

สมมติฐาน

• เวลาที่ใช้ในการศึกษาต่อวัน มีความสัมพันธ์เชิงบวกกับคะแนนสอบ (ยิ่งศึกษามาก คะแนนน่าจะสูงขึ้น)
• เวลาที่ใช้ในการศึกษาต่อวัน อาจมีความสัมพันธ์เชิงบวกกับความเครียด (ยิ่งศึกษานาน อาจเครียดมากขึ้น)
• คะแนนสอบ อาจมีความสัมพันธ์เชิงลบกับความเครียด (ถ้าเครียดมาก คะแนนอาจจะลดลง)

**ข้อมูลตัวอย่าง (จำนวน 20 คน) **** ข้อมูลเหล่านี้เป็นเพียงตัวอย่างที่สร้างขึ้น เพื่อใช้ประกอบการอธิบาย

คน	เวลาศึกษา (ชม.)	คะแนนสอบ	ความเครียด (1-10)
1	2	65	5
2	3	70	6
3	5	80	7
4	1	55	4
5	4	75	6
6	6	90	8
7	2	60	5
8	3	72	7
9	5	85	7
10	1	50	3
11	4	78	6
12	7	92	9
13	2	62	4
14	3	68	6
15	5	82	8
16	1	52	3
17	4	76	7
18	6	88	7
19	2	63	5
20	3	71	6

เมื่อวิเคราะห์ผ่าน Python code

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

# สร้าง DataFrame จากข้อมูล
data = {
    'Study_Hours': [2, 3, 5, 1, 4, 6, 2, 3, 5, 1, 4, 7, 2, 3, 5, 1, 4, 6, 2, 3],
    'Exam_Score': [65, 70, 80, 55, 75, 90, 60, 72, 85, 50, 78, 92, 62, 68, 82, 52, 76, 88, 63, 71],
    'Stress_Level': [5, 6, 7, 4, 6, 8, 5, 7, 7, 3, 6, 9, 4, 6, 8, 3, 7, 7, 5, 6]
}
df = pd.DataFrame(data)

# คำนวณ Pearson Correlation Matrix
correlation_matrix_pearson = df.corr(method='pearson')

# แสดงผลด้วย Heatmap
plt.figure(figsize=(8, 6))
sns.heatmap(correlation_matrix_pearson, annot=True, cmap='coolwarm', fmt=".2f")
plt.title("Pearson Correlation Matrix (Study Hours, Exam Score, Stress Level)")
plt.show()

# คำนวณ Spearman Correlation Matrix
correlation_matrix_spearman = df.corr(method='spearman')

# แสดงผลด้วย Heatmap
plt.figure(figsize=(8, 6))
sns.heatmap(correlation_matrix_spearman, annot=True, cmap='coolwarm', fmt=".2f")
plt.title("Spearman Correlation Matrix (Study Hours, Exam Score, Stress Level)")
plt.show()

# ตัวอย่างการเข้าถึงค่าใน Correlation Matrix
print("\nCorrelation ระหว่าง Study_Hours กับ Exam_Score (Pearson):", correlation_matrix_pearson.loc['Study_Hours', 'Exam_Score'])
print("Correlation ระหว่าง Study_Hours กับ Stress_Level (Pearson):", correlation_matrix_pearson.loc['Study_Hours', 'Stress_Level'])
print("Correlation ระหว่าง Exam_Score กับ Stress_Level (Pearson):", correlation_matrix_pearson.loc['Exam_Score', 'Stress_Level'])

ผลลัพธ์

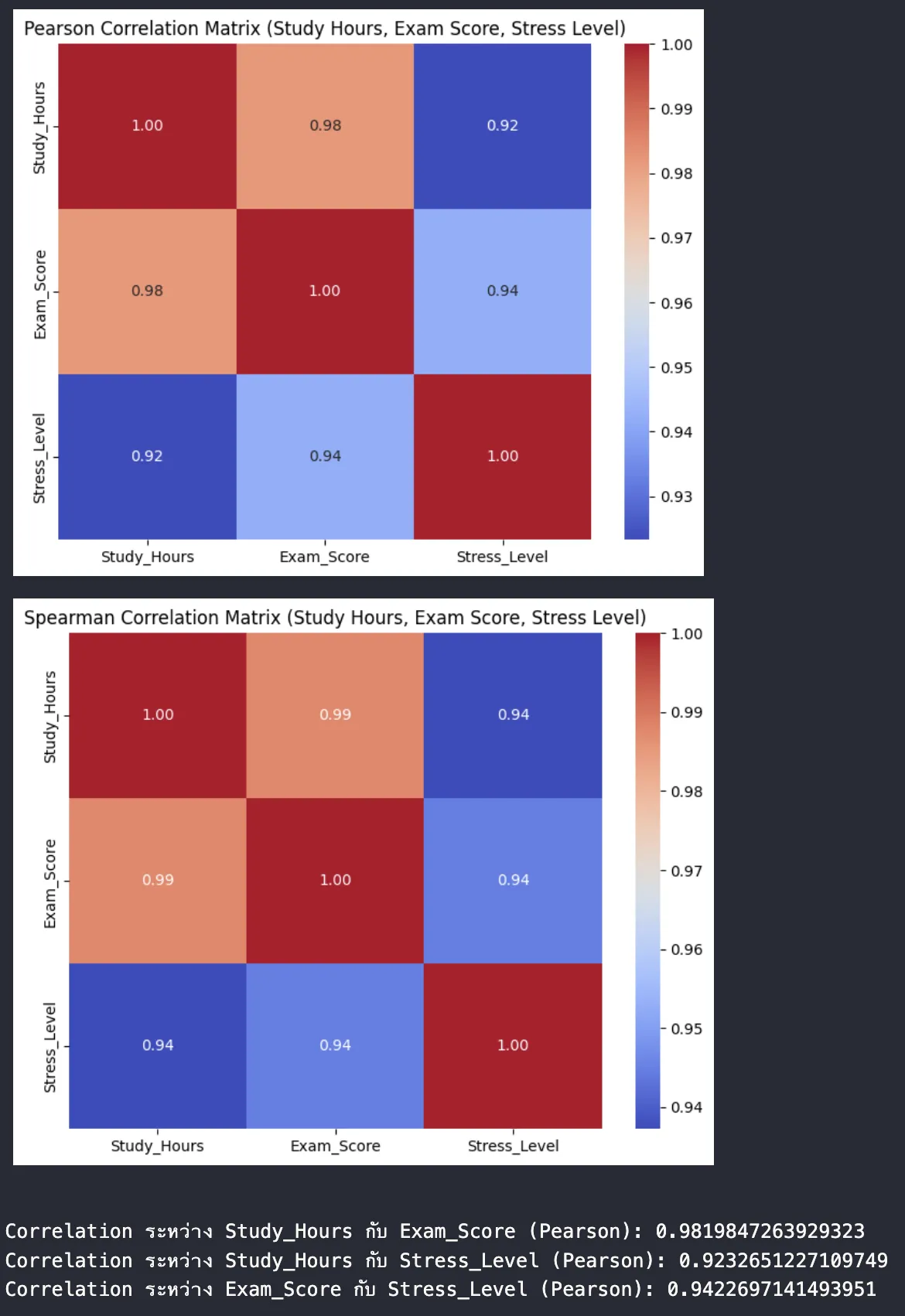
หลังจากรัน code เราจะเห็น Heatmap สองรูปและค่า correlation ที่แสดงออกมา โดยจาก Correlation Matrix เราสามารถตีความได้ลักษณะนี้

• สมมติว่าค่า Correlation ระหว่าง "Study_Hours" กับ "Exam_Score" ได้ประมาณ 0.95 แสดงว่ามีความสัมพันธ์เชิงบวกที่แข็งแกร่ง สอดคล้องกับสมมติฐาน
• สมมติว่าค่า Correlation ระหว่าง "Study_Hours" กับ "Stress_Level" ได้ประมาณ 0.7 แสดงว่ามีความสัมพันธ์เชิงบวกในระดับปานกลาง แสดงว่ายิ่งศึกษามาก มีแนวโน้มที่จะเครียดมากขึ้น
• สมมติว่าค่า Correlation ระหว่าง "Exam_Score" กับ "Stress_Level" ได้ประมาณ -0.6 แสดงว่ามีความสัมพันธ์เชิงลบในระดับปานกลาง แสดงว่ายิ่งเครียด คะแนนมีแนวโน้มลดลง

เป็นต้น

ข้อจำกัดของ Correlation Analysis

การวิเคราะห์ Correlation Analysis เป็นเครื่องมือทางสถิติที่มีประโยชน์ในการศึกษาความสัมพันธ์ระหว่างตัวแปรสองตัวหรือมากกว่า แต่ก็มีข้อจำกัดที่ควรพิจารณาอย่างถี่ถ้วน เพื่อหลีกเลี่ยงการตีความที่ผิดพลาด การทำความเข้าใจข้อจำกัดเหล่านี้เป็นสิ่งสำคัญอย่างยิ่งในการใช้การวิเคราะห์สหสัมพันธ์อย่างถูกต้องและมีประสิทธิภาพ โดยเฉพาะอย่างยิ่งประเด็นสำคัญสองประการคือ

1. ความสัมพันธ์ไม่แสดงถึงเหตุและผล (Correlation is not causation):

นี่เป็นข้อจำกัดที่สำคัญที่สุดของการวิเคราะห์ Correlation Analysis การที่ตัวแปรสองตัวมีความสัมพันธ์กัน (เช่น มีค่า Correlation สูง) “ไม่ได้หมายความว่าตัวแปรหนึ่งเป็นสาเหตุของอีกตัวแปรหนึ่ง” ตัวอย่างคลาสสิกที่มักถูกยกมาคือ ความสัมพันธ์ระหว่างยอดขายไอศกรีมและจำนวนการจมน้ำตายในช่วงฤดูร้อน พบว่าทั้งสองมีแนวโน้มเพิ่มขึ้นพร้อมกัน แต่ไม่ได้หมายความว่าการกินไอศกรีมทำให้คนจมน้ำตาย สาเหตุที่แท้จริงคือ อากาศร้อน ซึ่งเป็นตัวแปรกวน (Confounding Variable) ที่ส่งผลต่อทั้งสองตัวแปร

มีสถานการณ์ที่เป็นไปได้หลายแบบที่อธิบายความสัมพันธ์โดยไม่จำเป็นต้องเป็นเหตุและผลโดยตรง

• เหตุและผลโดยตรง (Direct Causation): A ทำให้เกิด B (เช่น การเรียนมากขึ้น ทำให้คะแนนสอบสูงขึ้น)
• เหตุและผลแบบผกผัน (Reverse Causation): B ทำให้เกิด A (เช่น คนที่ประสบความสำเร็จทางการเงิน มักจะได้รับการศึกษาที่ดี ซึ่งอาจเป็นเพราะความสำเร็จทางการเงินเอื้อให้ได้รับการศึกษาที่ดี)
• ตัวแปรกวน (Confounding Variable): C ทำให้เกิดทั้ง A และ B (เช่น อากาศร้อน ทำให้ทั้งยอดขายไอศกรีมและจำนวนการจมน้ำเพิ่มขึ้น)
• ความบังเอิญ (Coincidence): A และ B เปลี่ยนแปลงไปในทิศทางเดียวกันโดยบังเอิญ ไม่มีสาเหตุที่เชื่อมโยงกัน

ดังนั้น การวิเคราะห์สหสัมพันธ์เพียงอย่างเดียวไม่สามารถสรุปความเป็นเหตุและผลได้ หากต้องการศึกษาความเป็นเหตุและผล จำเป็นต้องใช้วิธีการวิเคราะห์ที่ซับซ้อนกว่า เช่น การทดลองแบบควบคุม (Controlled Experiment) หรือการวิเคราะห์ Regression ร่วมกับการควบคุมตัวแปรกวน เป็นต้น

2. การตีความค่าความสัมพันธ์ที่ไม่เหมาะสม

การตีความค่า Correlation ต้องระมัดระวัง เนื่องจากมีปัจจัยหลายอย่างที่อาจทำให้การตีความผิดพลาดได้ เช่น

• การตีความขนาดของความสัมพันธ์ (Magnitude of Correlation)
  • ค่า Correlation ที่สูง (ใกล้ +1 หรือ -1) ไม่ได้หมายความว่าความสัมพันธ์นั้น "สำคัญ" ในทางปฏิบัติ อาจเป็นเพียงความสัมพันธ์ที่แข็งแกร่งทางสถิติ แต่ไม่มีนัยสำคัญในบริบทจริง
  • ในทางกลับกัน ค่า Correlation ที่ต่ำ (ใกล้ 0) ไม่ได้หมายความว่าไม่มีความสัมพันธ์ อาจมีความสัมพันธ์แบบที่ไม่ใช่เชิงเส้น หรือมีความสัมพันธ์ที่อ่อนแอแต่มีความสำคัญในบริบทนั้น
• ข้อจำกัดของข้อมูล (Data Limitations)
  • Outliers (ค่าผิดปกติ): ค่าผิดปกติสามารถส่งผลกระทบอย่างมากต่อค่า Correlation ทำให้เกิดการตีความที่ผิดพลาด ควรตรวจสอบและจัดการกับค่าผิดปกติก่อนการวิเคราะห์
  • ข้อจำกัดของช่วงข้อมูล (Range Restriction): หากข้อมูลมีช่วงที่แคบ ค่า Correlation ที่คำนวณได้อาจต่ำกว่าความเป็นจริง เช่น หากศึกษาความสัมพันธ์ระหว่างความสูงและน้ำหนักในกลุ่มเด็กอายุ 5-10 ปี ค่า Correlation อาจต่ำกว่าการศึกษาในกลุ่มคนทุกช่วงอายุ
  • ข้อมูลที่ไม่เป็นเชิงเส้น (Non-linear Data): Pearson Correlation วัดเฉพาะความสัมพันธ์เชิงเส้น หากความสัมพันธ์เป็นแบบโค้ง Pearson Correlation อาจให้ผลลัพธ์ที่ผิดพลาด ควรพิจารณาใช้วิธีการวิเคราะห์อื่น เช่น Spearman Correlation หรือการแปลงข้อมูลให้เป็นเชิงเส้นก่อน
• การหา correlation โดยใช้ข้อมูล cross-sectional data ซึ่งเป็นการเก็บข้อมูล ณ จุดเวลาใดเวลาหนึ่ง ไม่สามารถใช้อธิบายการเปลี่ยนแปลงตามเวลาได้

ดังนั้นบทสรุปคือ

การวิเคราะห์ Correlation เป็นเครื่องมือที่มีประโยชน์ในการศึกษาความสัมพันธ์ระหว่างตัวแปร แต่ต้องใช้ด้วยความระมัดระวังและเข้าใจข้อจำกัด การตีความควรพิจารณาบริบทของข้อมูล ปัจจัยต่างๆ ที่อาจมีผลกระทบ และไม่สรุปความเป็นเหตุและผลจากการวิเคราะห์ Correlation เพียงอย่างเดียว

Regression Analysis

Regression Analysis คือ วิธีการทางสถิติที่ใช้ในการศึกษาความสัมพันธ์ระหว่างตัวแปรหนึ่งตัว ซึ่งเรียกว่าตัวแปรตาม (Dependent Variable หรือ Outcome Variable) กับตัวแปรอื่นๆ ตั้งแต่หนึ่งตัวขึ้นไป ซึ่งเรียกว่าตัวแปรอิสระ (Independent Variables หรือ Predictor Variables) โดยมีเป้าหมายเพื่อสร้างแบบจำลองทางคณิตศาสตร์ที่อธิบายความสัมพันธ์นี้ และใช้แบบจำลองนั้นในการทำนายหรืออธิบายค่าของตัวแปรตามเมื่อทราบค่าของตัวแปรอิสระ

จุดประสงค์หลักของการวิเคราะห์ Regression

• การอธิบาย (Explanation): เพื่อทำความเข้าใจว่าตัวแปรอิสระมีอิทธิพลต่อตัวแปรตามอย่างไร เช่น การศึกษาว่าปัจจัยด้านอายุ การศึกษา และรายได้ มีผลต่อความพึงพอใจในงานอย่างไร
• การทำนาย (Prediction): เพื่อทำนายค่าของตัวแปรตามจากค่าของตัวแปรอิสระ เช่น การทำนายยอดขายในอนาคตจากงบประมาณการโฆษณา และฤดูกาล
• การควบคุม (Control): เพื่อควบคุมหรือปรับปรุงค่าของตัวแปรตามโดยการเปลี่ยนแปลงค่าของตัวแปรอิสระ เช่น การปรับปรุงผลผลิตทางการเกษตรโดยการควบคุมปริมาณปุ๋ยและน้ำ

โดย ประเภทของการวิเคราะห์ Regression นั้นมีหลากหลายประเภท แต่จะขอหยิบ 3 ประเภทที่มีการพูดถึงบ่อยๆ และเป็นพื้นฐานแรกสุดที่ควรรู้นั่นคือ

1. Linear Regression ใช้เมื่อตัวแปรตามเป็นตัวแปรต่อเนื่อง และความสัมพันธ์ระหว่างตัวแปรตามและตัวแปรอิสระเป็นเชิงเส้น
2. Non-linear Regression ใช้เมื่อความสัมพันธ์ระหว่างตัวแปรตามและตัวแปรอิสระไม่เป็นเชิงเส้น เช่น ความสัมพันธ์แบบ exponential หรือ logarithmic
3. Logistic Regression ใช้เมื่อตัวแปรตามเป็นตัวแปรเชิงกลุ่ม (Categorical Variable) เช่น การทำนายว่าลูกค้าจะซื้อสินค้าหรือไม่ (ซื้อ/ไม่ซื้อ)

เพื่อให้เห็นภาพ เราจะขยายความ Regression ทั้ง 3 ตัวพร้อมตัวอย่างใน Python code ให้ทุกคนได้เห็นภาพไปพร้อมๆกัน

** ซึ่งเนื้อหานี้ จะมีการขยายผลไปยังส่วนของ Machine Learning ด้วยนะครับ เพราะจะเป็นไอเดียสำคัญที่ทำให้ Machine Learning สามารถ “Learning” ได้

Linear Regression

Linear Regression คือ วิธีการทางสถิติที่ใช้ในการหาความสัมพันธ์เชิงเส้นระหว่างตัวแปรสองกลุ่ม คือ ตัวแปรต้นหรือตัวแปรอิสระ (Independent Variable หรือ Predictor Variable) และตัวแปรตาม (Dependent Variable หรือ Outcome Variable) โดยมีสมการเส้นตรงเป็นตัวแทนความสัมพันธ์นั้น และใช้สมการนั้นในการทำนายค่าของตัวแปรตามเมื่อทราบค่าตัวแปรต้น

โดย Linear Regression จะพยายามหารูปแบบความสัมพันธ์แบบเส้นตรงที่ดีที่สุดระหว่างตัวแปรต้นและตัวแปรตาม โดยเส้นตรงนี้จะเรียกว่า "Regression Line" หรือ "เส้นแนวโน้มที่ดีที่สุด (Best-Fit Line)" ซึ่งสามารถแทนด้วยสมการ

• Simple Linear Regression (ตัวแปรต้น 1 ตัว): $y = mx + b$
• Multiple Linear Regression (ตัวแปรต้นมากกว่า 1 ตัว): $y = b_0 + b_1x_1 + b_2x_2 + \dots + b_nx_n$

โดยที่

• y คือ ตัวแปรตาม (ค่าที่เราต้องการทำนาย)
• x หรือ $x_i$ คือ ตัวแปรต้น
• m หรือ $b_0 + b_1x_1 + b_2x_2 + \dots + b_nx_n$ คือ สัมประสิทธิ์ความชัน (Slope หรือ Coefficient) แสดงถึงการเปลี่ยนแปลงของ y เมื่อ x เปลี่ยนแปลงไป 1 หน่วย
• b หรือ $b_0$ คือ จุดตัดแกน y (Intercept) แสดงถึงค่า y เมื่อ x เป็น 0

โดย วิธีการคำนวณหาค่า m และ b ที่นิยมใช้คือ วิธี Least Squares (กำลังสองน้อยที่สุด) โดยมีหลักการคือ การหาเส้นตรงที่ทำให้ผลรวมของกำลังสองของระยะห่างระหว่างจุดข้อมูลจริงกับเส้นตรงมีค่าน้อยที่สุด

สำหรับ Simple Linear Regression สามารถคำนวณ m และ b ได้ดังนี้

$$m = \frac{\sum \left( (x_i - \bar{x})(y_i - \bar{y}) \right)}{\sum \left( (x_i - \bar{x})^2 \right)}$$ $$b = \bar{y} - m \bar{x}$$

โดยที่

• $x_i$ และ $y_i$ คือ ค่าของตัวแปรต้นและตัวแปรตามของข้อมูลแต่ละชุด
• x̄ และ ȳ คือ ค่าเฉลี่ยของตัวแปรต้นและตัวแปรตาม

(สำหรับ Multiple Linear Regression การคำนวณจะซับซ้อนกว่า และมักใช้ software ทางสถิติช่วยในการคำนวณ เช่น python เองก็สามารถทำได้เช่นกัน)

ตัวอย่างการคำนวณ (Simple Linear Regression)

สมมติเราต้องการศึกษาความสัมพันธ์ระหว่าง "จำนวนชั่วโมงที่อ่านหนังสือ (x)" กับ "คะแนนสอบ (y)" โดยเก็บข้อมูลนักเรียน 5 คน

นักเรียน	จำนวนชั่วโมงอ่านหนังสือ (x)	คะแนนสอบ (y)
1	1	50
2	2	60
3	3	75
4	4	80
5	5	95

1. คำนวณค่าเฉลี่ย x̄ และ ȳ
   • x̄ = (1 + 2 + 3 + 4 + 5) / 5 = 3
   • ȳ = (50 + 60 + 75 + 80 + 95) / 5 = 72
2. คำนวณ Σ[(xi - x̄)(yi - ȳ)]
   • (1-3)(50-72) + (2-3)(60-72) + (3-3)(75-72) + (4-3)(80-72) + (5-3)(95-72)
   • (-2)(-22) + (-1)(-12) + (0)(3) + (1)(8) + (2)(23)
   • 44 + 12 + 0 + 8 + 46 = 110
3. คำนวณ Σ[(xi - x̄)²]
   • (1-3)² + (2-3)² + (3-3)² + (4-3)² + (5-3)²
   • 4 + 1 + 0 + 1 + 4 = 10
4. คำนวณ m
   • m = 110 / 10 = 11
5. คำนวณ b
   • b = 72 - (11 * 3) = 72 - 33 = 39

ดังนั้น สมการ Linear Regression คือ $y = 11x + 39$ หมายความว่าทุกๆ ชั่วโมงที่อ่านหนังสือเพิ่มขึ้น คะแนนสอบจะเพิ่มขึ้นประมาณ 11 คะแนน โดยมีคะแนนเริ่มต้นประมาณ 39 คะแนน

สำหรับ Python code การคำนวนก็จะสามารถคำนวนได้จาก sklearn.linear_model ของ library Scikit Learn

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

# ข้อมูล
x = np.array([1, 2, 3, 4, 5]).reshape((-1, 1))  # Reshape ให้เป็น matrix (สำคัญสำหรับ sklearn)
y = np.array([50, 60, 75, 80, 95])

# สร้างและ fit โมเดล
model = LinearRegression().fit(x, y)

# ค่าสัมประสิทธิ์และจุดตัด
r_sq = model.score(x, y) #ค่า R-square
print(f"coefficient of determination: {r_sq}")
print(f"intercept: {model.intercept_}")
print(f"coefficients: {model.coef_}")

# ทำนายค่า
y_pred = model.predict(x)
print(f"predicted response:\n{y_pred}")

#  plot กราฟ
plt.scatter(x, y, color="blue", label="Actual data")
plt.plot(x, y_pred, color="red", label="Linear regression")
plt.xlabel("Study Hours")
plt.ylabel("Exam Score")
plt.legend()
plt.show()

ผลลัพธ์

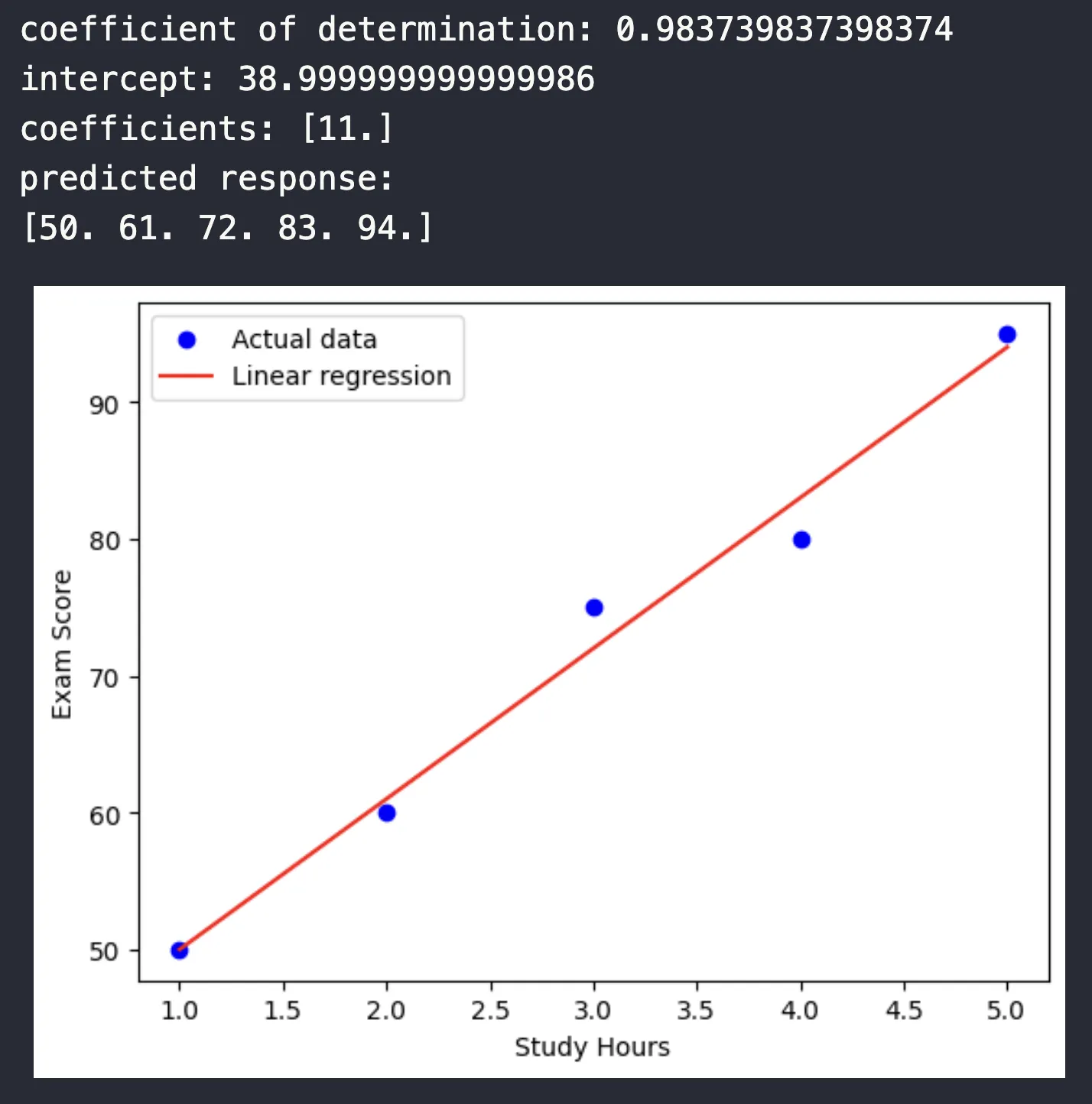
สังเกตว่าพอเป็น python code จะมี library คำนวนมาให้เสร็จซับแล้ว เราเพียงทำความเข้าใจในคำสั่งก็จะสามารถหาค่าสัมประสิทธิ์ coefficience, จุดตัด intercept พร้อมกับ plot graph ดูความสัมพันธ์ได้

ข้อควรระวัง

• Linear Regression เหมาะกับข้อมูลที่มีความสัมพันธ์เชิงเส้น หากข้อมูลมีความสัมพันธ์แบบอื่น (เช่น โค้ง) ควรพิจารณาใช้วิธีอื่น เช่น Polynomial Regression
• Correlation ไม่ได้หมายถึง Causation (เหตุและผล) การที่ตัวแปรสองตัวมีความสัมพันธ์กันไม่ได้หมายความว่าตัวแปรหนึ่งเป็นสาเหตุของอีกตัวแปรหนึ่ง
• ควรตรวจสอบข้อสมมติของ Linear Regression ก่อนการใช้งาน เช่น ความเป็นอิสระของค่าคลาดเคลื่อน การแจกแจงแบบปกติของค่าคลาดเคลื่อน และความแปรปรวนคงที่ของค่าคลาดเคลื่อน

Non-linear Regression

Non-linear Regression คือ วิธีการทางสถิติที่ใช้ในการหาความสัมพันธ์ระหว่างตัวแปรต้น (Independent Variable) และตัวแปรตาม (Dependent Variable) ในกรณีที่ความสัมพันธ์นั้น ไม่สามารถอธิบายได้ด้วยเส้นตรง ต่างจากการวิเคราะห์ Linear Regression ที่ใช้เส้นตรงในการอธิบายความสัมพันธ์

ใน Non-linear Regression ความสัมพันธ์ระหว่างตัวแปรจะถูกแทนด้วย function ที่ไม่ใช่เส้นตรง เช่น function exponential, logarithmic, polynomial หรือ sigmoid ซึ่งมีความซับซ้อนกว่าสมการเส้นตรง y = mx + b

โดยความแตกต่างจาก Linear Regression คือ

• รูปแบบความสัมพันธ์: Linear Regression อธิบายความสัมพันธ์ด้วยเส้นตรง ในขณะที่ Non-linear Regression อธิบายด้วยเส้นโค้งหรือรูปแบบอื่นๆ ที่ไม่ใช่เส้นตรง
• สมการ: Linear Regression ใช้สมการ y = mx + b หรือ y = b0 + b1x1 + b2x2 + ... ส่วน Non-linear Regression ใช้สมการที่มีรูปแบบที่หลากหลายกว่า เช่น y = ax² + bx + c (quadratic), y = ae^(bx) (exponential)
• การคำนวณ: การคำนวณใน Linear Regression ค่อนข้างตรงไปตรงมา โดยใช้วิธี Least Squares ในการหาค่าสัมประสิทธิ์ ในขณะที่ Non-linear Regression มักใช้วิธีการทำซ้ำ (iterative methods) เช่น Gradient Descent หรือ Gauss-Newton เพื่อหาค่า parameters ที่เหมาะสม

ดังนั้น การคำนวณใน Non-linear Regression ค่อนข้างซับซ้อนและไม่มีสูตรตายตัวเหมือน Linear Regression เนื่องจากต้องใช้วิธีการวนซ้ำเพื่อหาค่า parameters ที่ทำให้แบบจำลองเหมาะสมกับข้อมูลมากที่สุด หลักการคือพยายามลดค่าความแตกต่างระหว่างค่าที่ทำนายได้จากแบบจำลองกับค่าจริงของข้อมูล โดยใช้วิธีการต่างๆ เช่น

• Iterative Methods: เช่น Gradient Descent, Gauss-Newton, Levenberg-Marquardt algorithm ซึ่งเป็นวิธีการหาค่าที่เหมาะสมโดยการปรับค่า parameters ไปเรื่อยๆ จนกว่าจะเข้าใกล้ค่าที่ดีที่สุด
• Linearization: ในบางกรณี สามารถแปลงสมการ Non-linear ให้เป็น Linear ได้โดยการแปลงข้อมูล เช่น การใช้ logarithm แล้วจึงใช้วิธี Linear Regression

ตัวอย่างสมการ Non-linear

• Exponential: $y = a * \exp(bx)$
• Logarithmic: $y = a + b * ln(x)$
• Power: $y = ax^b$
• Sigmoid: $y = \frac{1}{1 + \exp(-x)}$

ตัวอย่างการคำนวณ (เชิงไอเดีย)

สมมติเรามีข้อมูลความสัมพันธ์ระหว่างเวลา (x) และจำนวนแบคทีเรีย (y) ที่เติบโตแบบ exponential ข้อมูลประมาณนี้

เวลา (x)	จำนวนแบคทีเรีย (y)
0	1
1	2.7
2	7.4
3	20.1

สมการที่เราคิดว่าเหมาะสมคือ $y = e^x$ (ซึ่งเป็นกรณีพิเศษของ $y = a * exp(bx)$ โดย a=1 และ b=1)

ในทางปฏิบัติ เราจะใช้วิธี iterative ในการหาค่า a และ b ที่ดีที่สุด โดยโปรแกรมจะเริ่มต้นด้วยค่าประมาณของ a และ b แล้วทำการปรับค่าเหล่านี้ไปเรื่อยๆ จนกว่าจะได้ค่าที่ทำให้ผลรวมของกำลังสองของความแตกต่างระหว่างค่า y ที่ทำนายได้จากสมการกับค่า y จริงน้อยที่สุด

ซึ่งในเคสลักษณะนี้ เราสามารถใช้ software สถิติอย่าง python code ในการช่วยคำนวนได้ เช่น code นี้

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

# ข้อมูล
x_data = np.array([0, 1, 2, 3])
y_data = np.array([1, 2.7, 7.4, 20.1])

#  function  exponential
def func(x, a, b):
    return a * np.exp(b * x)

# Curve fitting
popt, pcov = curve_fit(func, x_data, y_data)

# ค่า parameter ที่ได้
a = popt[0]
b = popt[1]

print(f"a = {a}, b = {b}")

# สร้างค่า y ที่ทำนายได้
y_pred = func(x_data, a, b)

#  plot กราฟ
plt.plot(x_data, y_data, 'o', label='data')
plt.plot(x_data, y_pred, '-', label='fit')
plt.legend()
plt.show()

ผลลัพธ์

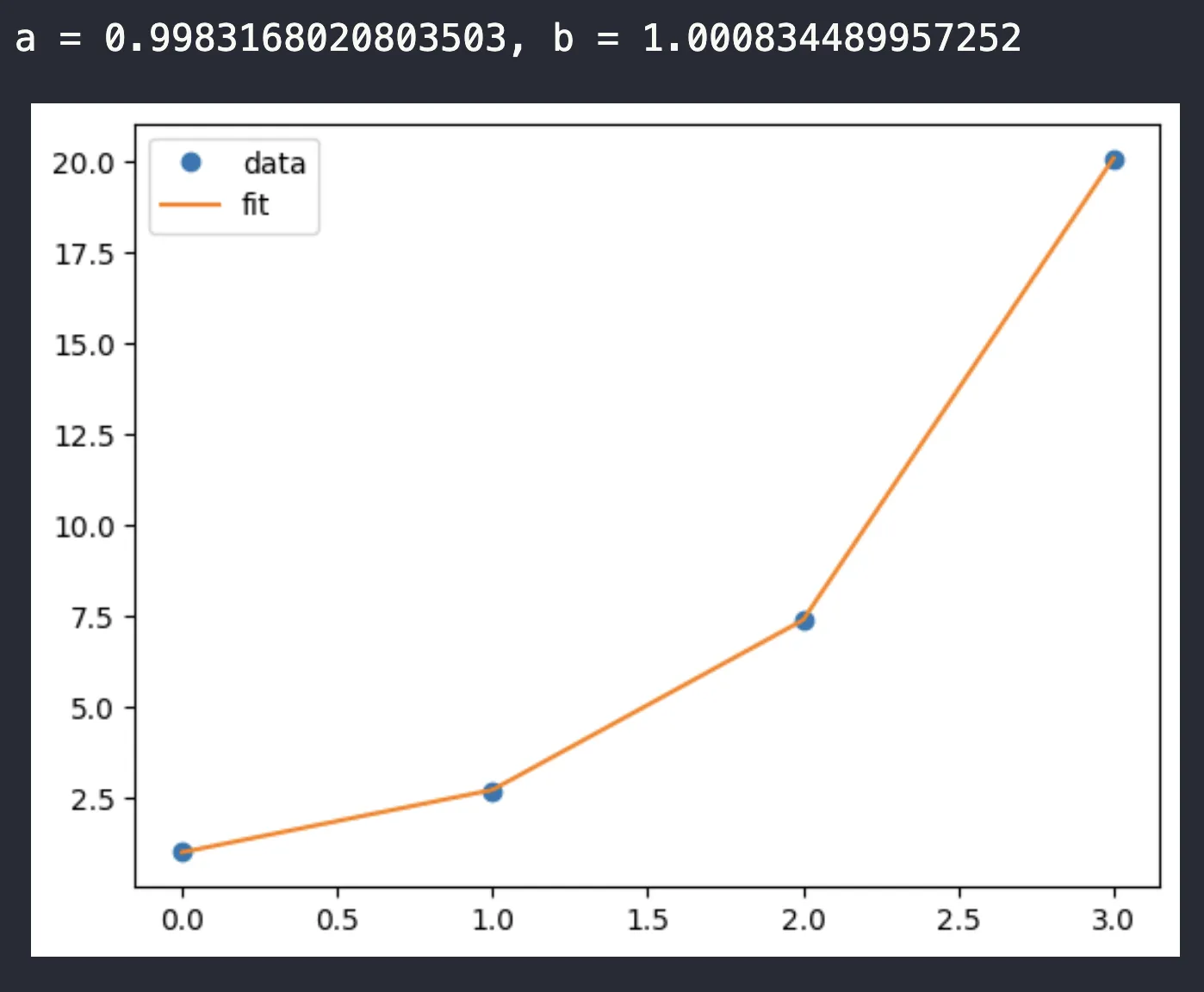
Note

• ใช้ scipy.optimize.curve_fit ในการหาค่า a และ b โดย
• เริ่มต้นจากการกำหนด function ทางคณิตศาสตร์ที่คิดว่าเหมาะสมกับข้อมูล โดยในโค้ดตัวอย่าง function คือ func(x, a, b) = a * np.exp(b * x) ซึ่งเป็น function exponential function นี้รับค่า x และ parameter a และ b เป็นอินพุต และคืนค่า y ที่คำนวณได้
• function curve_fit ใช้หลักการของ "Least Squares" (กำลังสองน้อยที่สุด) ในการหาค่า a และ b โดยมีขั้นตอนการทำงานดังนี้
  • เริ่มต้นด้วยค่าประมาณ: ในทางปฏิบัติ curve_fit จะเริ่มต้นด้วยค่าประมาณของ a และ b (ถ้าไม่ได้กำหนด ค่าเริ่มต้นให้ function จะใช้ค่าเริ่มต้นโดยอัตโนมัติ)
  • การวนซ้ำ (Iteration): function จะทำการวนซ้ำเพื่อปรับค่า a และ b ไปเรื่อยๆ โดยในแต่ละรอบของการวนซ้ำ จะคำนวณค่า y ที่ทำนายได้จาก function func โดยใช้ค่า a และ b ในปัจจุบัน
  • การคำนวณความแตกต่าง: function จะคำนวณหาความแตกต่างระหว่างค่า y ที่ทำนายได้ กับค่า y จริงจากข้อมูล (y_data)
  • การปรับค่า parameter : function จะปรับค่า a และ b เพื่อลดผลรวมของกำลังสองของความแตกต่างเหล่านี้ ซึ่งก็คือพยายามหารูปแบบความสัมพันธ์ที่ทำให้เส้นโค้งที่สร้างจาก function เข้าใกล้จุดข้อมูลมากที่สุด
  • การลู่เข้า (Convergence): ขั้นตอนที่ 2-4 ที่กล่าวมา จะทำซ้ำไปเรื่อยๆ จนกว่าค่า a และ b จะลู่เข้าสู่ค่าที่เหมาะสม หรือจนกว่าจะถึงจำนวนรอบที่กำหนดไว้
• ท้ายที่สุดก็จะได้ค่าประมาณ a, b ที่ดีที่สุดจาก curve_fit ออกมาได้

ข้อควรระวัง

• การเลือก function ที่เหมาะสมเป็นสิ่งสำคัญ ควรพิจารณาลักษณะของข้อมูลและทฤษฎีที่เกี่ยวข้อง
• Non-linear Regression อาจมีปัญหา convergence (การลู่เข้า) คือวิธีการ iterative อาจไม่สามารถหาค่าที่เหมาะสมได้ ขึ้นอยู่กับค่าเริ่มต้นของ parameter และลักษณะของข้อมูล
• การตีความผลลัพธ์ควรระมัดระวัง และพิจารณาบริบทของปัญหาด้วย

Logistic Regression

Logistic Regression คือ วิธีการทางสถิติที่ใช้ในการวิเคราะห์ความสัมพันธ์ระหว่างตัวแปรอิสระ (Independent Variables) กับตัวแปรตาม (Dependent Variable) ที่มีลักษณะเป็น เชิงกลุ่ม (Categorical) หรือ Binary เช่น สำเร็จ/ไม่สำเร็จ, ใช่/ไม่ใช่, มี/ไม่มี โดยมีเป้าหมายเพื่อทำนายความน่าจะเป็นที่เหตุการณ์หนึ่งจะเกิดขึ้น

ความแตกต่างจาก Linear Regression

• ตัวแปรตาม: Linear Regression ใช้กับตัวแปรตามที่เป็นตัวเลขต่อเนื่อง ในขณะที่ Logistic Regression ใช้กับตัวแปรตามที่เป็นกลุ่ม
• ผลลัพธ์: Linear Regression ทำนายค่าตัวเลข ในขณะที่ Logistic Regression ทำนายความน่าจะเป็น (ระหว่าง 0 ถึง 1)
• สมการ: Logistic Regression ใช้ function Sigmoid หรือ Logistic ในการแปลงผลรวมเชิงเส้นของตัวแปรอิสระให้อยู่ในรูปความน่าจะเป็น

function Sigmoid (Logistic Function) จะมีหน้าตาแบบนี้

$$P(Y=1) = \frac{1}{1 + e^{-z}}$$

โดยที่

• P(Y=1) คือ ความน่าจะเป็นที่ตัวแปรตาม Y จะมีค่าเป็น 1 (เช่น สำเร็จ, ใช่)
• e คือ ค่าคงที่ของออยเลอร์ (ประมาณ 2.718)
• z คือ ผลรวมเชิงเส้นของตัวแปรอิสระ ซึ่งมีรูปแบบคล้ายกับ Linear Regression
  • $b_0$ คือ จุดตัดแกน (intercept)
  • $b_1, b_2, ..., b_n$ คือ สัมประสิทธิ์ (coefficients) ของตัวแปรอิสระ $x_1, x_2, ..., x_n$

$$z = b_0 + b_1x_1 + b_2x_2 + \dots + b_nx_n$$

โดยการตีความผลลัพธ์นั้น สามารถทำได้ดังนี้

ค่า P(Y=1) ที่ได้จาก function Sigmoid จะอยู่ระหว่าง 0 ถึง 1 ซึ่งสามารถตีความได้ว่า

• P(Y=1) > 0.5: มีแนวโน้มที่เหตุการณ์ Y=1 จะเกิดขึ้น
• P(Y=1) < 0.5: มีแนวโน้มที่เหตุการณ์ Y=0 จะเกิดขึ้น

โดยทั่วไป มักจะกำหนดค่า Threshold (เช่น 0.5) เพื่อแบ่งกลุ่ม หาก P(Y=1) มากกว่า Threshold จะจัดอยู่ในกลุ่ม 1 และหากน้อยกว่าจะจัดอยู่ในกลุ่ม 0

ที่นี้แล้ว วิธีการคำนวณหาค่าสัมประสิทธิ์ $(b_0, b_1, ... b_n)$ ละสามารถคำนวนได้อย่างไร ?

การคำนวณหาค่าสัมประสิทธิ์ใน Logistic Regression ไม่ได้ใช้วิธี Least Squares เหมือน Linear Regression แต่ใช้วิธี Maximum Likelihood Estimation (MLE) ซึ่งเป็นวิธีการหาค่า parameter ที่ทำให้ความน่าจะเป็นที่จะได้ข้อมูลที่สังเกตเห็นมีค่ามากที่สุด (ส่วนใหญ่ก็จะใช้ software คำนวนมากกว่าคำนวนด้วยมือ)

เรามาลองดูตัวอย่างเพื่อเพิ่มความเข้าใจกัน

สมมติเราต้องการศึกษาว่า "จำนวนชั่วโมงที่ใช้ในการเรียนพิเศษ (x)" มีผลต่อ "การสอบผ่าน/ไม่ผ่าน (y)" โดยเก็บข้อมูลนักเรียน ตามนี้

นักเรียน	จำนวนชั่วโมงเรียนพิเศษ (x)	สอบผ่าน (y)
1	1	0 (ไม่ผ่าน)
2	2	0 (ไม่ผ่าน)
3	3	1 (ผ่าน)
4	4	1 (ผ่าน)
5	5	1 (ผ่าน)

เมื่อใช้ Logistic Regression เราอาจได้สมการ เช่น

$$P(\text{สอบผ่าน}) = \frac{1}{1 + e^{-(-3 + 1 \cdot x)}}$$

หากนักเรียนเรียนพิเศษ 4 ชั่วโมง

$$P(\text{สอบผ่าน}) = \frac{1}{1 + e^{-(-3 + 1 \cdot 4)}} = \frac{1}{1 + e^{-1}} \approx 0.73$$

แสดงว่านักเรียนคนนี้ (ที่เรียนพิเศษ 4 ชั่วโมง) มีความน่าจะเป็นที่จะสอบผ่านประมาณ 73%

เมื่อลองคำนวนสิ่งนี้ด้วย code python ด้านล่างนี้ (ตัวอย่างนี้เป็นตัวอย่างของการทำ Machine Learning แล้ว)

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report, confusion_matrix

# สร้างข้อมูลตัวอย่าง
data = {'hours': [0.5, 0.75, 1.0, 1.25, 1.5, 1.75, 1.75, 2.0, 2.25, 2.5, 2.75, 3.0, 3.25, 3.5, 4.0, 4.25, 4.5, 4.75, 5.0, 5.5],
        'pass': [0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1]}
df = pd.DataFrame(data)

# แบ่งข้อมูลเป็น training set และ test set
X = df[['hours']]
y = df['pass']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

# สร้างและ train โมเดล Logistic Regression
logreg = LogisticRegression()
logreg.fit(X_train, y_train)

# ทำนายผลบน test set
y_pred = logreg.predict(X_test)

# ประเมินผลโมเดล
print(confusion_matrix(y_test, y_pred))
print(classification_report(y_test, y_pred))

# แสดงค่าสัมประสิทธิ์และ intercept
print('Intercept: \n', logreg.intercept_)
print('Coefficients: \n', logreg.coef_)

# plot กราฟ
plt.scatter(X,y)
plt.plot(X, logreg.predict_proba(X)[:, 1], color='red')
plt.xlabel("Hours")
plt.ylabel("Probability to Pass")
plt.show()

จาก code ชุดนี้ สิ่งที่ code ทำคือ

• สร้าง DataFrame จาก data ที่มีจำนวนชั่วโมงเรียนพิเศษ (hours) และผลสอบ (pass)
• แบ่งข้อมูลออกเป็นส่วนสำหรับฝึกฝน (training set) และส่วนสำหรับทดสอบ (test set) โดยใช้ train_test_split แบ่ง 30% สำหรับทดสอบ
• สร้างโมเดล Logistic Regression โดยใช้ LogisticRegression() จาก scikit-learn
• ฝึกฝนโมเดล (fit) โดยใช้ข้อมูลฝึกฝน (X_train, y_train)
  • ใน Logistic Regression fit จะใช้วิธีการ optimization (เช่น Gradient Descent) เพื่อหาค่าสัมประสิทธิ์ (coefficients) ที่เหมาะสม โดยอิงจากหลักการของ MLE เพื่อ maximize Likelihood
  • fit เป็น การนำหลักการ ต่างๆ มาใช้ในการฝึกฝนโมเดล ซึ่ง MLE เป็นหนึ่งในหลักการเหล่านั้น
• ทำนายผลลัพธ์บนข้อมูลทดสอบ (X_test) และเก็บผลลัพธ์ใน y_pred
• แสดงผล Confusion Matrix เพื่อดูการเปรียบเทียบระหว่างผลทำนายและผลจริง
• แสดง Classification Report ซึ่งประกอบด้วยค่า precision, recall, f1-score และ support เพื่อประเมินประสิทธิภาพของโมเดล
• แสดงค่า Intercept ($b_0$) และ Coefficients ($b_1$) ของสมการ Logistic Regression และ plot กราฟ Scatter plot แสดงข้อมูลดิบ และ plot กราฟเส้นแสดงความน่าจะเป็นที่ทำนายได้โดยโมเดล Logistic Regression โดยแกน x คือจำนวนชั่วโมง และแกน y คือความน่าจะเป็นที่จะสอบผ่าน

ผลลัพธ์

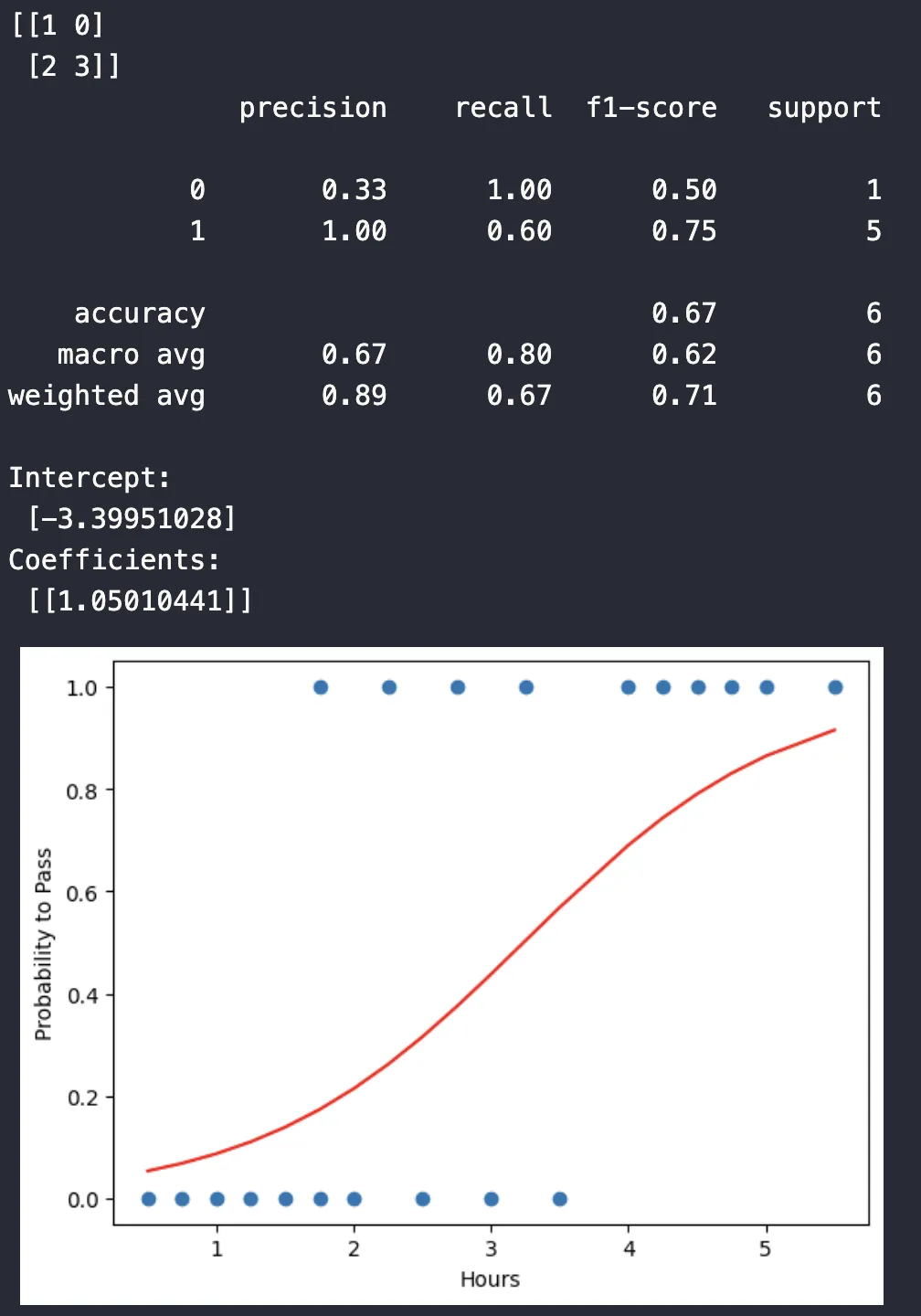
จาก code Python ชุดนี้ ผลลัพธ์ที่ได้จากโค้ดชุดนี้สามารถตีความได้ดังนี้

1. Confusion Matrix แสดงผลการทำนายเทียบกับผลลัพธ์จริงในรูปแบบตาราง

[[TN  FP]
 [FN  TP]]

โดยที่:

• TN (True Negative): จำนวนครั้งที่ทำนายว่า ไม่ผ่าน และ ไม่ผ่าน จริงๆ
• FP (False Positive): จำนวนครั้งที่ทำนายว่า ผ่าน แต่ ไม่ผ่าน จริงๆ (Type I error)
• FN (False Negative): จำนวนครั้งที่ทำนายว่า ไม่ผ่าน แต่ ผ่าน จริงๆ (Type II error)
• TP (True Positive): จำนวนครั้งที่ทำนายว่า ผ่าน และ ผ่าน จริงๆ

ตัวอย่างเช่น ถ้า Confusion Matrix คือ [[1, 0], [2, 3]] หมายความว่า:

• มี 1 คนที่ทำนายว่าไม่ผ่านและไม่ผ่านจริง
• มี 0 คนที่ทำนายว่าผ่านแต่ไม่ผ่านจริง
• มี 2 คนที่ทำนายว่าไม่ผ่านแต่ผ่านจริง
• มี 3 คนที่ทำนายว่าผ่านและผ่านจริง

2. Classification Report ให้ข้อมูลเพิ่มเติมเกี่ยวกับประสิทธิภาพของโมเดล

              precision    recall  f1-score   support

           0       x.xx      x.xx      x.xx        N0
           1       x.xx      x.xx      x.xx        N1

    accuracy                           x.xx        N
   macro avg       x.xx      x.xx      x.xx        N
weighted avg       x.xx      x.xx      x.xx        N

โดยที่

• Precision: ความแม่นยำในการทำนายผลบวก (ผ่าน) คือ จากคนที่ทำนายว่าผ่าน มีกี่คนที่ผ่านจริง (TP / (TP + FP))
• Recall (Sensitivity): ความสามารถในการหาผลบวกทั้งหมด คือ จากคนที่ผ่านจริง ทำนายได้ถูกต้องกี่คน (TP / (TP + FN))
• F1-score: ค่าเฉลี่ย Harmonic Mean ของ Precision และ Recall ใช้ประเมินความสมดุลระหว่างสองค่านี้ (2 * (Precision * Recall) / (Precision + Recall))
• Support: จำนวนข้อมูลจริงในแต่ละคลาส (0 = ไม่ผ่าน, 1 = ผ่าน)
• Accuracy: ความแม่นยำโดยรวมของโมเดล (TP + TN) / (TP + TN + FP + FN)
• macro avg: ค่าเฉลี่ยของ precision, recall, f1-score โดยไม่คำนึงถึงจำนวนข้อมูลในแต่ละคลาส
• weighted avg: ค่าเฉลี่ยของ precision, recall, f1-score โดยคำนึงถึงจำนวนข้อมูลในแต่ละคลาส

ค่า x.xx แทนด้วยตัวเลขที่คำนวณได้จากข้อมูล และ N0, N1 และ N แทนจำนวนข้อมูลในแต่ละกลุ่ม

เช่นตัวอย่างจากผลลัพธ์นี้

              precision    recall  f1-score   support

           0       0.33      1.00      0.50         1
           1       1.00      0.60      0.75         5

    accuracy                           0.67         6
   macro avg       0.67      0.80      0.62         6
weighted avg       0.89      0.67      0.71         6

ก็จะตีความได้โดยประมาณว่ามีความแม่นยำราวๆ 67%

3. Intercept และ Coefficients

• Intercept ($b_0$): คือ ค่าคงที่ในสมการ Logistic Regression เป็นค่า log-odds ของการสอบผ่านเมื่อจำนวนชั่วโมงเรียนพิเศษเป็น 0 (ในทางปฏิบัติอาจไม่มีความหมายมากนัก เพราะไม่มีใครเรียน 0 ชั่วโมง)
• Coefficients ($b_1$): คือ ค่าที่แสดงถึงผลกระทบของตัวแปรอิสระ (จำนวนชั่วโมงเรียนพิเศษ) ต่อ log-odds ของการสอบผ่าน ค่าบวกหมายความว่า ยิ่งเรียนพิเศษมาก โอกาสสอบผ่านก็ยิ่งมากขึ้น

จากค่า Intercept และ Coefficients เราสามารถสร้างสมการ Logistic Regression ได้ (ก็จะเหมือนกับตัวอย่างที่เรายกในตอนแรกสุด)

$$P(\text{สอบผ่าน}) = \frac{1}{1 + e^{-(b_0 + b_1 \cdot \text{จำนวนชั่วโมงเรียนพิเศษ})}}$$

ข้อควรระวัง

• ควรมีข้อมูลเพียงพอเพื่อให้โมเดลเรียนรู้ได้อย่างมีประสิทธิภาพ
• ควรตรวจสอบความสัมพันธ์ระหว่างตัวแปรอิสระและตัวแปรตามก่อนใช้ Logistic Regression
• ควรระวังปัญหา multicollinearity (ความสัมพันธ์กันเองระหว่างตัวแปรอิสระ)

การวัดคุณภาพของ Model Regression

การวัดคุณภาพของ Model Regression คือการประเมินว่าโมเดลที่สร้างขึ้นสามารถทำนายค่าได้อย่างแม่นยำเพียงใด ซึ่งมีความสำคัญอย่างยิ่งในการเลือกโมเดลที่ดีที่สุดสำหรับงานนั้นๆ โดยทั่วไปแล้ว เราจะวัดจากความแตกต่างระหว่างค่าที่โมเดลทำนาย (predicted values) กับค่าจริง (actual values) ยิ่งความแตกต่างน้อยเท่าไหร่ โมเดลก็จะยิ่งแม่นยำมากขึ้น

วิธีการวัดคุณภาพของ Model Regression ต่อไปนี้ จะเป็นวิธีที่มักจะเป็นที่นิยมใช้กันได้แค่

1. Mean Absolute Error (MAE) หรือ ค่าเฉลี่ยความผิดพลาดสัมบูรณ์ คือค่าเฉลี่ยของความแตกต่างสัมบูรณ์ระหว่างค่าที่ทำนายกับค่าจริง

$$\text{MAE} = \frac{1}{n} \sum \left| y_i - \hat{y}_i \right|$$

โดยที่

• n คือ จำนวนข้อมูลทั้งหมด
• yᵢ คือ ค่าจริงของข้อมูลตัวที่ i
• ŷᵢ คือ ค่าที่โมเดลทำนายของข้อมูลตัวที่ i
• | | คือ ค่าสัมบูรณ์

2. Mean Squared Error (MSE) หรือ ค่าเฉลี่ยความผิดพลาดกำลังสอง คือค่าเฉลี่ยของความแตกต่างระหว่างค่าที่ทำนายกับค่าจริง ยกกำลังสอง

$$\text{MSE} = \frac{1}{n} \sum (y_i - \hat{y}_i)^2$$

โดยที่

• n คือ จำนวนข้อมูลทั้งหมด
• yᵢ คือ ค่าจริงของข้อมูลตัวที่ i
• ŷᵢ คือ ค่าที่โมเดลทำนายของข้อมูลตัวที่ i

3. Root Mean Squared Error (RMSE) หรือ รากที่สองของค่าเฉลี่ยความผิดพลาดกำลังสอง คือรากที่สองของ MSE ทำให้หน่วยของ RMSE กลับมาเป็นหน่วยเดียวกับตัวแปรที่เราต้องการทำนาย ทำให้ง่ายต่อการตีความ

$$\text{RMSE} = \sqrt{\text{MSE}} = \sqrt{\frac{1}{n} \sum (y_i - \hat{y}_i)^2}$$

โดยที่

• n คือ จำนวนข้อมูลทั้งหมด
• yᵢ คือ ค่าจริงของข้อมูลตัวที่ i
• ŷᵢ คือ ค่าที่โมเดลทำนายของข้อมูลตัวที่ i

1. R-squared (R²) หรือ สัมประสิทธิ์การตัดสินใจ วัดว่าโมเดลสามารถอธิบายความแปรปรวนของข้อมูลได้ดีแค่ไหน มีค่าอยู่ระหว่าง 0 ถึง 1 ค่าที่ใกล้ 1 แสดงว่าโมเดลอธิบายข้อมูลได้ดี

$$R^2 = 1 - \frac{\text{SS}_{\text{res}}}{\text{SS}_{\text{tot}}}$$

โดยที่

• SSres คือ Sum of Squares of Residuals หรือ ผลรวมกำลังสองของความแตกต่างระหว่างค่าจริงและค่าที่ทำนาย $\sum (y_i - \hat{y}_i)^2$
• SStot คือ Total Sum of Squares หรือ ผลรวมกำลังสองของความแตกต่างระหว่างค่าจริงและค่าเฉลี่ยของค่าจริง $\sum (y_i - \hat{y}_i)^2$
• ȳ คือ ค่าเฉลี่ยของค่าจริงทั้งหมด

ความแตกต่างและการใช้งานแต่ละสมการ

• MAE เหมาะสำหรับกรณีที่ข้อมูลมีค่าผิดปกติ (outliers) เพราะไม่ได้รับผลกระทบจากค่าผิดปกติมากเท่า MSE
• MSE ให้ความสำคัญกับความผิดพลาดขนาดใหญ่มากกว่าความผิดพลาดขนาดเล็ก เพราะมีการยกกำลังสอง
• RMSE มีหน่วยเดียวกับตัวแปรเป้าหมาย ทำให้ง่ายต่อการตีความ และมักถูกใช้มากกว่า MSE
• R² บอกถึงความสามารถของโมเดลในการอธิบายความแปรปรวนของข้อมูล แต่ไม่สามารถบอกถึงขนาดของความผิดพลาดได้

ตัวอย่างการตีความ สมมติว่าเรามีโมเดลทำนายราคาสินค้า

• ถ้า RMSE = 100 บาท หมายความว่าโดยเฉลี่ยแล้ว โมเดลทำนายราคาผิดพลาดไป 100 บาท
• ถ้า R² = 0.8 หมายความว่าโมเดลสามารถอธิบายความแปรปรวนของราคาสินค้าได้ 80% ส่วนอีก 20% อธิบายไม่ได้ด้วยโมเดลนี้

ดังนั้น การเลือกใช้วิธีการวัดคุณภาพขึ้นอยู่กับลักษณะของข้อมูลและวัตถุประสงค์ของงาน ควรพิจารณา metric หลายๆ อย่างประกอบกัน เพื่อให้ได้ภาพรวมที่ครอบคลุมเกี่ยวกับประสิทธิภาพของโมเดล และเลือกใช้ metric ที่เหมาะสมกับบริบทของปัญหา

นอกจากนี้ ยังมี metric อื่นๆ ที่ใช้ในการวัดคุณภาพของ Regression Model เช่น Adjusted R-squared ซึ่งปรับ R-squared เพื่อพิจารณาจำนวนตัวแปรในโมเดล และควรพิจารณาเรื่อง Overfitting และ Underfitting ของโมเดลประกอบด้วย ซึ่งเป็นส่วนสำคัญในการประเมินประสิทธิภาพของโมเดลให้ดียิ่งขึ้นได้เช่นกัน

ข้อจำกัดของ Regression Analysis

Regression Analysis เป็นเครื่องมือทางสถิติที่มีประโยชน์อย่างมากสำหรับการศึกษาความสัมพันธ์ระหว่างตัวแปร แต่ก็มีข้อจำกัดบางประการที่ต้องพิจารณา เพื่อให้การวิเคราะห์และการตีความผลลัพธ์เป็นไปอย่างถูกต้อง ข้อจำกัดที่สำคัญมีดังนี้

1. การพึ่งพาสมมติฐานของโมเดล (Model Assumptions)

การวิเคราะห์การถดถอยตั้งอยู่บนสมมติฐานหลายประการ หากสมมติฐานเหล่านี้ไม่เป็นจริง ผลลัพธ์ที่ได้อาจไม่ถูกต้องหรือไม่น่าเชื่อถือ สมมติฐานที่สำคัญเช่น

• ความเป็นเส้นตรง (Linearity): สมมติว่ามีความสัมพันธ์เชิงเส้นระหว่างตัวแปรอิสระและตัวแปรตาม หากความสัมพันธ์เป็นแบบไม่เชิงเส้น (เช่น โค้ง) การใช้การถดถอยเชิงเส้นอาจให้ผลลัพธ์ที่ไม่ถูกต้อง การตรวจสอบความเป็นเส้นตรงสามารถทำได้โดยการ plot กราฟ Scatter plot ระหว่างตัวแปรอิสระและตัวแปรตาม หรือ plot กราฟ Residual plot
• ความเป็นอิสระของความคลาดเคลื่อน (Independence of Errors): สมมติว่าความคลาดเคลื่อน (residuals) ของแต่ละค่าสังเกตเป็นอิสระต่อกัน นั่นคือ ความคลาดเคลื่อนของข้อมูลหนึ่งไม่ควรมีผลต่อความคลาดเคลื่อนของข้อมูลอื่น โดยเฉพาะอย่างยิ่งในข้อมูลอนุกรมเวลา (Time series data) ที่มักเกิดปัญหา Autocorrelation หรือความสัมพันธ์ของความคลาดเคลื่อนในแต่ละช่วงเวลา การตรวจสอบสามารถทำได้โดยใช้ Durbin-Watson test หรือการ plot กราฟ Autocorrelation function (ACF) และ Partial Autocorrelation function (PACF)
• ความแปรปรวนคงที่ของความคลาดเคลื่อน (Homoscedasticity): สมมติว่าความแปรปรวนของความคลาดเคลื่อนมีค่าคงที่สำหรับทุกระดับของตัวแปรอิสระ หากความแปรปรวนไม่คงที่ (Heteroscedasticity) การประมาณค่าสัมประสิทธิ์อาจไม่มีประสิทธิภาพ การตรวจสอบสามารถทำได้โดยการ plot กราฟ Residual plot โดยดูการกระจายตัวของจุด ถ้าความแปรปรวนไม่คงที่ จุดจะกระจายตัวเป็นรูปกรวยหรือรูปร่างอื่นๆ ที่ไม่สม่ำเสมอ
• การแจกแจงแบบปกติของความคลาดเคลื่อน (Normality of Errors): สมมติว่าความคลาดเคลื่อนมีการแจกแจงแบบปกติ สมมติฐานนี้มีความสำคัญโดยเฉพาะอย่างยิ่งเมื่อใช้การทดสอบสมมติฐานและการสร้างช่วงความเชื่อมั่น การตรวจสอบสามารถทำได้โดยใช้ histogram, Q-Q plot หรือการทดสอบ Shapiro-Wilk test
• ไม่มีความสัมพันธ์ระหว่างตัวแปรอิสระกับความคลาดเคลื่อน (No Correlation between Independent Variables and Errors): สมมติว่าไม่มีความสัมพันธ์ระหว่างตัวแปรอิสระกับความคลาดเคลื่อน หากมีความสัมพันธ์ อาจเกิดปัญหา Endogeneity ทำให้การประมาณค่า Bias และ Inconsistent

หากสมมติฐานเหล่านี้ไม่เป็นจริง อาจต้องใช้วิธีการแก้ไข เช่น การแปลงข้อมูล (transformation), การใช้วิธีการถดถอยแบบอื่น (เช่น Non-linear regression), หรือการใช้ robust standard errors

2. ปัญหา Multicollinearity

Multicollinearity เกิดขึ้นเมื่อมีตัวแปรอิสระสองตัวขึ้นไปในโมเดลที่มีความสัมพันธ์เชิงเส้นสูง ปัญหานี้ทำให้เกิด

• การประมาณค่าสัมประสิทธิ์ที่ไม่แม่นยำ: ค่าสัมประสิทธิ์อาจมีค่ามากเกินไป มีเครื่องหมายตรงกันข้ามกับที่คาดหวัง หรือมีความไม่แน่นอนสูง (ค่า Standard error สูง)
• การตีความผลลัพธ์ที่ยากลำบาก: ยากที่จะแยกแยะผลกระทบของตัวแปรอิสระแต่ละตัวต่อตัวแปรตาม

การตรวจสอบ Multicollinearity

• Correlation matrix: ตรวจสอบค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างตัวแปรอิสระ หากค่าสัมประสิทธิ์มีค่าสูง (เช่น มากกว่า 0.7 หรือ 0.8 ในบางกรณี) แสดงว่ามีความเสี่ยงของ Multicollinearity
• Variance Inflation Factor (VIF): คำนวณ VIF สำหรับตัวแปรอิสระแต่ละตัว VIF บอกว่าความแปรปรวนของสัมประสิทธิ์เพิ่มขึ้นเท่าใดเนื่องจาก Multicollinearity โดยทั่วไป หาก VIF มีค่ามากกว่า 5 หรือ 10 แสดงว่ามีความเสี่ยงของ Multicollinearity
• Eigenvalues and Condition Index: วิเคราะห์ Eigenvalues ของ correlation matrix และคำนวณ Condition Index ค่า Condition Index ที่สูง (เช่น มากกว่า 30) บ่งบอกถึง Multicollinearity

การแก้ไข Multicollinearity:

• การลบตัวแปร: หากตัวแปรสองตัวมีความสัมพันธ์กันสูง อาจเลือกที่จะลบตัวแปรใดตัวแปรหนึ่งออก
• การรวมตัวแปร: สร้างตัวแปรใหม่โดยรวมตัวแปรที่มีความสัมพันธ์กัน
• การเพิ่มข้อมูล: การเพิ่มจำนวนข้อมูลอาจช่วยลดผลกระทบของ Multicollinearity
• Principal Component Analysis (PCA): ใช้ PCA เพื่อสร้างตัวแปรใหม่ที่เป็นอิสระต่อกัน

ดังนั้น สรุปคือ Regression Analysis เป็นเครื่องมือที่มีประสิทธิภาพ แต่ต้องระมัดระวังข้อจำกัดและสมมติฐานต่างๆ การตรวจสอบและแก้ไขปัญหาต่างๆ เช่น Multicollinearity และการละเมิดสมมติฐาน จะช่วยให้ได้ผลลัพธ์ที่น่าเชื่อถือและถูกต้องมากขึ้นได้นั่นเอง