Hypothesis Testing

Hypothesis Testing คืออะไร

Hypothesis Testing คือกระบวนการทางสถิติที่ใช้ในการตัดสินใจว่าสมมติฐานที่ตั้งไว้เกี่ยวกับประชากรนั้นมีความเป็นไปได้มากน้อยเพียงใด โดยอาศัยข้อมูลจากตัวอย่างที่สุ่มเลือกมา

ในการศึกษาหรือวิจัย เรามักจะมีความเชื่อหรือการคาดเดาเกี่ยวกับปรากฏการณ์หรือประชากรที่เราสนใจ เช่น "ยาใหม่มีประสิทธิภาพในการรักษาสูงกว่ายาเก่า" หรือ "ค่าเฉลี่ยของรายได้ของประชากรในจังหวัด A สูงกว่าจังหวัด B" การคาดเดาเหล่านี้เรียกว่า "สมมติฐาน”

การทดสอบสมมติฐานจึงเป็นกระบวนการในการตรวจสอบว่าข้อมูลที่เราเก็บรวบรวมมานั้นสนับสนุนหรือคัดค้านสมมติฐานที่เราตั้งไว้

ขั้นตอนของการทดสอบสมมติฐานโดยทั่วไปประกอบด้วย

ตั้งสมมติฐาน: กำหนดสมมติฐานหลัก (Null Hypothesis หรือ H0) ซึ่งมักจะเป็นสมมติฐานที่บ่งบอกว่า "ไม่มีความแตกต่าง" หรือ "ไม่มีความสัมพันธ์" และสมมติฐานทางเลือก (Alternative Hypothesis หรือ H1) ซึ่งเป็นสิ่งที่ผู้วิจัยต้องการพิสูจน์ เช่น
- H0: ยาใหม่และยาเก่ามีประสิทธิภาพไม่แตกต่างกัน
- H1: ยาใหม่มีประสิทธิภาพสูงกว่ายาเก่า
กำหนดระดับนัยสำคัญ (Significance Level หรือ α): กำหนดค่าความน่าจะเป็นที่จะปฏิเสธสมมติฐานหลักในขณะที่สมมติฐานหลักเป็นจริง (มักกำหนดไว้ที่ 0.05 หรือ 5%)
เลือกสถิติที่ใช้ในการทดสอบ: เลือกวิธีการทางสถิติที่เหมาะสมกับลักษณะของข้อมูลและสมมติฐาน เช่น t-test, chi-square test, ANOVA
คำนวณค่าสถิติและค่า p-value: คำนวณค่าสถิติจากข้อมูลตัวอย่าง และคำนวณค่า p-value ซึ่งเป็นความน่าจะเป็นที่จะได้ผลลัพธ์ที่สังเกตเห็นหรือมากกว่า หากสมมติฐานหลักเป็นจริง
ตัดสินใจ: เปรียบเทียบค่า p-value กับระดับนัยสำคัญ ถ้าค่า p-value น้อยกว่าระดับนัยสำคัญ จะปฏิเสธสมมติฐานหลัก และยอมรับสมมติฐานทางเลือก

ความสำคัญของการทดสอบสมมติฐานในการวิเคราะห์ข้อมูล

ช่วยในการตัดสินใจอย่างมีหลักเกณฑ์: การทดสอบสมมติฐานช่วยให้เราตัดสินใจได้อย่างเป็นระบบและมีหลักเกณฑ์ โดยอาศัยข้อมูลเชิงประจักษ์ แทนที่จะใช้เพียงความรู้สึกหรือการคาดเดา
ช่วยในการสรุปผลและอ้างอิง: ช่วยให้เราสรุปผลการวิเคราะห์ข้อมูลและอ้างอิงไปยังประชากรได้อย่างมั่นใจมากขึ้น
ช่วยในการวิจัยและพัฒนา: มีบทบาทสำคัญในการวิจัยและพัฒนาในหลากหลายสาขา เช่น การแพทย์ การตลาด วิทยาศาสตร์ และวิศวกรรม
ช่วยในการตรวจสอบความถูกต้องของทฤษฎี: ช่วยในการตรวจสอบว่าทฤษฎีหรือสมมติฐานที่ตั้งไว้นั้นสอดคล้องกับข้อมูลจริงหรือไม่

เราจะเริ่มทำความเข้าใจไปทีละขั้นตอนและทีละองค์ประกอบกันนะครับ

สมมุติฐานคืออะไร

เพื่อให้เกิดความเข้าใจที่มากขึ้น เราต้องทำความรู้จักอย่างลึกซึ้งเรื่องการตั้งสมมุติฐานหรือ Hypothesis กันก่อน

สมมุติฐานคือการคาดเดาหรือคำอธิบายเบื้องต้นเกี่ยวกับปรากฏการณ์หรือความสัมพันธ์ระหว่างสิ่งต่างๆ ที่ยังไม่ได้พิสูจน์หรือยืนยันอย่างแน่ชัด เป็นการคาดการณ์ที่ตั้งขึ้นเพื่อใช้เป็นแนวทางในการศึกษาหรือทดสอบต่อไป โดยทั่วไป สมมุติฐานที่ดีควรมีลักษณะดังนี้

สามารถทดสอบได้ (Testable): สามารถตรวจสอบได้โดยใช้ข้อมูลเชิงประจักษ์หรือการทดลอง
ชัดเจนและเฉพาะเจาะจง (Clear and Specific): ระบุความสัมพันธ์ระหว่างตัวแปรอย่างชัดเจน
มีเหตุผลและอิงกับทฤษฎีหรือความรู้ที่มีอยู่ (Reasonable and Based on Existing Knowledge): ไม่ใช่การคาดเดาแบบไร้เหตุผล

ตัวอย่าง "การดื่มกาแฟมีผลต่อการนอนหลับ" เป็นสมมุติฐานที่กว้างๆ เราสามารถทำให้เฉพาะเจาะจงขึ้นได้ เช่น "การดื่มกาแฟ 1 แก้วก่อนนอนจะทำให้นอนหลับยากขึ้น”

โดยในการทดสอบสมมุติฐานทางสถิติ เราจะแบ่งสมมุติฐานออกเป็นสองประเภทหลักๆ คือ

Null Hypothesis (H₀) หรือ สมมุติฐานว่าง เป็นสมมุติฐานที่ระบุว่า "ไม่มีความแตกต่าง" "ไม่มีความสัมพันธ์" หรือ "ไม่มีผลกระทบ" ระหว่างสิ่งที่สนใจ เป็นสิ่งที่ผู้วิจัยต้องการจะปฏิเสธหรือล้มล้าง

มักใช้เครื่องหมายเท่ากับ (=), น้อยกว่าหรือเท่ากับ (≤), หรือมากกว่าหรือเท่ากับ (≥)
ตัวอย่างเช่น
- H₀: การดื่มกาแฟไม่มีผลต่อการนอนหลับ (ค่าเฉลี่ยของระยะเวลาการนอนหลับของผู้ที่ดื่มกาแฟและผู้ที่ไม่ได้ดื่มกาแฟไม่แตกต่างกัน)
- H₀: ยาใหม่มีประสิทธิภาพไม่แตกต่างจากยาเก่า
- H₀: เพศชายและเพศหญิงมีรายได้เฉลี่ยเท่ากัน

Alternative Hypothesis (H₁) หรือ สมมุติฐานทางเลือก (บางครั้งเรียกว่า Research Hypothesis หรือ สมมุติฐานการวิจัย) เป็นสมมุติฐานที่ระบุว่า "มีความแตกต่าง" "มีความสัมพันธ์" หรือ "มีผลกระทบ" เป็นสิ่งที่ผู้วิจัยต้องการจะพิสูจน์หรือสนับสนุน

มักใช้เครื่องหมายไม่เท่ากับ (≠), มากกว่า (>), หรือน้อยกว่า (<)
ตัวอย่างเช่น
- H₁: การดื่มกาแฟมีผลต่อการนอนหลับ (ค่าเฉลี่ยของระยะเวลาการนอนหลับของผู้ที่ดื่มกาแฟและผู้ที่ไม่ได้ดื่มกาแฟแตกต่างกัน)
- H₁: ยาใหม่มีประสิทธิภาพสูงกว่ายาเก่า
- H₁: เพศชายมีรายได้เฉลี่ยสูงกว่าเพศหญิง

โดย H₀ และ H₁ เป็นสิ่งที่ตรงกันข้ามกัน ไม่สามารถเป็นจริงทั้งคู่ได้ หาก H₀ เป็นจริง H₁ จะเป็นเท็จ และในทางกลับกัน หาก H₁ เป็นจริง H₀ จะเป็นเท็จ

คำถามก็คือ “ทำไมต้องมีทั้ง H₀ และ H₁?”

ในการทดสอบสมมุติฐาน เราจะพยายามหาหลักฐานเพื่อปฏิเสธ H₀ หากเราสามารถปฏิเสธ H₀ ได้อย่างมีนัยสำคัญทางสถิติ แสดงว่ามีหลักฐานสนับสนุน H₁ อยู่นั่นเอง

ตัวอย่างการตั้งสมมุติฐานเพิ่มเติม

สมมติว่าเราต้องการศึกษาว่าการใช้ application ช่วยเรียนภาษาอังกฤษมีผลต่อคะแนนสอบ toeic หรือไม่

H₀: การใช้ application ช่วยเรียนภาษาอังกฤษไม่มีผลต่อคะแนนสอบ toeic (ค่าเฉลี่ยคะแนนสอบ toeic ของผู้ที่ใช้แอปฯ และผู้ที่ไม่ได้ใช้แอปฯ ไม่แตกต่างกัน)
H₁: การใช้ application ช่วยเรียนภาษาอังกฤษมีผลต่อคะแนนสอบ toeic (ค่าเฉลี่ยคะแนนสอบ toeic ของผู้ที่ใช้แอปฯ และผู้ที่ไม่ได้ใช้แอปฯ แตกต่างกัน) หรืออาจจะตั้ง H₁ แบบเจาะจงขึ้น เช่น H₁: การใช้ application ช่วยเรียนภาษาอังกฤษทำให้คะแนนสอบ toeic สูงขึ้น (ค่าเฉลี่ยคะแนนสอบ toeic ของผู้ที่ใช้แอปฯ สูงกว่าผู้ที่ไม่ได้ใช้แอปฯ)

ทีนี้คำถามต่อมา “แล้วเราจะรู้ได้อย่างไรว่า เราเลือก Null Hypothesis ถูกต้องแล้ว ?”

การจะรู้ว่าเราเลือก Null Hypothesis (H₀) ได้ถูกต้องหรือไม่นั้น ไม่ได้หมายถึงการ "พิสูจน์" ว่า H₀ เป็นจริง เพราะในการทดสอบสมมติฐาน เราจะพยายามหาหลักฐานเพื่อ "ปฏิเสธ" H₀ มากกว่า การเลือก H₀ ที่ถูกต้องจึงหมายถึงการตั้ง H₀ ที่เหมาะสมกับคำถามวิจัยและกระบวนการทดสอบ ซึ่งมีหลักการดังนี้

H₀ ต้องเป็นสิ่งที่สามารถถูกปฏิเสธได้

แก่นของการทดสอบสมมติฐานคือการหาหลักฐานเพื่อปฏิเสธ H₀ ดังนั้น H₀ ต้องอยู่ในรูปแบบที่สามารถถูกปฏิเสธได้โดยข้อมูลเชิงประจักษ์
โดยทั่วไป H₀ จะอยู่ในรูปของ "ไม่มีความแตกต่าง" "ไม่มีความสัมพันธ์" หรือ "ไม่มีผลกระทบ" ซึ่งเป็นสิ่งที่ง่ายต่อการตรวจสอบว่ามีหลักฐานขัดแย้งหรือไม่

ตัวอย่างเช่น

ถ้าเราต้องการศึกษาว่ายาใหม่มีประสิทธิภาพดีกว่ายาเก่าหรือไม่ เราจะตั้ง H₀ ว่า "ยาใหม่และยาเก่ามีประสิทธิภาพไม่แตกต่างกัน" (H₀: μ₁ = μ₂) ซึ่งสามารถถูกปฏิเสธได้ถ้าพบว่ายาใหม่มีประสิทธิภาพสูงกว่าอย่างมีนัยสำคัญ
เราจะไม่ตั้ง H₀ ว่า "ยาใหม่มีประสิทธิภาพดีกว่ายาเก่า" เพราะถ้าผลการทดสอบไม่พบความแตกต่าง ก็ไม่สามารถ "ปฏิเสธ" H₀ ได้

H₀ สะท้อนถึงสถานะที่เป็นอยู่หรือความเชื่อเดิม

H₀ มักจะแสดงถึงสถานะที่เป็นอยู่ (Status quo) หรือความเชื่อเดิมที่ยังไม่มีหลักฐานมาลบล้าง
การตั้ง H₀ ในลักษณะนี้จะช่วยให้เราทำการทดสอบเพื่อหาหลักฐานที่จะเปลี่ยนแปลงความเชื่อเดิมนั้น

ตัวอย่างเช่น

ก่อนที่จะมียาใหม่ เราอาจจะเชื่อว่ายาเก่าเป็นวิธีรักษาที่ดีที่สุด ดังนั้นเราจะตั้ง H₀ ว่า "ยาใหม่และยาเก่ามีประสิทธิภาพไม่แตกต่างกัน" เพื่อทดสอบว่ายาใหม่ดีกว่าจริงหรือไม่
ในการตลาด เราอาจจะเชื่อว่าโฆษณาแบบเดิมมีประสิทธิภาพอยู่แล้ว ดังนั้นเราจะตั้ง H₀ ว่า "การใช้โฆษณาแบบใหม่ไม่มีผลต่อยอดขาย" เพื่อทดสอบว่าโฆษณาแบบใหม่ช่วยเพิ่มยอดขายได้จริงหรือไม่

H₀ สอดคล้องกับคำถามวิจัย

H₀ ต้องสอดคล้องกับคำถามวิจัยที่เราต้องการศึกษา
คำถามวิจัยจะกำหนดทิศทางของการตั้งสมมติฐาน และ H₀ ควรจะเป็นสิ่งที่ตรงกันข้ามกับสิ่งที่เราต้องการพิสูจน์

ตัวอย่างเช่น

คำถามวิจัย: การออกกำลังกายสม่ำเสมอช่วยลดน้ำหนักได้จริงหรือไม่?
H₀: การออกกำลังกายสม่ำเสมอไม่มีผลต่อน้ำหนัก (H₀: μ₁ = μ₂)
H₁: การออกกำลังกายสม่ำเสมอช่วยลดน้ำหนัก (H₁: μ₁ < μ₂)

พิจารณาประเภทของการทดสอบ

การทดสอบสมมติฐานมีสองประเภทหลักๆ คือ การทดสอบแบบทางเดียว (One-tailed test) และการทดสอบแบบสองทาง (Two-tailed test) (เดี๋ยวเราจะมีอธิบายอีกที)
การเลือกประเภทของการทดสอบจะส่งผลต่อการตั้ง H₀ และ H₁
- การทดสอบแบบสองทาง: ใช้เมื่อเราต้องการทดสอบว่ามีความแตกต่างกันหรือไม่ โดยไม่สนใจว่าจะเป็นไปในทิศทางใด (มากกว่าหรือน้อยกว่า) H₀ จะอยู่ในรูปของ "เท่ากับ" (เช่น H₀: μ₁ = μ₂)
- การทดสอบแบบทางเดียว: ใช้เมื่อเราต้องการทดสอบว่ามีทิศทางที่เฉพาะเจาะจง เช่น มากกว่า หรือ น้อยกว่า H₀ จะอยู่ในรูปของ "น้อยกว่าหรือเท่ากับ" (≤) หรือ "มากกว่าหรือเท่ากับ" (≥)

ดังนั้นการเลือก H₀ ที่ถูกต้องไม่ได้หมายถึงการพิสูจน์ว่า H₀ เป็นจริง แต่เป็นการตั้ง H₀ ที่เหมาะสมกับการทดสอบ โดยมีหลักการคือ H₀ ต้องสามารถถูกปฏิเสธได้ สะท้อนถึงสถานะที่เป็นอยู่ สอดคล้องกับคำถามวิจัย และพิจารณาประเภทของการทดสอบ

สิ่งสำคัญคือต้องเข้าใจว่าการทดสอบสมมติฐานเป็นการหาหลักฐานเพื่อ ปฏิเสธ H₀ ถ้าเราไม่สามารถปฏิเสธ H₀ ได้ หมายความว่าไม่มีหลักฐานเพียงพอที่จะสรุปว่า H₀ เป็นเท็จ “ไม่ได้หมายความว่า H₀ เป็นจริง” นั่นเอง

การเลือก Test Statistic

Step ต่อมาหลังจากเลือก ข้อสันนิษฐานแล้ว เราจะทำการเลือกสถิติมาทดสอบกัน

การเลือกว่าจะใช้สถิติใดในการทดสอบสมมติฐานกับข้อมูลตัวอย่าง ขึ้นอยู่กับปัจจัยหลายประการ การเข้าใจปัจจัยเหล่านี้จะช่วยให้คุณเลือกวิธีการทางสถิติที่เหมาะสมและได้ผลลัพธ์ที่ถูกต้อง

ปัจจัยที่ใช้ในการพิจารณาเลือกสถิติ

วัตถุประสงค์ของการวิจัย (Research Objective): สิ่งที่คุณต้องการจะศึกษาหรือพิสูจน์ มีอิทธิพลอย่างมากต่อการเลือกสถิติ
- เปรียบเทียบค่าเฉลี่ย: หากต้องการเปรียบเทียบค่าเฉลี่ยของกลุ่มตัวอย่างกับค่าคงที่ หรือเปรียบเทียบค่าเฉลี่ยระหว่างสองกลุ่ม หรือมากกว่าสองกลุ่ม มักใช้ t-test หรือ ANOVA
- หาความสัมพันธ์: หากต้องการหาความสัมพันธ์ระหว่างตัวแปรสองตัวแปร มักใช้ Correlation หรือ Regression analysis
- ทดสอบความแตกต่างของสัดส่วน: หากต้องการทดสอบความแตกต่างของสัดส่วนหรือความถี่ มักใช้ Chi-square test
ประเภทของข้อมูล (Types of Data): ระดับการวัดของข้อมูลมีผลต่อการเลือกสถิติ
- Nominal (นามบัญญัติ): ข้อมูลที่ใช้แบ่งกลุ่มเท่านั้น เช่น เพศ ศาสนา กรุ๊ปเลือด ไม่สามารถนำมาคำนวณทางคณิตศาสตร์ได้ มักใช้ Chi-square test หรือการวิเคราะห์ความถี่
- Ordinal (เรียงอันดับ): ข้อมูลที่สามารถเรียงลำดับได้ แต่ช่วงห่างระหว่างอันดับไม่เท่ากัน เช่น ระดับการศึกษา ระดับความพึงพอใจ มักใช้สถิติ Non-parametric เช่น Mann-Whitney U test หรือ Wilcoxon signed-rank test
- Interval (ช่วง): ข้อมูลที่มีช่วงห่างระหว่างค่าเท่ากัน แต่ไม่มีศูนย์แท้ เช่น อุณหภูมิเซลเซียส มักใช้ t-test หรือ ANOVA
- Ratio (อัตราส่วน): ข้อมูลที่มีช่วงห่างระหว่างค่าเท่ากัน และมีศูนย์แท้ เช่น ความสูง น้ำหนัก รายได้ มักใช้ t-test, ANOVA หรือ Regression analysis
จำนวนกลุ่มตัวอย่าง (Number of Samples):
- หนึ่งกลุ่ม: one-sample t-test หรือ z-test
- สองกลุ่ม: independent samples t-test (กลุ่มตัวอย่างเป็นอิสระต่อกัน) หรือ paired samples t-test (กลุ่มตัวอย่างมีความสัมพันธ์กัน เช่น วัดก่อนและหลัง)
- มากกว่าสองกลุ่ม: ANOVA (Analysis of Variance)
ความเป็นอิสระของกลุ่มตัวอย่าง (Independence of Samples):
- อิสระกัน: เช่น เปรียบเทียบผลการเรียนของนักเรียนสองห้องที่ต่างกัน
- สัมพันธ์กัน: เช่น เปรียบเทียบความดันโลหิตของคนไข้ก่อนและหลังการใช้ยา
การกระจายของข้อมูล (Data Distribution):
- มีการกระจายปกติ (Normal Distribution): มักใช้สถิติแบบ Parametric เช่น t-test, ANOVA
- ไม่มีการกระจายปกติ (Non-normal Distribution): มักใช้สถิติแบบ Non-parametric เช่น Mann-Whitney U test, Wilcoxon signed-rank test, Kruskal-Wallis test

ตารางสรุปการเลือกใช้สถิติเบื้องต้น

วัตถุประสงค์	ประเภทข้อมูล	จำนวนกลุ่ม	ความเป็นอิสระ	การกระจาย	สถิติที่ใช้
เปรียบเทียบค่าเฉลี่ยกับค่าคงที่	Interval/Ratio	1	-	ปกติ	one-sample t-test หรือ z-test
เปรียบเทียบค่าเฉลี่ยสองกลุ่ม	Interval/Ratio	2	อิสระ	ปกติ	independent samples t-test
เปรียบเทียบค่าเฉลี่ยสองกลุ่ม	Interval/Ratio	2	สัมพันธ์กัน	ปกติ	paired samples t-test
เปรียบเทียบค่าเฉลี่ยมากกว่าสองกลุ่ม	Interval/Ratio	>2	อิสระ	ปกติ	ANOVA
หาความสัมพันธ์ระหว่างสองตัวแปร	Interval/Ratio	-	-	-	Correlation (Pearson) หรือ Regression analysis
หาความสัมพันธ์ระหว่างสองตัวแปร	Ordinal	-	-	-	Correlation (Spearman)
ทดสอบความแตกต่างของสัดส่วน/ความถี่	Nominal/Ordinal	-	-	-	Chi-square test
เปรียบเทียบค่าเฉลี่ยสองกลุ่ม	Ordinal	2	อิสระ	ไม่ปกติ	Mann-Whitney U test
เปรียบเทียบค่าเฉลี่ยสองกลุ่ม	Ordinal	2	สัมพันธ์กัน	ไม่ปกติ	Wilcoxon signed-rank test
เปรียบเทียบค่าเฉลี่ยมากกว่าสองกลุ่ม	Ordinal	>2	อิสระ	ไม่ปกติ	Kruskal-Wallis test

ตัวอย่าง

ต้องการเปรียบเทียบความพึงพอใจในการใช้ application 2 ตัว โดยให้ผู้ใช้งานให้คะแนนความพึงพอใจเป็นระดับ (1-5) ข้อมูลเป็นแบบ Ordinal และกลุ่มตัวอย่างเป็นอิสระกัน ควรใช้ Mann-Whitney U test
ต้องการศึกษาว่ารายได้มีผลต่อการบริโภคหรือไม่ ข้อมูลเป็นแบบ Ratio ควรใช้ Regression analysis
ต้องการทดสอบว่าสัดส่วนของผู้ชายและผู้หญิงที่ชอบดูฟุตบอลแตกต่างกันหรือไม่ ข้อมูลเป็นแบบ Nominal ควรใช้ Chi-square test

เพิ่มเติมสถิติในแต่ละประเภทที่มักจะใช้บ่อย

Z-test
- ใช้เมื่อทราบค่าเบี่ยงเบนมาตรฐานของประชากร (σ) หรือขนาดตัวอย่างมีขนาดใหญ่มาก (โดยทั่วไป n > 30) และข้อมูลมีการกระจายแบบปกติ
- ใช้สำหรับการทดสอบค่าเฉลี่ยของประชากรกลุ่มเดียว หรือเปรียบเทียบค่าเฉลี่ยของสองกลุ่มที่เป็นอิสระกัน
t-test
- ใช้เมื่อไม่ทราบค่าเบี่ยงเบนมาตรฐานของประชากร และขนาดตัวอย่างมีขนาดเล็ก (โดยทั่วไป n < 30) หรือขนาดตัวอย่างมีขนาดใหญ่แต่ไม่ทราบค่าเบี่ยงเบนมาตรฐานของประชากร
- มีหลายประเภท
  - One-sample t-test: ทดสอบค่าเฉลี่ยของประชากรกลุ่มเดียว
  - Independent samples t-test (Two-sample t-test): เปรียบเทียบค่าเฉลี่ยของสองกลุ่มที่เป็นอิสระกัน
  - Paired samples t-test (Dependent samples t-test): เปรียบเทียบค่าเฉลี่ยของสองกลุ่มที่สัมพันธ์กัน เช่น การวัดก่อนและหลังในกลุ่มเดียวกัน
Chi-square test (χ² test)
- ใช้กับข้อมูลเชิงคุณภาพ (nominal หรือ ordinal)
- ใช้สำหรับการทดสอบความสัมพันธ์ระหว่างตัวแปรสองตัว (test of independence) หรือทดสอบความสอดคล้องกับสัดส่วนที่คาดหวัง (goodness-of-fit test)
ANOVA (Analysis of Variance)
- ใช้สำหรับการเปรียบเทียบค่าเฉลี่ยของมากกว่าสองกลุ่ม
- มีหลายประเภท:
  - One-way ANOVA: เปรียบเทียบค่าเฉลี่ยของกลุ่มที่จำแนกตามตัวแปรเดียว
  - Two-way ANOVA: เปรียบเทียบค่าเฉลี่ยของกลุ่มที่จำแนกตามสองตัวแปร
Correlation (สหสัมพันธ์)
- ใช้วัดความสัมพันธ์เชิงเส้นระหว่างตัวแปรสองตัว
- Pearson correlation: ใช้กับข้อมูล interval หรือ ratio ที่มีการกระจายแบบปกติ
- Spearman correlation: ใช้กับข้อมูล ordinal หรือข้อมูลที่ไม่เป็นไปตามข้อตกลงของการกระจายแบบปกติ

ก่อนที่เราจะเริ่ม step ของการทดสอบสถิติ เราจะต้องรู้จักอีก 2 ค่าที่เราจะต้องนำมาประกอบการทดสอบ นั่นคือ ระดับนัยสำคัญ และ P value กันก่อน

ระดับนัยสำคัญ และ P value

ระดับนัยสำคัญ (Significance level หรือ alpha, α) และค่า P (P-value) เป็นสองแนวคิดสำคัญในการทดสอบสมมติฐานทางสถิติ มีความสัมพันธ์กันอย่างใกล้ชิด และใช้ในการตัดสินใจว่าจะปฏิเสธสมมติฐานหลัก (Null hypothesis) หรือไม่

ระดับนัยสำคัญ (Significance level, α)

เป็นค่าความน่าจะเป็นที่เรายอมรับได้ในการที่จะปฏิเสธสมมติฐานหลัก ทั้งๆ ที่สมมติฐานหลักนั้นเป็นจริง หรือเรียกว่า "ความผิดพลาดประเภทที่ 1" (Type I error หรือ False positive)
โดยทั่วไปนิยมกำหนดค่า α ที่ 0.05 (5%), 0.01 (1%) หรือ 0.10 (10%)
เช่น ถ้ากำหนด α = 0.05 หมายความว่า เรายอมรับความเสี่ยงที่จะตัดสินใจผิดพลาด (ปฏิเสธสมมติฐานหลักเมื่อเป็นจริง) ได้ 5%

ค่า P (P-value)

เป็นค่าความน่าจะเป็นที่จะได้ผลลัพธ์ที่สังเกตได้ หรือผลลัพธ์ที่รุนแรงกว่า (มีความแตกต่างจากสมมติฐานหลักมากกว่า) หากสมมติฐานหลักเป็นจริง
ค่า P บ่งบอกถึงความแข็งแกร่งของหลักฐานที่ขัดแย้งกับสมมติฐานหลัก
ค่า P มีค่าอยู่ระหว่าง 0 ถึง 1

ความสัมพันธ์ระหว่าง ระดับนัยสำคัญ (α) และ ค่า P (P-value)

เราจะนำค่า P มาเปรียบเทียบกับระดับนัยสำคัญ (α) เพื่อตัดสินใจว่าจะปฏิเสธสมมติฐานหลักหรือไม่ โดยมีหลักเกณฑ์ดังนี้

ถ้า P-value ≤ α: เราจะปฏิเสธสมมติฐานหลัก นั่นหมายความว่า ผลลัพธ์ที่ได้มีความสำคัญทางสถิติ (Statistically significant) และมีหลักฐานที่เพียงพอที่จะสนับสนุนสมมติฐานทางเลือก
ถ้า P-value > α: เราจะไม่ปฏิเสธสมมติฐานหลัก นั่นหมายความว่า ผลลัพธ์ที่ได้ไม่มีความสำคัญทางสถิติ และไม่มีหลักฐานที่เพียงพอที่จะสนับสนุนสมมติฐานทางเลือก

ตัวอย่าง

สมมติว่าเราทำการทดสอบเพื่อดูว่ายาใหม่มีผลต่อการลดความดันโลหิตหรือไม่ เราตั้งสมมติฐานดังนี้

สมมติฐานหลัก ( $H_0$ ): ยาใหม่ไม่มีผลต่อการลดความดันโลหิต
สมมติฐานทางเลือก ( $H_1$ ): ยาใหม่มีผลต่อการลดความดันโลหิต

เรากำหนดระดับนัยสำคัญ α = 0.05 และทำการทดสอบทางสถิติ ได้ค่า P-value = 0.03

เนื่องจาก P-value (0.03) น้อยกว่า α (0.05) เราจึงปฏิเสธสมมติฐานหลัก สรุปได้ว่า ยาใหม่มีผลต่อการลดความดันโลหิตอย่างมีนัยสำคัญทางสถิติ

ระดับนัยสำคัญ (α) คือเกณฑ์ที่เรากำหนดไว้ล่วงหน้าเพื่อตัดสินใจ ส่วนค่า P (P-value) คือผลลัพธ์ที่ได้จากการทดสอบ เมื่อนำมาเปรียบเทียบกันจะช่วยให้เราตัดสินใจได้อย่างเป็นระบบว่าจะยอมรับหรือปฏิเสธสมมติฐานหลักนั่นเอง

Note ข้อควรระวังในการใช้งาน

การมีนัยสำคัญทางสถิติไม่ได้หมายความถึงความสำคัญในทางปฏิบัติ (Practical significance) แม้ผลลัพธ์จะมีความแตกต่างอย่างมีนัยสำคัญทางสถิติ แต่ความแตกต่างนั้นอาจมีขนาดเล็กมากจนไม่มีความสำคัญในเชิงปฏิบัติ
ค่า P ไม่ได้บอกถึงความน่าจะเป็นที่สมมติฐานหลักจะเป็นจริง หรือความน่าจะเป็นที่สมมติฐานทางเลือกจะเป็นจริง

ทีนี้ ในการคำนวนมือหลายๆครั้ง ในการคำนวน p value จะค่อนข้างยุ่งยาก ดังนั้นจึงมีอีก concept นั่นคือ Critical value มาช่วยเรื่องนี้ (เนื่องจาก การคำนวณ p-value ด้วยมือหลายๆ ครั้งอาจเป็นเรื่องยุ่งยาก ดังนั้นแนวคิดของ Critical Value จึงถูกนำมาใช้เพื่อช่วยลดความซับซ้อนนี้ลงได้)

Critical Value คือ ค่าที่ใช้เป็นเส้นแบ่งเขตในการตัดสินใจว่าจะปฏิเสธหรือยอมรับสมมติฐานหลัก (Null Hypothesis) ในการทดสอบสมมติฐานทางสถิติ ค่านี้ได้มาจากตารางการแจกแจงความน่าจะเป็น เช่น ตารางการแจกแจง t, ตารางการแจกแจง Z หรือตารางการแจกแจง Chi-square ขึ้นอยู่กับการทดสอบที่เราใช้

โดยทั่วไป เราจะกำหนดระดับนัยสำคัญ (alpha หรือ α) ซึ่งมักจะอยู่ที่ 0.05 หรือ 5% ระดับนัยสำคัญนี้แสดงถึงความเสี่ยงที่เรายอมรับได้ที่จะปฏิเสธสมมติฐานหลัก ทั้งๆ ที่สมมติฐานหลักนั้นเป็นจริง (Type I error)

เมื่อเรารู้ค่า alpha และประเภทของการทดสอบ (เช่น การทดสอบทางเดียวหรือสองทาง) เราสามารถหา Critical Value จากตารางได้ ค่านี้จะแบ่งพื้นที่ใต้กราฟการแจกแจงออกเป็นสองส่วน คือ

บริเวณปฏิเสธ (Rejection Region): คือบริเวณที่อยู่เลย Critical Value ออกไป ถ้าค่าสถิติที่คำนวณได้จากการทดสอบตกอยู่ในบริเวณนี้ เราจะปฏิเสธสมมติฐานหลัก
บริเวณยอมรับ (Acceptance Region): คือบริเวณที่อยู่ระหว่าง Critical Value ถ้าค่าสถิติที่คำนวณได้ตกอยู่ในบริเวณนี้ เราจะไม่ปฏิเสธสมมติฐานหลัก

ความสัมพันธ์ระหว่าง p-value และ Critical Value

ทั้ง p-value และ Critical Value ใช้ในการตัดสินใจเกี่ยวกับการปฏิเสธสมมติฐานหลัก แต่ใช้วิธีการที่แตกต่างกัน

p-value: บอกถึงความน่าจะเป็นที่จะได้ผลลัพธ์ที่สังเกตได้ หรือผลลัพธ์ที่รุนแรงกว่า ถ้าสมมติฐานหลักเป็นจริง ถ้า p-value มีค่าน้อยกว่าระดับนัยสำคัญ (alpha) เราจะปฏิเสธสมมติฐานหลัก
Critical Value: เป็นค่าที่กำหนดขอบเขตของการปฏิเสธสมมติฐานหลัก โดยเปรียบเทียบกับค่าสถิติที่คำนวณได้จากการทดสอบ

ความสัมพันธ์ที่สำคัญคือ ถ้าค่าสถิติที่คำนวณได้มีค่า เลย Critical Value ไป นั่นหมายความว่า p-value จะมีค่าน้อยกว่า alpha เสมอ และในทางกลับกัน ถ้าค่าสถิติที่คำนวณได้อยู่ ภายใน Critical Value นั่นหมายความว่า p-value จะมีค่ามากกว่า alpha

One tailed Test และ Two tailed Test

Ref: https://www.geo.fu-berlin.de/en/v/soga-py/Basics-of-statistics/Hypothesis-Tests/Introduction-to-Hypothesis-Testing/Critical-Value-and-the-p-Value-Approach/index.html

นอกเหนือจากเรื่องสถิติที่ใช้ทดสอบแล้ว สมมุติฐานเองก็จะนำไปสู่การทดสอบที่ถูกต้องด้วยเช่นกัน โดยปกติจะมี 2 แบบคือ One tailed Test และ Two tailed Test

การทดสอบแบบ One-Tailed และ Two-Tailed เป็นกระบวนการทางสถิติที่ใช้ใน การทดสอบสมมติฐาน (Hypothesis Testing) เพื่อตรวจสอบว่ามีหลักฐานเพียงพอในการปฏิเสธสมมติฐานว่าง (H₀) หรือไม่ โดยความแตกต่างระหว่างสองวิธีนี้อยู่ที่การกำหนด สมมติฐานทางเลือก (H₁) และตำแหน่งของ Critical Region ซึ่งเป็นบริเวณที่ใช้ในการปฏิเสธสมมติฐานว่าง

One tailed test

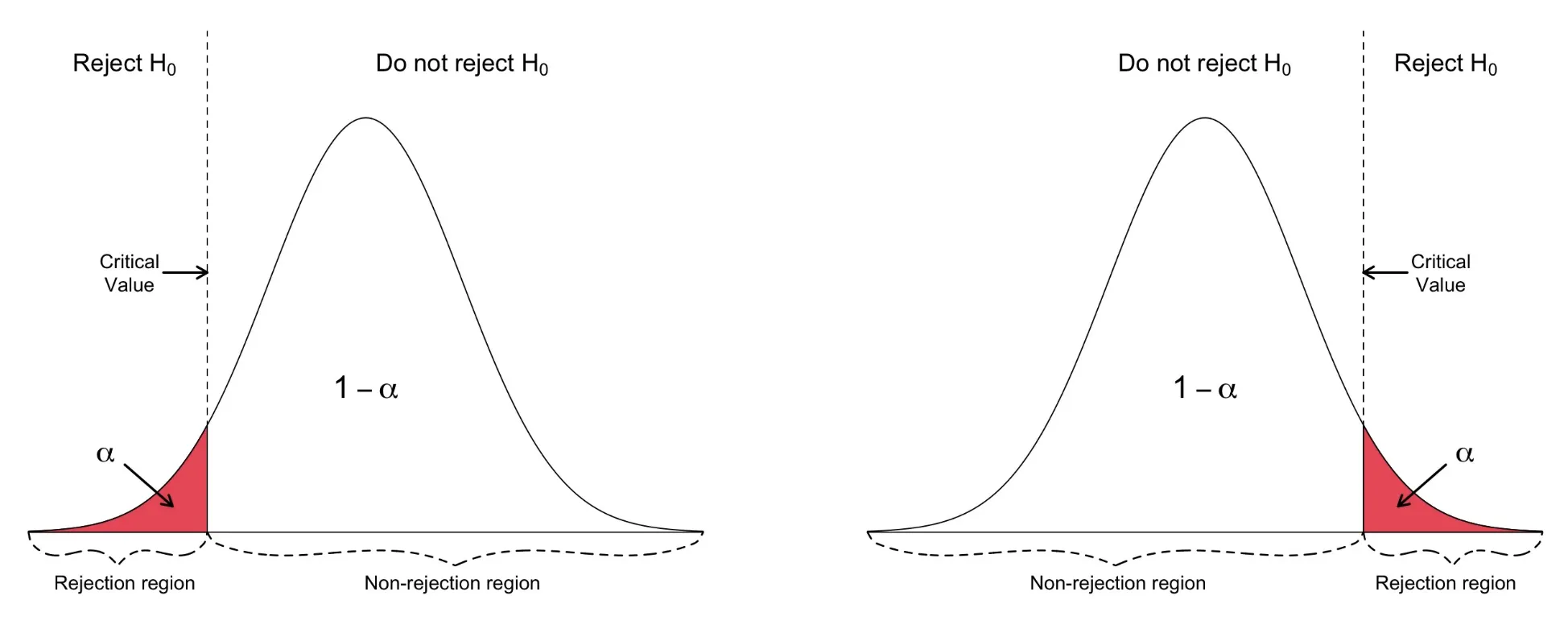
การทดสอบแบบ One-Tailed ใช้เมื่อสมมติฐานทางเลือก (H₁) ระบุถึง ทิศทาง ของผลกระทบ กล่าวคือ เรากำลังมองหาหลักฐานที่บ่งชี้ว่าพารามิเตอร์ที่สนใจมีค่า มากกว่า หรือ น้อยกว่า ค่าใดค่าหนึ่ง แต่จะไม่สนใจทั้งสองกรณีพร้อมกัน

Critical Region: บริเวณ Critical Region จะอยู่ที่ ปลายด้านใดด้านหนึ่ง ของการแจกแจงค่าสถิติการทดสอบ (Test Statistic) ซึ่งขึ้นอยู่กับสมมติฐานทางเลือก เช่น หากสมมติฐานระบุว่า “มากกว่า” บริเวณนี้จะอยู่ที่ ปลายขวา แต่หากระบุว่า “น้อยกว่า” บริเวณนี้จะอยู่ที่ ปลายซ้าย
โดยปกติ เราจะใช้การทดสอบแบบ One-Tailed เมื่อเรามีเหตุผลที่ชัดเจนหรือมีข้อมูลที่เชื่อว่าผลกระทบจะเกิดในทิศทางใดทิศทางหนึ่งโดยเฉพาะ
เช่น กำลังทดสอบยาใหม่เพื่อดูว่าสามารถช่วย ลด ความดันโลหิตได้หรือไม่ โดย
- สมมติฐานว่าง (H₀) คือ ยาไม่มีผลต่อความดันโลหิต
- ขณะที่สมมติฐานทางเลือก (H₁) คือ ยาช่วย ลด ความดันโลหิต

Two tailed Test

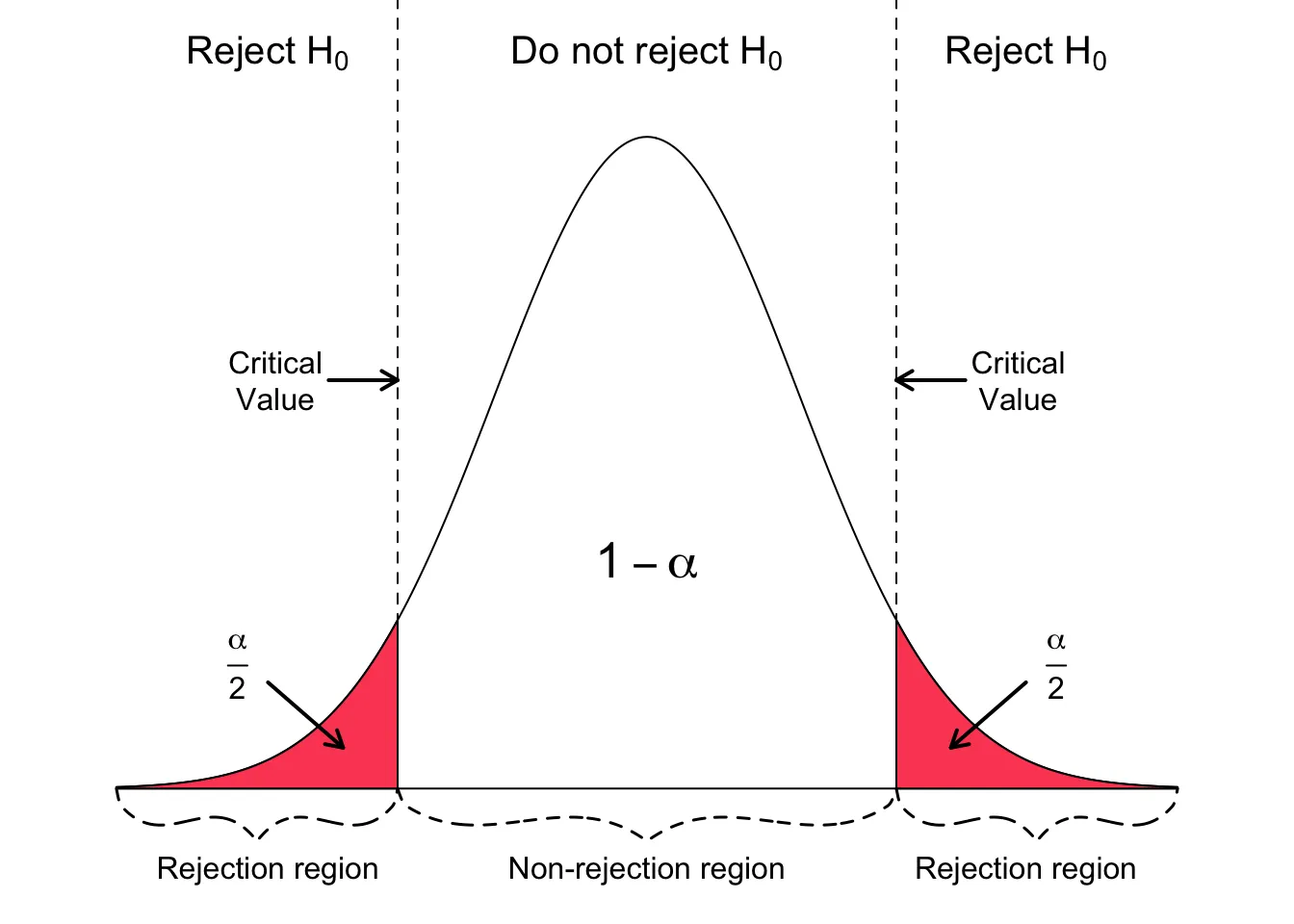
การทดสอบแบบ Two-Tailed ใช้เมื่อสมมติฐานทางเลือก (H₁) เป็นแบบ ไม่มีทิศทาง กล่าวคือ เรากำลังมองหาหลักฐานที่บ่งชี้ว่าพารามิเตอร์ที่สนใจ แตกต่าง จากค่าที่กำหนดไว้ โดยไม่ได้ระบุว่าจะมากกว่าหรือน้อยกว่า

Critical Region: บริเวณ Critical Region จะแบ่งออกเป็น สองปลาย ของการแจกแจงค่าสถิติการทดสอบ และแต่ละปลายจะมีพื้นที่เท่ากัน
โดยปกติ ใช้การทดสอบแบบ Two-Tailed เมื่อคุณสนใจตรวจสอบความแตกต่างในทุกรูปแบบโดยไม่คำนึงถึงทิศทาง
เช่น ต้องการเปรียบเทียบคะแนนความพึงพอใจของสินค้าระหว่างชายและหญิง โดยไม่มีการคาดการณ์ล่วงหน้าว่ากลุ่มใดจะให้คะแนนสูงกว่ากัน ดังนั้น คุณจะใช้การทดสอบแบบ Two-Tailed เพื่อตรวจสอบว่า มีความแตกต่าง ใด ๆ ในคะแนนความพึงพอใจหรือไม่

ดังนั้น การจะเลือกใช้ One-Tailed และ Two-Tailed Test จะขึ้นอยู่กับ

คำถามการวิจัย: ปัจจัยที่สำคัญที่สุดคือคำถามการวิจัยที่เราต้องการตอบ เรากำลังมองหาหลักฐานของผลกระทบในทิศทางใดทิศทางหนึ่งโดยเฉพาะ หรือเพียงแค่ต้องการตรวจสอบว่ามีความแตกต่างหรือไม่?
ความรู้เบื้องต้น: หากเรามีความรู้หรือเหตุผลเชิงทฤษฎีที่แข็งแรงซึ่งชี้ว่า ผลกระทบจะเกิดในทิศทางใดทิศทางหนึ่ง การทดสอบแบบ One-Tailed อาจเหมาะสมกว่า
ผลกระทบของความผิดพลาด: พิจารณาผลกระทบของข้อผิดพลาดแบบที่ 1 (Type I Error) และข้อผิดพลาดแบบที่ 2 (Type II Error) การทดสอบแบบ One-Tailed จะเพิ่มโอกาสในการตรวจพบผลกระทบในทิศทางที่กำหนดไว้ แต่จะลดโอกาสในการตรวจพบผลกระทบในทิศทางตรงกันข้าม

จากนี้เราจะขอยกตัวอย่างการทดสอบสถิติทั้งแบบฉบับคำนวณสดและแบบ python code คู่กัน เพื่อให้เห็นภาพการใข้งานมากขึ้น โดยจะเน้นไปที่ตัวอย่างทั้ง 3 แบบคือ

One sample test (ทดสอบกลุ่มเดียว)
Independent sample test (สองกลุ่มไม่ขึ้นกัน)
Paired sample test (สองกลุ่มสัมพันธ์กัน)

สถาณการณที่ 1: One-Sample

t-test เป็นการทดสอบสมมติฐานทางสถิติที่ใช้ในการเปรียบเทียบค่าเฉลี่ยของกลุ่มตัวอย่าง โดยเฉพาะอย่างยิ่งเมื่อเราไม่ทราบค่าเบี่ยงเบนมาตรฐานของประชากร และ/หรือ ขนาดตัวอย่างมีขนาดเล็ก

โดย t-test จะคำนวณสิ่งที่เรียกว่า "t-statistic" ซึ่งเป็นค่าที่บ่งบอกถึงความแตกต่างระหว่างค่าเฉลี่ยของกลุ่มตัวอย่างกับค่าเฉลี่ยที่กำหนด (ในการทดสอบแบบหนึ่งกลุ่มตัวอย่าง) หรือความแตกต่างระหว่างค่าเฉลี่ยของสองกลุ่มตัวอย่าง (ในการทดสอบแบบสองกลุ่มตัวอย่าง) จากนั้น ค่า t-statistic นี้จะถูกนำไปใช้ในการหาค่า p-value

ซึ่ง ค่า p-value ใน t-test คือความน่าจะเป็นที่จะได้ผลลัพธ์ที่สังเกตได้ (เช่น ความแตกต่างของค่าเฉลี่ย) หรือผลลัพธ์ที่รุนแรงกว่า หากสมมติฐานหลักเป็นจริง สมมติฐานหลักในการทดสอบ t-test โดยทั่วไปคือ "ไม่มีความแตกต่างระหว่างค่าเฉลี่ย”

ปัญหา: ต้องการตรวจสอบว่าความสูงเฉลี่ยของนักเรียนชั้นมัธยมศึกษาปีที่ 6 ในโรงเรียนแห่งหนึ่งสูงกว่า 165 เซนติเมตรหรือไม่
ข้อมูล: สุ่มเก็บข้อมูลความสูงของนักเรียนมา 10 คน ได้ดังนี้ (หน่วย: เซนติเมตร) 168, 170, 162, 175, 165, 172, 160, 178, 163, 171
สมมติฐาน:
- H₀: μ = 165 (ความสูงเฉลี่ยเท่ากับ 165 ซม.)
- H₁: μ > 165 (ความสูงเฉลี่ยมากกว่า 165 ซม.)
- ระดับนัยสำคัญ: α = 0.05
วิธีคำนวณ (อย่างง่าย):
1. คำนวณค่าเฉลี่ยของตัวอย่าง (x̄)
$\bar{x} = \frac{168 + 170 + 162 + 175 + 165 + 172 + 160 + 178 + 163 + 171}{10} = 168.4$
1. คำนวณส่วนเบี่ยงเบนมาตรฐานของตัวอย่าง (s)
$s = \sqrt{\frac{\sum_{i=1}^n (x_i - \bar{x})^2}{n-1}} = \sqrt{\frac{310.2}{10-1}}$ $s = \sqrt{\frac{310.2}{9}} = \sqrt{34.47} \approx 5.87$
1. คำนวณค่า t
$t = \frac{\bar{x} - \mu}{\frac{s}{\sqrt{n}}} = \frac{168.4 - 165}{\frac{5.87}{\sqrt{10}}} \approx 1.83$
1. หากำหนดองศาอิสระ (degree of freedom, df): df = n - 1 = 10 - 1 = 9
2. หาค่าวิกฤต (Critical Value) จากตาราง t-distribution ที่ระดับนัยสำคัญ α = 0.05 และ df = 9 (ประมาณ 1.833)

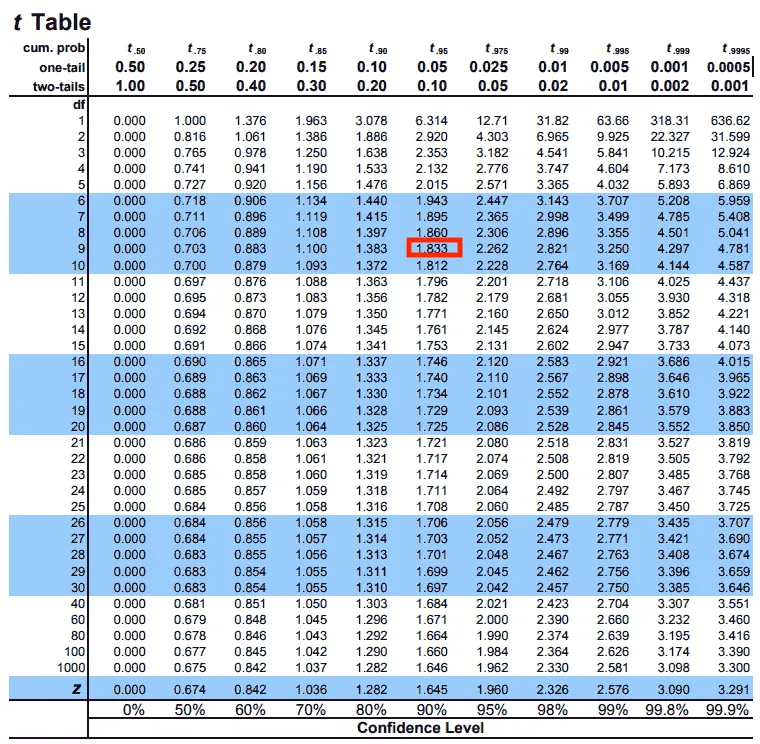
การตีความ
- เนื่องจากค่า t ที่คำนวณได้ (1.83) น้อยกว่าค่าวิกฤต (1.833) = เราจึงไม่ปฏิเสธ H₀ นั่นคือ ข้อมูลไม่เพียงพอที่จะสรุปว่าความสูงเฉลี่ยของนักเรียนสูงกว่า 165 เซนติเมตร [การทดสอบ The Critical Value เป็นแบบ One-Sample t-test (One-Tailed)]
- หรือ p value สามารถหาได้จากการนำค่า Critical value ไปคำนวน CDF ออกมา ก็จะได้ค่าออกมาราวๆ 0.049 ซึ่งยังคงน้อยกว่า 0.05 อยู่ดี
$p\text{-value} = 1 - \text{CDF}(t_{critical})$

เทียบเป็น code

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# ข้อมูลความสูงของนักเรียน
heights = np.array([168, 170, 162, 175, 165, 172, 160, 178, 163, 171])

# ค่าเฉลี่ยที่ต้องการทดสอบ (μ)
mu = 165

# ทำการทดสอบ One-Sample t-test
t_statistic, p_value = stats.ttest_1samp(heights, mu)

# เนื่องจากเป็นการทดสอบทางเดียว (greater than) ให้หาร p-value ด้วย 2 และพิจารณาเฉพาะด้านขวา
p_value_one_tailed = p_value / 2

# พิมพ์ผลลัพธ์
print("t-statistic:", t_statistic)
print("p-value (one-tailed):", p_value_one_tailed)

# กำหนดระดับนัยสำคัญ (alpha)
alpha = 0.05
df = len(heights) - 1  # จำนวนองศาอิสระ (degree of freedom)

# Critical t-value สำหรับทดสอบทางเดียว
t_critical = stats.t.ppf(1 - alpha, df)

# ตรวจสอบสมมติฐาน
if p_value_one_tailed < alpha:
    print("ปฏิเสธ H0: ความสูงเฉลี่ยของนักเรียนสูงกว่า 165 เซนติเมตร")
else:
    print("ไม่ปฏิเสธ H0: ข้อมูลไม่เพียงพอที่จะสรุปว่าความสูงเฉลี่ยสูงกว่า 165 เซนติเมตร")

# -------------------------------------------
# วาดกราฟ t-distribution
x = np.linspace(-4, 4, 1000)  # ขอบเขตการวาดกราฟ
y = stats.t.pdf(x, df)        # ค่าความน่าจะเป็นจาก t-distribution

# สร้างกราฟ
plt.figure(figsize=(10, 6))
plt.plot(x, y, label=f"t-Distribution (df={df})", color='blue')

# Highlight พื้นที่ critical region
x_critical = np.linspace(t_critical, 4, 100)
y_critical = stats.t.pdf(x_critical, df)
plt.fill_between(x_critical, y_critical, alpha=0.5, color='red', label='Critical Region (α = 0.05)')

# เส้นค่า t-statistic
plt.axvline(t_statistic, color='green', linestyle='--', label=f"t-statistic = {t_statistic:.2f}")

# เส้น critical t-value
plt.axvline(t_critical, color='red', linestyle='--', label=f"t-critical = {t_critical:.2f}")

# ตกแต่งกราฟ
plt.title("One-Sample t-Test: t-Distribution")
plt.xlabel("t-value")
plt.ylabel("Probability Density")
plt.legend()
plt.grid()
plt.show()

ผลลัพธ์ที่ได้

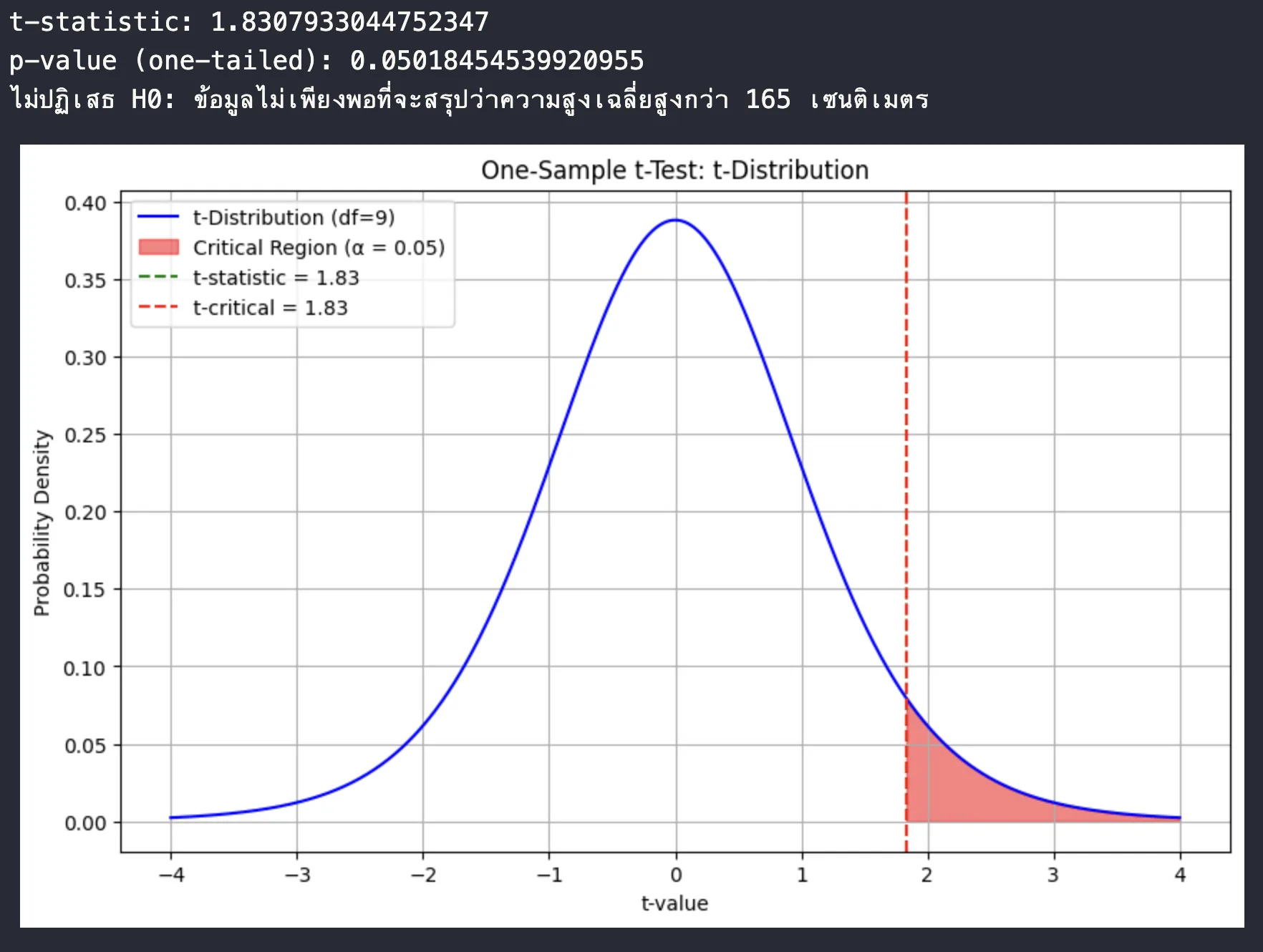
สถานการณ์ที่ 2: Independent Samples

สถานการณ์: ต้องการเปรียบเทียบความพึงพอใจต่อผลิตภัณฑ์ใหม่ระหว่างผู้ชายและผู้หญิง

ข้อมูล: สุ่มเลือกผู้ชาย 10 คน และผู้หญิง 12 คน ให้คะแนนความพึงพอใจ (1-5 โดย 1 คือไม่พอใจมากที่สุด และ 5 คือพอใจมากที่สุด) ได้ผลดังนี้

ผู้ชาย: 3, 4, 2, 4, 5, 3, 3, 4, 2, 3
ผู้หญิง: 4, 5, 4, 4, 3, 5, 4, 5, 3, 4, 4, 5

สมมติฐาน:

H₀: การกระจายตัวของความพึงพอใจระหว่างผู้ชายและผู้หญิงไม่แตกต่างกัน
H₁: การกระจายตัวของความพึงพอใจระหว่างผู้ชายและผู้หญิงแตกต่างกัน

วิธีการคำนวณ: ในตัวอย่างนี้ เนื่องจากข้อมูลเป็นแบบ ordinal (เรียงลำดับ) และเราต้องการเปรียบเทียบการกระจายตัว เราจะใช้ Mann-Whitney U test ซึ่งเป็นการทดสอบแบบ Non-parametric ที่เหมาะสม

ขั้นตอนการคำนวณแบบง่าย (Manual calculation for demonstration):

1. ข้อมูลที่ให้มา

คะแนนความพึงพอใจของ ผู้ชาย (men_scores): [3, 4, 2, 4, 5, 3, 3, 4, 2, 3]
คะแนนความพึงพอใจของ ผู้หญิง (women_scores): [4, 5, 4, 4, 3, 5, 4, 5, 3, 4, 4, 5]

จำนวนข้อมูล

$n_1 = 10$ (ผู้ชาย)
$n_2 = 12$ (ผู้หญิง)

2. ขั้นตอนการคำนวณ U Statistic โดยรวมข้อมูลทั้งสองกลุ่มและเรียงลำดับจากน้อยไปมาก ให้ Rank ข้อมูลโดย: ค่าซ้ำจะได้ Rank เฉลี่ยของตำแหน่งนั้น ๆ

Observation	2	3	4	5
Rank	1.5	6.5	12	18.5

หาผลรวมของ Rank (R) ของแต่ละกลุ่ม

Rank ของผู้ชาย (W₁): รวม Rank ของผู้ชาย

W₁ = 1.5 + 1.5 + 6.5 + 6.5 + 6.5 + 6.5 + 12 + 12 + 12 + 18.5 = 83.5

Rank ของผู้หญิง (W₂): รวม Rank ของผู้หญิง

W₂ = 6.5 + 12 + 12 + 12 + 12 + 12 + 12 + 18.5 + 18.5 + 18.5 + 18.5 + 18.5 = 171

คำนวณค่า U Statistic โดยใช้สูตร

U_1 = w_1 - \frac{n_1(n_1 + 1)}{2}

U_2 = w_2 - \frac{n_2(n_2 + 1)}{2}

โดยที่

$n_1 = 10$ , $n_2 = 12$ , $R_1 = 57.5$ , $R_2 = 152.5$

ทำการคำนวน $U_1$ , $U_2$

U_1 = 83.5 - \frac{10(10 + 1)}{2} = 28.5

U_2 = 171 - \frac{12(12 + 1)}{2} = 92

เลือกค่า U ที่น้อยที่สุด

ค่า U ที่ได้จากการคำนวณจะมี 2 ค่า $U_1 = 29.0$ , $U_2 = 92$
ดังนั้น U Statistic = 29.0 (เลือกค่าน้อยสุด)

หาค่า p-value จาก U Statistic

ทำได้โดย

เทียบค่า U Statistic กับการแจกแจงค่าของ Mann-Whitney U ซึ่งมีลักษณะใกล้เคียงกับการแจกแจงแบบปกติ เมื่อ $n_1$ , $n_2$ มีขนาดเพียงพอ
เริ่มต้นจากการหา Critical Value ของ Mann-Whitney U จากตาราง (0.05 แบบ two-tailed)

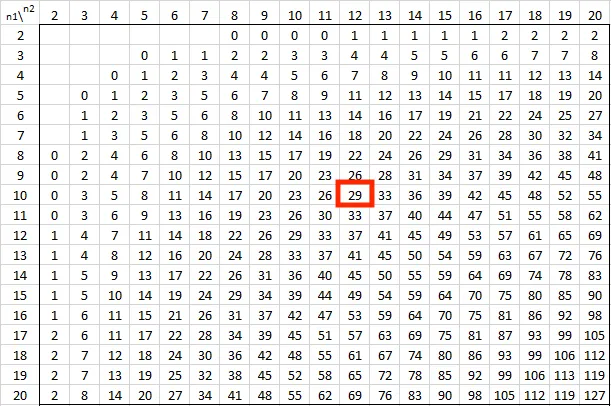
Ref: https://real-statistics.com/statistics-tables/mann-whitney-table/

ซึ่งหมายความว่า
- ถ้า $U \leq 29$ : เราปฏิเสธ $H_0$ (มีความแตกต่างอย่างมีนัยสำคัญ)
- ถ้า $U > 29$ : ไม่สามารถปฏิเสธ $H_0$ ได้
ดังนั้น เราจึงได้ข้อสรุปว่า "มีความแตกต่างอย่างมีนัยสำคัญทางสถิติระหว่างการกระจายตัวของผู้ชายและผู้หญิง” เนื่องจากสามารถปฏิเสธ $H_0$ ได้

code python

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import mannwhitneyu, norm

# ข้อมูลคะแนนความพึงพอใจ
men_scores = [3, 4, 2, 4, 5, 3, 3, 4, 2, 3]
women_scores = [4, 5, 4, 4, 3, 5, 4, 5, 3, 4, 4, 5]

# การคำนวณ Mann-Whitney U Test
u_stat, p_value = mannwhitneyu(men_scores, women_scores, alternative='two-sided')

# แสดงผลลัพธ์การทดสอบ
print(f"U Statistic: {u_stat:.2f}")
print(f"P-Value: {p_value:.4f}")

if p_value < 0.05:
    print("สรุป: มีความแตกต่างอย่างมีนัยสำคัญทางสถิติระหว่างการกระจายตัวของผู้ชายและผู้หญิง")
else:
    print("สรุป: ไม่มีความแตกต่างอย่างมีนัยสำคัญทางสถิติระหว่างการกระจายตัวของผู้ชายและผู้หญิง")

# การคำนวณสำหรับการตีกราฟ Two-Tailed Test
alpha = 0.05
critical_value = norm.ppf(1 - alpha / 2)
z_score = norm.ppf(1 - p_value / 2)

x = np.linspace(-4, 4, 1000)
y = norm.pdf(x, 0, 1)

# แสดงการกระจายตัวข้อมูลด้วยกราฟ
plt.figure(figsize=(15, 6))

# Histogram
plt.subplot(1, 3, 1)
plt.hist(men_scores, bins=np.arange(1.5, 6.5, 1), alpha=0.7, label='Men', color='blue')
plt.hist(women_scores, bins=np.arange(1.5, 6.5, 1), alpha=0.7, label='Women', color='orange')
plt.title('Distribution of Satisfaction Scores')
plt.xlabel('Satisfaction Score')
plt.ylabel('Number of Participants')
plt.legend()

# Boxplot
plt.subplot(1, 3, 2)
plt.boxplot([men_scores, women_scores], labels=['Men', 'Women'])
plt.title('Boxplot of Satisfaction Scores')
plt.ylabel('Satisfaction Score')

# P-value graph
plt.subplot(1, 3, 3)
plt.plot(x, y, label="Normal Distribution")
plt.axvline(critical_value, color='red', linestyle='--', label='Critical Value (Right)')
plt.axvline(-critical_value, color='red', linestyle='--', label='Critical Value (Left)')
plt.axvline(z_score, color='blue', linestyle='-', label=f'Z-Score (P-Value) = {z_score:.2f}')
plt.fill_between(x, y, where=(x > critical_value) | (x < -critical_value), color='red', alpha=0.2)
plt.title('Two-Tailed Test: Critical Values and P-Value')
plt.xlabel('Z-Score')
plt.ylabel('Probability Density')
plt.legend()

plt.tight_layout()
plt.show()

ผลลัพธ์

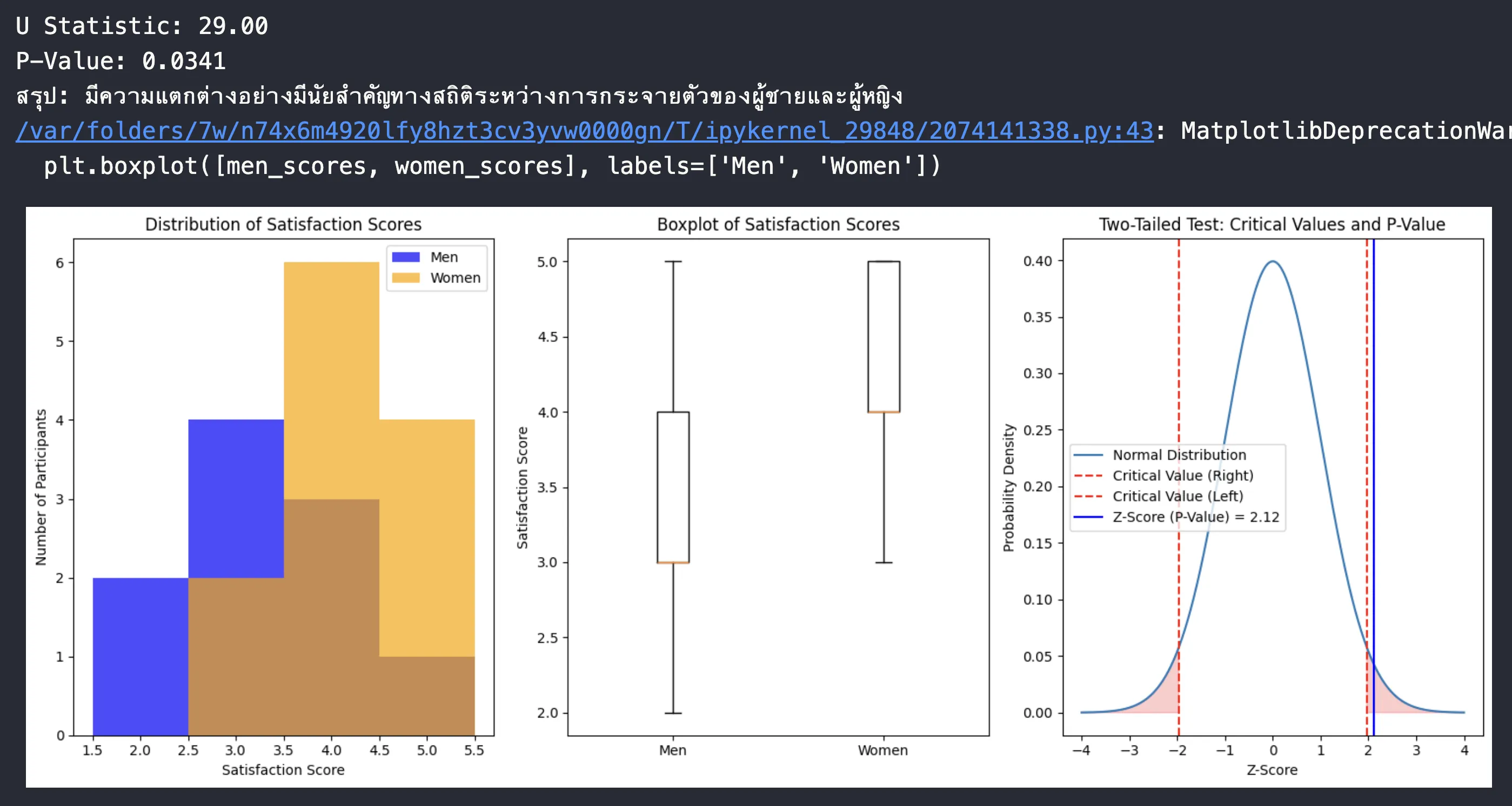
Note

เนื่องจากขนาดกลุ่มตัวอย่าง $n_1 = 10$ และ $n_2 = 12$ เพียงพอต่อการใช้ Normal Approximation ตามหลัก Central Limit Theorem
การแจกแจงของ U-Statistic จึงถูกประมาณด้วย Normal Distribution ซึ่งช่วยให้คำนวณค่า Critical Value และ Z-Statistic ได้ง่ายขึ้น

สถานการณ์ที่ 3: Paired Samples

สถานการณ์: ต้องการทดสอบว่าการฝึกอบรมทักษะการพูดในที่สาธารณะช่วยลดความประหม่าได้จริงหรือไม่ (เช่นเดียวกับโจทย์เดิม)
ข้อมูล: วัดระดับความประหม่าของผู้เข้ารับการอบรม 12 คน ก่อนและหลังการอบรม (คะแนนยิ่งสูง แสดงว่าประหม่ามาก)
- ก่อนอบรม: 8, 10, 7, 9, 11, 6, 8, 9, 7, 10, 9, 8
- หลังอบรม: 6, 7, 5, 7, 8, 4, 6, 7, 5, 8, 7, 6
สมมติฐาน:
- H₀: การฝึกอบรมไม่มีผลต่อระดับความประหม่า (ความแตกต่างของคะแนนก่อนและหลังอบรมมีการกระจายตัวแบบสมมาตร รอบค่ามัธยฐานเป็นศูนย์)
- H₁: การฝึกอบรมมีผลต่อระดับความประหม่า (ความแตกต่างของคะแนนก่อนและหลังอบรมไม่ได้มีการกระจายตัวแบบสมมาตร รอบค่ามัธยฐานเป็นศูนย์) โดยเฉพาะคือมีแนวโน้มที่จะลดลง

ขอเสนอตัวอย่างการคำนวณสถิติแบบ Paired Samples ที่คล้ายกับโจทย์ของคุณ โดยใช้วิธีการทดสอบ Wilcoxon Signed-Rank Test ซึ่งเป็นวิธีการทดสอบแบบ Non-parametric ที่เหมาะสมกับข้อมูลแบบ Paired Samples และไม่จำเป็นต้องมีข้อตกลงเบื้องต้นว่าข้อมูลมีการแจกแจงแบบปกติ

การทดสอบสถิติแบบ Wilcoxon Signed-Rank Test

ขั้นตอนการทดสอบ Wilcoxon Signed-Rank Test สำหรับข้อมูลแบบจับคู่ (ก่อนและหลัง):

1. คำนวณความแตกต่างของคะแนน

สำหรับแต่ละคู่ข้อมูล คำนวณ

d_i = X_{\text{ก่อน}} - X_{\text{หลัง}}

โดยที่ $X_{\text{ก่อน}}$ คือคะแนนก่อนการอบรม และ $X_{\text{หลัง}}$ คือคะแนนหลังการอบรม

| ลำดับที่ (คนที่) | คะแนนก่อนอบรม | คะแนนหลังอบรม | ผลต่าง (คะแนนเพิ่ม/ลด) $d_i$ | ค่าสัมบูรณ์ของผลต่าง $|d_i|$ | | --- | --- | --- | --- | --- | | 1 | 8 | 6 | 2 | 2 | | 2 | 10 | 7 | 3 | 3 | | 3 | 7 | 5 | 2 | 2 | | 4 | 9 | 7 | 2 | 2 | | 5 | 11 | 8 | 3 | 3 | | 6 | 6 | 4 | 2 | 2 | | 7 | 8 | 6 | 2 | 2 | | 8 | 9 | 7 | 2 | 2 | | 9 | 7 | 5 | 2 | 2 | | 10 | 10 | 8 | 2 | 2 | | 11 | 9 | 7 | 2 | 2 | | 12 | 8 | 6 | 2 | 2 |

2. ตัดค่าความแตกต่างที่เป็น 0 ออก —> ในกรณีนี้ ทุกค่าของ $d_i \neq 0$ ดังนั้นไม่ต้องตัดค่าใดออก

จัดลำดับอันดับ (Ranks) ของค่าความแตกต่างแบบสัมบูรณ์ ( $|d_i|$ )

เรียงลำดับ $|d_i|$ จากค่าน้อยไปหามาก พร้อมให้ลำดับที่เหมาะสม (กรณีมีค่าซ้ำต้องเฉลี่ยลำดับ)

| $|d_i|$ | Rank | | --- | --- | | 2 | 1.5 | | 2 | 1.5 | | 2 | 1.5 | | 2 | 1.5 | | 2 | 1.5 | | 2 | 1.5 | | 2 | 1.5 | | 2 | 1.5 | | 2 | 1.5 | | 2 | 1.5 | | 3 | 11 | | 3 | 11 |

4. บวกลำดับแยกเป็นสองส่วน:

$W^+$ : ผลรวมของลำดับที่มี $d_i > 0$
$W^-$ : ผลรวมของลำดับที่มี $d_i < 0$

ในกรณีนี้ ค่าความแตกต่างทั้งหมดเป็นบวก ( $d_i > 0$ ):

ผลรวมลำดับ $W^+ = 1.5 + 1.5 + 1.5 + 1.5 + 1.5 + 1.5 + 1.5 + 1.5 + 1.5 + 1.5 + 11 + 11 = 37.5$
ผลรวมลำดับ $W^- = 0$ เพราะไม่มีค่าที่ $d_i < 0$

5. เลือกค่าสถิติที่เล็กกว่าเป็น W: $W = \min(W^+, W^-) = 0$

6. ค่าความน่าจะเป็น $pValue$ (เปรียบเทียบกับ $\alpha$ )

ใช้ตารางค่าสถิติ Wilcoxon Signed-Rank สำหรับ n = 12 และ W = 0

จากตาราง Value ที่ระดับนัยสำคัญ $\alpha = 0.05$ สำหรับ n = 12 จะมีค่าเทียบได้ ดังนี้ (เป็นแบบ one test)

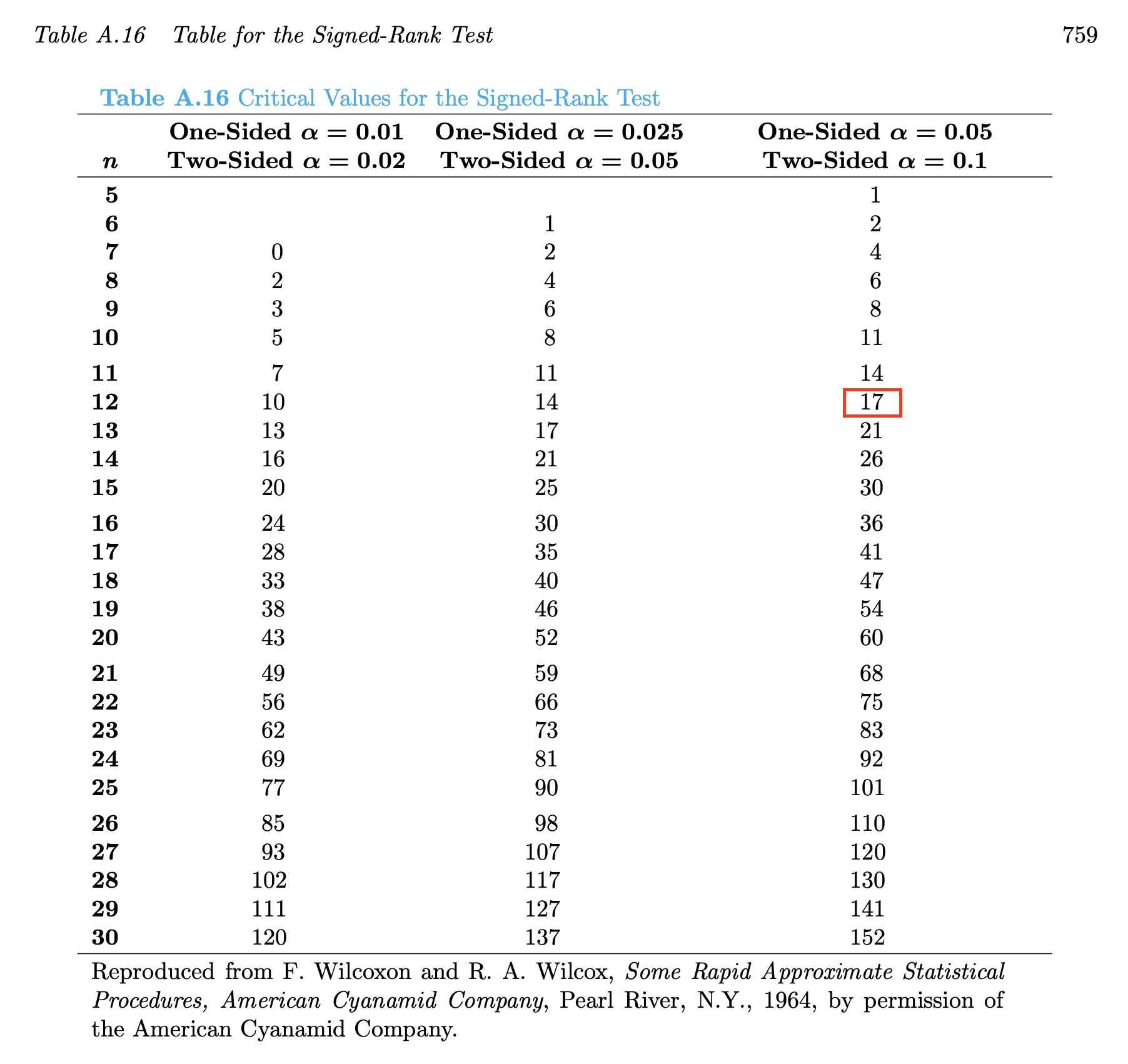
Ref: https://real-statistics.com/statistics-tables/wilcoxon-signed-ranks-table/

เนื่องจาก W < 17 เราจึงปฏิเสธ H₀ นั่นคือ ยอมรับ H₁ สรุปได้ว่า การฝึกอบรมมีผลต่อการลดระดับความประหม่า อย่างมีนัยสำคัญทางสถิติ

code python

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import wilcoxon, norm

# ข้อมูล: คะแนนระดับความประหม่า ก่อนและหลังการอบรม
before_training = np.array([8, 10, 7, 9, 11, 6, 8, 9, 7, 10, 9, 8])
after_training = np.array([6, 7, 5, 7, 8, 4, 6, 7, 5, 8, 7, 6])

# คำนวณความแตกต่าง (Before - After)
differences = before_training - after_training

# ทำการทดสอบ Wilcoxon Signed-Rank Test (one-tailed, ลดลง)
w_stat, p_value = wilcoxon(differences, alternative='greater')

# คำนวณ Critical Value สำหรับ Wilcoxon Distribution
n = len(differences)
alpha = 0.05

# หา Critical Z-Value
z_critical = norm.ppf(1 - alpha)
z_stat = (w_stat - n * (n + 1) / 4) / np.sqrt(n * (n + 1) * (2 * n + 1) / 24)

# แสดงผลลัพธ์
print("ผลการทดสอบ Wilcoxon Signed-Rank Test")
print(f"ความแตกต่างของคะแนน (Before - After): {differences}")
print(f"Wilcoxon W-Statistic: {w_stat:.2f}")
print(f"Z-Statistic (Approximation): {z_stat:.2f}")
print(f"P-Value (one-tailed): {p_value:.4f}")

if p_value < alpha:
    print("สรุป: ปฏิเสธ H₀ -> การฝึกอบรมช่วยลดความประหม่าได้อย่างมีนัยสำคัญ")
else:
    print("สรุป: ไม่ปฏิเสธ H₀ -> ไม่มีหลักฐานเพียงพอว่าการฝึกอบรมช่วยลดความประหม่า")

# -------------------------------------------
# การแสดงผลกราฟ
plt.figure(figsize=(15, 6))

# 1. การแจกแจงข้อมูลก่อนและหลัง
plt.subplot(1, 3, 1)
plt.hist(before_training, bins=5, alpha=0.7, label='Before Training', color='blue')
plt.hist(after_training, bins=5, alpha=0.7, label='After Training', color='orange')
plt.title("Distribution of Anxiety Scores")
plt.xlabel("Anxiety Score")
plt.ylabel("Frequency")
plt.legend()

# 2. Boxplot เปรียบเทียบข้อมูล
plt.subplot(1, 3, 2)
plt.boxplot([before_training, after_training], tick_labels=["Before Training", "After Training"])
plt.title("Boxplot of Anxiety Scores")
plt.ylabel("Anxiety Score")

# 3. Critical Value Plot
x = np.linspace(-4, 4, 1000)
y = norm.pdf(x)
plt.subplot(1, 3, 3)
plt.plot(x, y, label="Standard Normal Distribution", color="purple")
plt.axvline(z_critical, color="red", linestyle="--", label=f"Critical Z = {z_critical:.2f}")
plt.axvline(z_stat, color="green", linestyle="--", label=f"Z-Statistic = {z_stat:.2f}")
plt.title("Wilcoxon Test: Z-Statistic and Critical Value")
plt.xlabel("Z-Value")
plt.ylabel("Density")
plt.legend()

# ตกแต่งและแสดงกราฟ
plt.tight_layout()
plt.show()

ผลลัพธ์

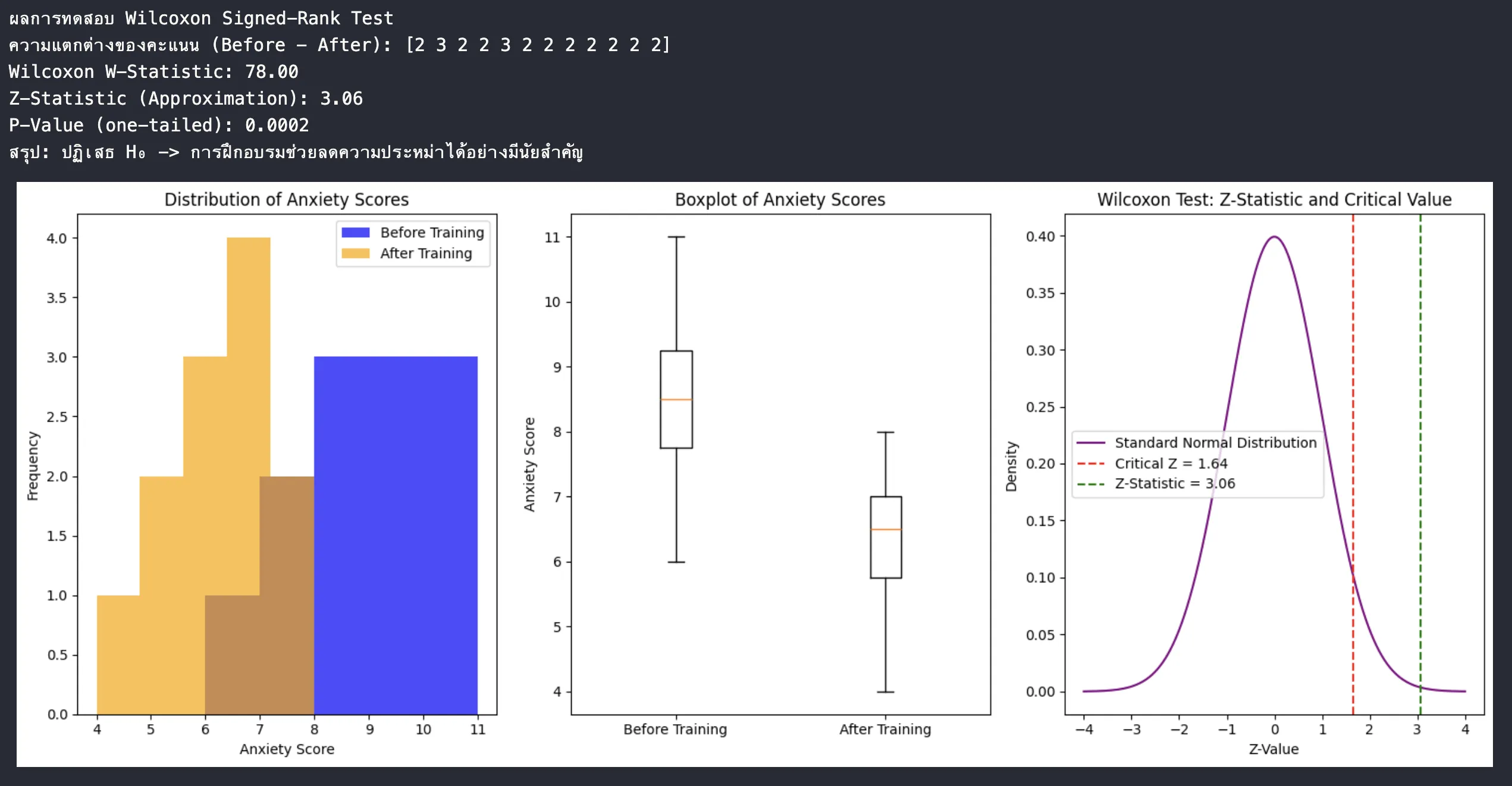
ข้อควรระวังในการทำ Hypothesis Testing

ข้อควรระวังสำคัญที่ควรพิจารณาเมื่อทำการทดสอบสมมติฐาน (Hypothesis Testing)

ความสัมพันธ์ระหว่างข้อผิดพลาดประเภทที่ 1 และประเภทที่ 2

สำหรับขนาดตัวอย่างที่คงที่ การลดความน่าจะเป็นของ Type I error (α) มักจะทำให้ความน่าจะเป็นของ Type II error (β) เพิ่มขึ้น ซึ่งหมายความว่ามีการแลกเปลี่ยนระหว่างข้อผิดพลาดทั้งสองประเภท คุณต้องพิจารณาผลกระทบของข้อผิดพลาดแต่ละประเภทในบริบทของคุณ และพยายามหาสมดุลที่ยอมรับได้

Type I Error: เกิดขึ้นเมื่อมีการ ปฏิเสธสมมติฐานศูนย์ (H₀) ทั้งที่สมมติฐานศูนย์นั้นเป็นจริง เรียกอีกอย่างว่า ผลบวกลวง (False Positive) ความน่าจะเป็นที่จะเกิด Type I Error ถูกแทนด้วยอักษรกรีก α (alpha) ซึ่งเรียกอีกอย่างว่า ระดับนัยสำคัญ (Level of Significance) หรือ ขนาดของการทดสอบ (Size of the Test)
Type II Error: เกิดขึ้นเมื่อมีการ ไม่ปฏิเสธสมมติฐานศูนย์ (H₀) ทั้งที่สมมติฐานศูนย์นั้นเป็นเท็จ เรียกอีกอย่างว่า ผลลบลวง (False Negative) ความน่าจะเป็นที่จะเกิด Type II Error ถูกแทนด้วยอักษรกรีก β (beta)

หรือถ้าพูดแบบง่ายๆ

Type I Error: คุณคิดว่าค้นพบผลลัพธ์ที่แท้จริง แต่จริง ๆ แล้วมันเกิดจากความบังเอิญ
Type II Error: คุณพลาดผลลัพธ์ที่แท้จริงเพราะมันไม่ปรากฏชัดในข้อมูลของคุณ

ผลกระทบของขนาดตัวอย่าง

การเพิ่มขนาดตัวอย่าง (n) สามารถลดทั้ง α และ β ได้พร้อมกัน ขนาดตัวอย่างที่มากขึ้นช่วยให้ได้ข้อมูลมากขึ้นและนำไปสู่การทดสอบที่มีประสิทธิภาพมากขึ้น อย่างไรก็ตาม ก็ต้องแลกกับต้นทุน (เวลาและทรัพยากร) คุณต้องหาขนาดตัวอย่างที่สมดุลระหว่างพลังทางสถิติกับข้อจำกัดในทางปฏิบัติ

ความสำคัญของการกำหนดค่า α ก่อนที่จะดูข้อมูล

การเลือกระดับนัยสำคัญ (α) หลังจาก ดูผลลัพธ์แล้ว อาจทำให้เกิดความลำเอียงและนำไปสู่ข้อสรุปที่ผิดพลาด คุณอาจถูกล่อลวงให้ปรับค่า α เพื่อให้ผลลัพธ์ดูมีนัยสำคัญมากกว่าที่เป็นจริง ดังนั้นควรกำหนดค่า α ล่วงหน้า โดยพิจารณาจากบริบทของการวิจัยและระดับความเสี่ยงที่ยอมรับได้สำหรับ Type I error

สมมติฐานของการทดสอบ

การทดสอบสมมติฐานเชิงพาราเมตริก (Parametric Hypothesis Tests) ส่วนใหญ่ เช่น t-test อาศัยสมมติฐานเกี่ยวกับการกระจายของประชากร (เช่น การกระจายตัวแบบปกติ) หากสมมติฐานเหล่านี้ถูกละเมิด อาจส่งผลต่อความถูกต้องของผลการทดสอบ

ควรตรวจสอบสมมติฐานของการทดสอบที่คุณใช้งานเสมอ หากสมมติฐานไม่ตรง อาจจำเป็นต้องใช้ Nonparametric Test ที่ไม่อาศัยสมมติฐานเกี่ยวกับการกระจายตัวของข้อมูล

ตัวอย่างเช่น หากคุณใช้ตัวอย่างขนาดเล็กและข้อมูลไม่ได้กระจายตัวแบบปกติ Wilcoxon Signed-Rank Test อาจเป็นทางเลือกที่เหมาะสมกว่าการใช้ t-test ดังที่ได้กล่าวถึงในบทสนทนาก่อนหน้า

การตีความค่า P-value อย่างระมัดระวัง

P-value ให้ข้อมูลเกี่ยวกับความแข็งแกร่งของหลักฐานที่ขัดแย้งกับสมมติฐานศูนย์ (Null Hypothesis) แต่ไม่ได้บอกความน่าจะเป็นว่าสมมติฐานศูนย์เป็นจริง ค่า P-value ที่ต่ำบ่งชี้ว่าผลลัพธ์ที่สังเกตได้นั้นไม่น่าจะเกิดขึ้นหากสมมติฐานศูนย์เป็นจริง แต่ไม่ได้รับประกันว่าสมมติฐานทางเลือก (Alternative Hypothesis) เป็นจริง

ความแตกต่างระหว่างการไม่ปฏิเสธ H₀ และการยอมรับ H₀

การไม่ปฏิเสธสมมติฐานศูนย์ ไม่ได้หมายความว่า สมมติฐานศูนย์เป็นจริง แต่หมายความว่าไม่มีหลักฐานเพียงพอที่จะปฏิเสธสมมติฐานศูนย์