Probability

Probability Distributions คืออะไร

Probability Distributions (การแจกแจงความน่าจะเป็น) คือ ฟังก์ชันหรือการแจกแจงที่แสดงถึงความน่าจะเป็นของค่าที่เป็นไปได้ในชุดข้อมูลหรือเหตุการณ์ ตัวอย่างที่เห็นได้ชัด เช่น การโยนเหรียญ การทอยลูกเต๋า หรือการวัดอุณหภูมิในแต่ละวัน การแจกแจงเหล่านี้สามารถบอกได้ว่าค่าบางค่ามีแนวโน้มเกิดขึ้นมากน้อยเพียงใด

ประเภทของ Probability Distributions ที่สำคัญ

1. Discrete Distributions (ข้อมูลไม่ต่อเนื่อง)

การแจกแจงความน่าจะเป็นที่ใช้กับข้อมูลที่มีลักษณะ ไม่ต่อเนื่อง หรือค่าที่สามารถนับได้อย่างชัดเจน เช่น จำนวนเต็มหรือเหตุการณ์ที่เกิดขึ้นเป็นจำนวนครั้ง เช่น การโยนเหรียญที่ผลลัพธ์มีได้แค่ "หัว" หรือ "ก้อย" หรือจำนวนลูกค้าที่เข้าร้านในแต่ละวัน ตัวอย่างของ Discrete Distributions ที่พบได้บ่อยคือ Binomial Distribution ซึ่งใช้วิเคราะห์ความน่าจะเป็นของจำนวนความสำเร็จในเหตุการณ์ที่มีผลลัพธ์แค่สองแบบ (เช่น ใช่/ไม่ใช่) ในจำนวนครั้งที่กำหนด

2. Continuous Distributions (ข้อมูลต่อเนื่อง)

Continuous Distributions คือการแจกแจงความน่าจะเป็นที่ใช้กับข้อมูลที่มีลักษณะ ต่อเนื่อง หรือค่าที่สามารถวัดได้ในช่วงของตัวเลขที่ไม่มีขอบเขตที่ชัดเจน เช่น อุณหภูมิ ความยาว หรือเวลา ตัวอย่างที่พบบ่อยคือ Normal Distribution (หรือ Gaussian Distribution) ซึ่งมีกราฟรูประฆังคว่ำ แสดงการกระจายของข้อมูลที่มีแนวโน้มรวมตัวใกล้ค่าเฉลี่ยและลดลงเมื่อห่างออกไปจากค่าเฉลี่ย การแจกแจงแบบต่อเนื่องเหมาะกับการวิเคราะห์ข้อมูลที่ละเอียดและมีค่าอยู่ในช่วงที่ไม่สามารถนับได้ทีละค่า เช่น ความเร็วลมในแต่ละวัน

ประโยชน์ของ Probability Distributions ใน Data Analytics

การแจกแจงความน่าจะเป็นมีบทบาทสำคัญใน Data Analytics เพราะช่วยในการวิเคราะห์และคาดการณ์พฤติกรรมของข้อมูล รวมถึงสนับสนุนการตัดสินใจได้อย่างมีเหตุผล ตัวอย่างประโยชน์มีดังนี้:

1. การทำ Data Modeling Probability Distributions ใช้เป็นพื้นฐานสำหรับการสร้างโมเดลของข้อมูล เช่น การประมาณค่าของข้อมูลหรือการคาดการณ์ในอนาคต เช่น ใช้ Normal Distribution เพื่อคาดการณ์การกระจายตัวของยอดขายสินค้า

2. การระบุ Outliers ใช้ Distributions เช่น Normal Distribution ในการตรวจสอบว่าค่าที่อยู่นอกกรอบมีความผิดปกติ (Outlier) หรือไม่ เช่น ค่าคะแนนสอบที่สูง/ต่ำผิดปกติ

3. การสร้าง Random Sampling ใช้ Distributions ในการสร้างตัวอย่างแบบสุ่ม (Random Sample) เพื่อใช้ในงานวิจัยหรือการทดลองทางสถิติ เช่น การสุ่มตัวอย่างจาก Uniform Distribution

4. การทำ Hypothesis Testing การทดสอบสมมติฐาน (Hypothesis Testing) อาศัย Probability Distributions ในการกำหนดค่าความน่าจะเป็น เช่น การใช้ t-Distribution ในการเปรียบเทียบค่าเฉลี่ยระหว่างกลุ่มข้อมูล

5. การประเมินความเสี่ยง ในธุรกิจ Probability Distributions ช่วยในการประเมินความเสี่ยงของเหตุการณ์ต่าง ๆ เช่น การใช้ Poisson Distribution เพื่อคาดการณ์จำนวนลูกค้าที่จะเข้ามาในร้านค้าในช่วงเวลาหนึ่ง

6. การประยุกต์ใน Machine Learning หลายอัลกอริทึม เช่น Naive Bayes หรือ Gaussian Mixture Models ใช้ Probability Distributions เป็นแกนหลักในการคำนวณ

Discrete Distributions

Discrete Distributions เป็นการแจกแจงความน่าจะเป็นของตัวแปรสุ่มที่สามารถรับค่าได้เฉพาะตัวเลขที่นับได้ (เช่น จำนวนเต็ม) ตัวอย่างเช่น จำนวนครั้งที่ลูกเต๋าออกหน้า 6 ในการทอย 10 ครั้ง หรือจำนวนลูกค้าที่เข้าร้านในช่วงเวลา 1 ชั่วโมง

ตัวอย่างที่นิยมใน Discrete Distributions

• Binomial Distribution: ใช้กับเหตุการณ์ที่มีผลลัพธ์ 2 แบบ เช่น สำเร็จ/ไม่สำเร็จ
• Poisson Distribution: ใช้สำหรับการนับจำนวนเหตุการณ์ที่เกิดขึ้นในช่วงเวลาหนึ่ง เช่น จำนวนอีเมลที่ได้รับใน 1 ชั่วโมง

ยกตัวอย่างใน Python ด้วย Binomial Distribution โดยใช้ library numpy

import numpy as np
import matplotlib.pyplot as plt

# ตัวอย่าง: Binomial Distribution
# สมมติว่าเราทอยเหรียญ 10 ครั้ง โดยความน่าจะเป็นออก "หัว" เท่ากับ 0.5
n_trials = 10  # จำนวนการทอยเหรียญ
p_success = 0.5  # ความน่าจะเป็นของ "หัว"
n_simulations = 1000  # จำนวนตัวอย่าง

# สร้างข้อมูลจำลองจาก Binomial Distribution
rng = np.random.default_rng(seed=42)
data = rng.binomial(n_trials, p_success, n_simulations)

# ดูข้อมูลตัวอย่าง
print("ตัวอย่างข้อมูล:", data[:10])

# การสร้าง histogram เพื่อแสดงการกระจายตัวของข้อมูล
plt.hist(data, bins=range(n_trials + 2), align='left', rwidth=0.8, color='skyblue', edgecolor='black')
plt.title("Histogram of Binomial Distribution")
plt.xlabel("Number of successes (ออกหัว)")
plt.ylabel("Frequency")
plt.xticks(range(n_trials + 1))
plt.show()

ผลลัพธ์

• ตัวอย่างข้อมูล: [6 5 7 6 3 8 6 6 3 5]

Histogram จะแสดงว่าความน่าจะเป็นสูงสุดอยู่ใกล้ค่าเฉลี่ย (5 ในกรณีนี้) ซึ่งสอดคล้องกับทฤษฎีของ Binomial Distribution เมื่อความน่าจะเป็นของความสำเร็จเท่ากับ 0.5

Discrete Distributions เหมาะสำหรับงานที่ต้องวิเคราะห์และคาดการณ์เกี่ยวกับเหตุการณ์ที่สามารถนับได้และมีความเป็นไปได้แบบไม่ต่อเนื่อง ตัวอย่างที่ใช้ในงาน Data Analyst เช่น

• การวิเคราะห์อัตราความสำเร็จของแคมเปญการตลาด ใช้ Binomial Distribution เพื่อตรวจสอบว่าแคมเปญจะดึงดูดลูกค้าได้กี่คนจากกลุ่มเป้าหมาย
  • เช่น กำหนดให้ความสำเร็จหมายถึงลูกค้ากระทำบางอย่าง เช่น คลิกที่ลิงก์, ลงทะเบียน, หรือซื้อสินค้า โดยถ้าส่งอีเมลให้ลูกค้า 1,000 คน และมีคนตอบกลับ 200 คน ความสำเร็จคือการตอบกลับ
• การคาดการณ์จำนวนเหตุการณ์ในช่วงเวลาหนึ่ง ใช้ Poisson Distribution เพื่อตรวจสอบจำนวนลูกค้าที่อาจเข้าร้านในช่วงเวลาหนึ่ง
  • เช่น จำนวนลูกค้าที่เข้าร้านใน 1 ชั่วโมง, จำนวนการโทรเข้าศูนย์บริการใน 1 วัน

ตัวอย่างที่ 1: การคาดการณ์จำนวนลูกค้าที่เข้าร้าน

สมมติว่าเราต้องการคาดการณ์จำนวนลูกค้าที่เข้ามาในร้านต่อชั่วโมง โดยมีค่าเฉลี่ยลูกค้าเข้าร้านอยู่ที่ 5 คนต่อชั่วโมง (ใช้ Poisson Distribution)

import numpy as np
import matplotlib.pyplot as plt

# ค่าเฉลี่ยจำนวนลูกค้าเข้าร้านต่อชั่วโมง
mean_customers = 5  

# สร้างข้อมูลจำลองจาก Poisson Distribution
hours = 1000  # จำนวนชั่วโมงที่ต้องการจำลอง

# สร้าง Generator object
rng = np.random.default_rng(seed=42)

# สร้างข้อมูลจำลองโดยใช้ Generator
data = rng.poisson(mean_customers, hours)

# แสดงข้อมูลตัวอย่าง
print("ตัวอย่างจำนวนลูกค้าที่เข้าร้านต่อชั่วโมง:", data[:10])

# การสร้าง Histogram เพื่อแสดงการกระจายตัวของจำนวนลูกค้า
plt.hist(data, bins=range(0, max(data) + 2), align='left', rwidth=0.8, color='orange', edgecolor='black')
plt.title("Number of Customers Per Hour (Poisson Distribution)")
plt.xlabel("Number of Customers")
plt.ylabel("Frequency")
plt.xticks(range(0, max(data) + 1))
plt.show()

ผลลัพธ์: ตัวอย่างจำนวนลูกค้าที่เข้าร้านต่อชั่วโมง: [8 7 7 2 6 3 8 3 7 8]

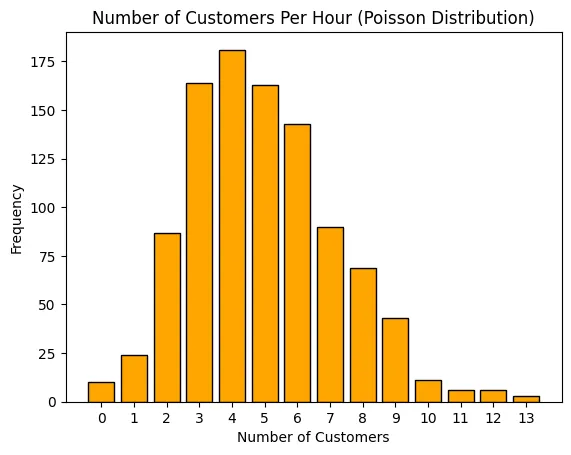
ซึ่งผลลัพธ์จาก Poisson Distribution (ลูกค้าเข้าร้าน) นี้ ก็จะช่วยคาดการณ์ว่าควรจัดเตรียมทรัพยากร (พนักงาน/สินค้า) อย่างไรในช่วงเวลาต่าง ๆ

ตัวอย่างที่ 2: การวิเคราะห์แคมเปญการตลาด

สมมติว่ามีแคมเปญที่ส่งอีเมลไปยังลูกค้า 100 คน และคาดว่ามีโอกาสที่ลูกค้าจะตอบกลับ 10% (ใช้ Binomial Distribution)

import numpy as np
import matplotlib.pyplot as plt

# จำนวนลูกค้าเป้าหมาย
n_customers = 100  

# ความน่าจะเป็นที่ลูกค้าจะตอบกลับ
p_response = 0.1  

# สร้างข้อมูลจำลองจาก Binomial Distribution
n_simulations = 1000  # จำนวนการทดลอง

rng = np.random.default_rng(seed=42)
responses = rng.binomial(n_customers, p_response, n_simulations)

# แสดงข้อมูลตัวอย่าง
print("ตัวอย่างจำนวนลูกค้าที่ตอบกลับต่อแคมเปญ:", responses[:10])

# การสร้าง Histogram
plt.hist(responses, bins=range(min(responses), max(responses) + 2), align='left', rwidth=0.8, color='skyblue', edgecolor='black')
plt.title("Customer Responses to Marketing Campaign (Binomial Distribution)")
plt.xlabel("Number of Responses")
plt.ylabel("Frequency")
plt.show()

ผลลัพธ์: ตัวอย่างจำนวนลูกค้าที่ตอบกลับต่อแคมเปญ: [12 9 13 11 6 16 12 12 7 9]

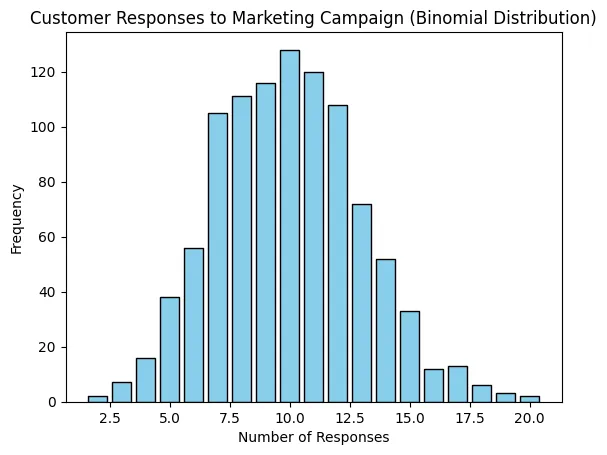
ซึ่งผลลัพธ์จาก Binomial Distribution (ตอบกลับแคมเปญ) นี้ ช่วยวิเคราะห์ประสิทธิภาพของแคมเปญ เช่น หากพบว่าค่าตอบกลับต่ำกว่าคาด อาจต้องปรับปรุงข้อความหรือวิธีการส่งแคมเปญ

การเลือก Distribution

การเลือก Discrete Distribution ที่เหมาะสมกับแต่ละ Use Case จำเป็นต้องพิจารณาลักษณะของข้อมูลและปัญหาที่ต้องการวิเคราะห์ ซึ่งสามารถแบ่งออกเป็นเกณฑ์ที่ช่วยในการตัดสินใจได้ดังนี้

1. ลักษณะของเหตุการณ์

• Binomial Distribution: ใช้เมื่อเหตุการณ์มีผลลัพธ์ 2 แบบชัดเจน เช่น สำเร็จ/ล้มเหลว, ใช่/ไม่ใช่ หรือ หัว/ก้อย
  • Use Case:
    • การวิเคราะห์อัตราการตอบกลับอีเมล (ตอบ/ไม่ตอบ)
    • การทดสอบว่าผลิตภัณฑ์ใหม่จะได้รับความนิยมในกลุ่มตัวอย่างหรือไม่
• Poisson Distribution: ใช้เมื่อเหตุการณ์เกี่ยวข้องกับ การนับจำนวนครั้ง ที่เกิดขึ้นในช่วงเวลาหรือพื้นที่ เช่น จำนวนอีเมลที่ได้รับในหนึ่งชั่วโมง หรือจำนวนลูกค้าที่มาถึงร้าน
  • Use Case:
    • การคาดการณ์จำนวนลูกค้าที่เข้ามาในร้านต่อชั่วโมง
    • การวิเคราะห์จำนวนการโทรเข้าสายด่วนในช่วงเวลาที่กำหนด

2. ลักษณะของตัวแปรที่ต้องวิเคราะห์

• Geometric Distribution: ใช้เมื่อสนใจ จำนวนครั้งที่ต้องใช้จนกว่าจะเกิดความสำเร็จครั้งแรก เช่น จำนวนครั้งที่ต้องทอยลูกเต๋าเพื่อออกหน้า 6
  • Use Case:
    • การคาดการณ์จำนวนการโทรติดต่อลูกค้าเพื่อปิดการขายครั้งแรก
    • การวิเคราะห์จำนวนครั้งที่ต้องทดสอบระบบก่อนที่จะผ่านการทดสอบ
• Negative Binomial Distribution: ใช้ในกรณีที่ต้องการนับจำนวนครั้งที่ต้องใช้จนกว่าจะเกิด จำนวนความสำเร็จที่กำหนดไว้ เช่น จำนวนครั้งที่ต้องยิงโฆษณาจนได้ยอดขาย 10 ชิ้น
  • Use Case:
    • การวิเคราะห์แคมเปญการตลาดที่ต้องการจำนวนลูกค้าเป้าหมายขั้นต่ำ
    • การทดสอบคุณภาพสินค้าเพื่อหาค่าความสำเร็จตามจำนวนครั้งที่กำหนด

3. ลักษณะของข้อมูลในบริบทที่กำหนด

• Hypergeometric Distribution: ใช้ในกรณีที่สุ่มเลือกจากประชากรที่มีขนาดจำกัด (ไม่มีการคืนค่าหลังเลือก) เช่น การสุ่มเลือกสินค้าในคลังเพื่อตรวจสอบคุณภาพ
  • Use Case:
    • การตรวจสอบคุณภาพสินค้าในคลังที่สุ่มเลือกจำนวนหนึ่งจากล็อต
    • การวิเคราะห์การสุ่มเลือกไพ่หรือการสุ่มเลือกตัวอย่างจากประชากรจำกัด

ดังนั้น หลักการเลือก Distribution เรามักจะพิจารณาจาก

1. พิจารณาลักษณะของเหตุการณ์ที่ต้องวิเคราะห์ (2 ทางเลือก, การนับ, หรือจำนวนครั้ง)
2. เลือก Distribution ที่เหมาะสมตามลักษณะของตัวแปรและบริบท
3. ทดสอบด้วยการสร้างข้อมูลจำลองใน Python เพื่อดูการกระจายตัวและความเหมาะสม

ตารางสรุป โดยประมาณ

Distribution	Key Characteristics	Example Use Case
Binomial	เหตุการณ์ 2 แบบ (สำเร็จ/ล้มเหลว)	อัตราการตอบกลับอีเมล หรืออัตราความสำเร็จในแคมเปญโฆษณา
Poisson	การนับจำนวนเหตุการณ์ในช่วงเวลา/พื้นที่	จำนวนลูกค้าที่เข้าร้านต่อชั่วโมง หรือจำนวนการโทรเข้าสายด่วน
Geometric	จำนวนครั้งที่ต้องใช้ก่อนความสำเร็จครั้งแรก	จำนวนครั้งที่ต้องโทรหาลูกค้าก่อนปิดการขายครั้งแรก
Negative Binomial	จำนวนครั้งที่ต้องใช้จนกว่าจะได้จำนวนสำเร็จที่กำหนด	การยิงโฆษณาจนได้ยอดขายครบ 10 ชิ้น
Hypergeometric	การสุ่มเลือกจากประชากรแบบจำกัด (ไม่มีคืนค่า)	การตรวจสอบคุณภาพสินค้าในล็อตหรือสุ่มเลือกทีมงานจากกลุ่มที่มีความเชี่ยวชาญเฉพาะ

Continuous Distributions

Continuous Distributions คือการแจกแจงความน่าจะเป็นของตัวแปรสุ่มที่สามารถรับค่าใด ๆ ก็ได้ในช่วงของตัวเลขที่ต่อเนื่อง เช่น น้ำหนัก ความสูง อุณหภูมิ หรือเวลา การแจกแจงเหล่านี้เหมาะกับข้อมูลที่ไม่สามารถนับได้ทีละตัว (infinite values within a range) แต่สามารถวัดได้

ตัวอย่างของ Continuous Distributions ที่นิยมใช้ ได้แก่

1. Normal Distribution: ใช้ในข้อมูลที่มีการกระจายตัวตามธรรมชาติ เช่น คะแนนสอบ หรือความสูงของคนในประชากร
2. Exponential Distribution: ใช้ในการวิเคราะห์เวลาระหว่างเหตุการณ์ เช่น เวลารอคิว
3. Uniform Distribution: ใช้เมื่อค่าความน่าจะเป็นกระจายตัวอย่างเท่าเทียมกันในทุกช่วง

เราจะยกตัวอย่างใน Python โดยใช้ Normal Distribution โดยใช้ library numpy เพื่อสร้างข้อมูลจำลองที่กระจายตัวตามลักษณะของระฆังคว่ำ

import numpy as np
import matplotlib.pyplot as plt

# ตั้งค่าพารามิเตอร์ของ Normal Distribution
mean = 50      # ค่าเฉลี่ย
std_dev = 10    # ส่วนเบี่ยงเบนมาตรฐาน
n_samples = 1000  # จำนวนข้อมูลจำลอง

# สร้างข้อมูลจำลองจาก Normal Distribution
rng = np.random.default_rng(seed=42)
data = rng.normal(mean, std_dev, n_samples)

# ดูตัวอย่างข้อมูล
print("ตัวอย่างข้อมูล:", data[:10])

# การสร้าง Histogram
plt.hist(data, bins=30, color='skyblue', edgecolor='black', density=True)
plt.title("Histogram of Normal Distribution")
plt.xlabel("Value")
plt.ylabel("Density")
plt.axvline(mean, color='red', linestyle='dashed', linewidth=1, label=f"Mean = {mean}")
plt.legend()
plt.show()

ผลลัพธ์: ตัวอย่างข้อมูล: [53.0471708 39.60015894 57.50451196 59.40564716 30.48964811 36.97820493 51.27840403 46.83757408 49.83198842 41.46956072]

ตัวอย่างที่ 1: การวิเคราะห์เวลารอของลูกค้า

สมมติว่าเวลารอเฉลี่ยของลูกค้าในการเข้ารับบริการคือ 5 นาที และเราต้องการดูว่าการกระจายเวลารอของลูกค้าเป็นอย่างไร (Exponential Distribution)

import numpy as np
import matplotlib.pyplot as plt

# ค่าเฉลี่ยเวลารอ (lambda = 1/mean)
mean_wait_time = 5  # นาที
n_customers = 1000  # จำนวนลูกค้า

# สร้างข้อมูลจำลองจาก Exponential Distribution
data = np.random.exponential(mean_wait_time, n_customers)

# แสดงข้อมูลตัวอย่าง
print("ตัวอย่างเวลารอ:", data[:10])

# การสร้าง Histogram
plt.hist(data, bins=30, color='lightgreen', edgecolor='black', density=True)
plt.title("Histogram of Exponential Distribution")
plt.xlabel("Wait Time (minutes)")
plt.ylabel("Density")
plt.axvline(mean_wait_time, color='red', linestyle='dashed', linewidth=1, label=f"Mean = {mean_wait_time} min")
plt.legend()
plt.show()

ผลลัพธ์ ตัวอย่างเวลารอ: [7.52633664 5.79328404 8.85195416 7.56030339 6.878984 2.41808837 1.45288955 3.66071087 9.20080408 2.79687259]

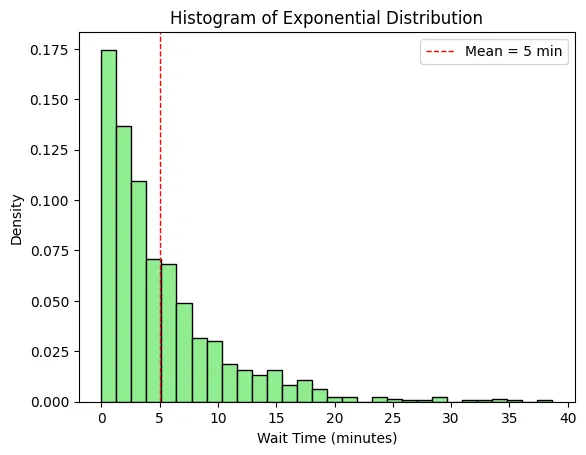
ตัวอย่างที่ 2: คะแนนสอบนักเรียน

ในกรณีของคะแนนสอบนักเรียนในห้องเรียน:

• คะแนนมักกระจายตัวรอบค่าเฉลี่ย (เช่น คะแนนส่วนใหญ่อยู่ในช่วงที่ใกล้เคียงค่าเฉลี่ย)
• มีนักเรียนบางคนที่ได้คะแนนสูงหรือต่ำผิดปกติ แต่จำนวนเหล่านี้น้อยมาก
• การกระจายตัวของคะแนนมักมีลักษณะเป็นรูประฆังคว่ำ (Bell Curve)

สมมติฐาน

• คะแนนเฉลี่ยของนักเรียนในห้องคือ 70 คะแนน
• ส่วนเบี่ยงเบนมาตรฐาน (Standard Deviation) คือ 10 คะแนน (แสดงถึงความกระจายตัวของคะแนน)
• คะแนนสอบอยู่ในช่วง 0–100

ด้วย python code นี้

import numpy as np
import matplotlib.pyplot as plt

# ค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของคะแนนสอบ
mean = 70
std_dev = 10

# สร้างข้อมูลจำลอง
data = np.random.normal(mean, std_dev, 1000)

# Histogram
plt.hist(data, bins=30, color='blue', edgecolor='black', density=True)
plt.title("Histogram of Normal Distribution (Exam Scores)")
plt.xlabel("Scores")
plt.ylabel("Density")
plt.axvline(mean, color='red', linestyle='dashed', linewidth=1, label=f"Mean = {mean}")
plt.legend()
plt.show()

ผลลัพธ์: ตัวอย่างคะแนนสอบ: [71.70949858 60.78474038 63.83927356 74.00573251 59.51486734 76.01212841 68.7673164 72.88833069 71.27839482 71.89537245]

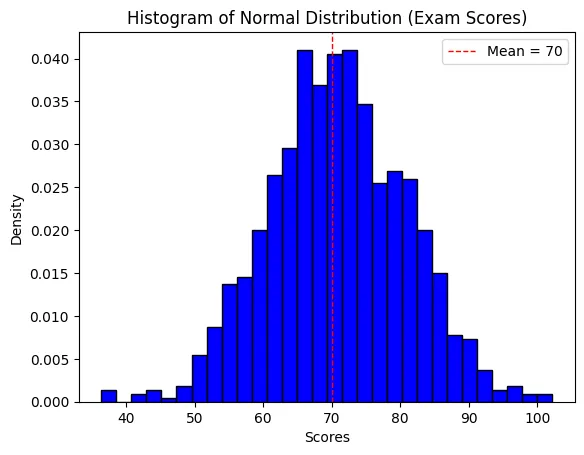
ก็จะสามารถใช้ตรวจสอบได้ว่าการกระจายตัวของคะแนน ที่เป็นลักษณะ Normal Distribution ควรกระจายตัวลักษณะใดได้

การเลือก Distribution

การเลือก Continuous Distributions ที่เหมาะสมสำหรับแต่ละ Use Case ขึ้นอยู่กับลักษณะของข้อมูลและลักษณะของปัญหาที่ต้องการวิเคราะห์ คุณสามารถพิจารณาจากเกณฑ์เหล่านี้:

1. ลักษณะของการกระจายตัวของข้อมูล

• Normal Distribution: ใช้เมื่อข้อมูลมีลักษณะสมมาตร (symmetrical) และกระจายตัวรอบค่าเฉลี่ย เหมาะสำหรับข้อมูลที่พบได้ทั่วไป เช่น คะแนนสอบ, ความสูง, น้ำหนัก
  • Use Case:
    • การวิเคราะห์ข้อมูลที่เกี่ยวกับค่าเฉลี่ยและความเบี่ยงเบน เช่น การวิเคราะห์ประสิทธิภาพพนักงาน
    • การสร้างโมเดลทางสถิติ เช่น Linear Regression
• Exponential Distribution: ใช้เมื่อสนใจเวลาหรือระยะเวลาระหว่างเหตุการณ์ เช่น เวลารอคิว หรือเวลาที่เซิร์ฟเวอร์ล่ม การกระจายตัวจะมีค่าเริ่มต้นที่ 0 และลดลงแบบเอ็กซ์โพเนนเชียล
  • Use Case:
    • การวิเคราะห์เวลารอของลูกค้าในร้าน
    • การคาดการณ์อายุการใช้งานของอุปกรณ์
• Uniform Distribution: ใช้เมื่อค่าความน่าจะเป็นกระจายตัวอย่างสม่ำเสมอ (ทุกค่าในช่วงที่กำหนดมีโอกาสเกิดเท่ากัน)
  • Use Case:
    • การสุ่มเลขในช่วงตัวเลข เช่น การสุ่มตัวอย่างลูกค้าเพื่อทำแบบสำรวจ
    • การจำลองเหตุการณ์ที่ไม่มี bias เช่น การสุ่มหมุนรูเล็ต

2. ลักษณะของปัญหา

• ถ้าข้อมูลมีค่าเฉลี่ยที่เป็นตัวแทนหลัก:
  • ใช้ Normal Distribution หากข้อมูลกระจายตัวสมมาตร
  • ใช้ Exponential Distribution หากสนใจเวลาระหว่างเหตุการณ์
• ถ้าข้อมูลทุกค่ามีโอกาสเกิดเท่าๆ กัน: ใช้ Uniform Distribution
• ถ้าข้อมูลมีความสุดโต่งหรือลำเอียง: ใช้ Distribution แบบอื่น เช่น Log-Normal หรือ Gamma

ตารางสรุปโดยประมาณ

Distribution	Key Characteristics	Example Use Case
Normal	สมมาตรรอบค่าเฉลี่ย	การวิเคราะห์คะแนนสอบ หรือข้อมูลสุขภาพ
Exponential	เวลาระหว่างเหตุการณ์, ค่าเริ่มต้นที่ 0	การวิเคราะห์เวลารอคิว หรืออายุการใช้งานอุปกรณ์
Uniform	ความน่าจะเป็นกระจายตัวเท่ากันในทุกช่วง	การสุ่มเลือกตัวเลขสำหรับการจำลองหรือการทดลอง
Log-Normal	ข้อมูลที่มีการกระจายแบบไม่สมมาตร, ค่ามากสุดโต่ง	การวิเคราะห์ราคาสินทรัพย์ทางการเงิน
Gamma	เวลารอที่มีหลายเหตุการณ์รวมกัน	การวิเคราะห์เวลาที่ต้องใช้สำหรับกระบวนการหลายขั้นตอน

การตรวจสอบ Distribution

การตรวจสอบ Distribution คือกระบวนการวิเคราะห์เพื่อทำความเข้าใจรูปแบบการกระจายตัวของข้อมูล (Data Distribution) โดยดูว่าข้อมูลมีการกระจายตัวอย่างไร เช่น สมมาตร, เอียงไปด้านใดด้านหนึ่ง, หรือมี Outliers หรือไม่ การตรวจสอบนี้สำคัญสำหรับการเลือกวิธีการวิเคราะห์ข้อมูลที่เหมาะสม เช่น การเลือกโมเดลทางสถิติหรือ Machine Learning Algorithm ที่เหมาะสมกับลักษณะของข้อมูล

ขั้นตอนการตรวจสอบ Distribution

1. วิเคราะห์ภาพรวมของข้อมูล:
   • ใช้สถิติพื้นฐาน เช่น ค่าเฉลี่ย (Mean), มัธยฐาน (Median), และส่วนเบี่ยงเบนมาตรฐาน (Standard Deviation)
   • ดูค่าความเอียง (Skewness) และความแหลม (Kurtosis)
2. การวาดกราฟ Distribution:
   • ใช้ Histogram, KDE (Kernel Density Estimation), หรือ Boxplot เพื่อดูการกระจายตัวของข้อมูล
3. เปรียบเทียบกับ Distribution ที่รู้จัก:
   • เช่น ตรวจสอบว่าข้อมูลใกล้เคียงกับ Normal Distribution หรือไม่