รู้จักกับสถิติ

สามารถดู video ของหัวข้อนี้ก่อนได้ ดู video

การวิเคราะห์ทางสถิติคืออะไร?

การวิเคราะห์ทางสถิติ คือ กระบวนการใช้เทคนิคและวิธีการทางสถิติเพื่อรวบรวม สรุป วิเคราะห์ และแปลผลข้อมูลที่ได้จากการเก็บรวบรวมในรูปแบบต่าง ๆ

การเก็บรวบรวมข้อมูล: นี่เป็นขั้นตอนแรก ซึ่งประกอบด้วยการรวบรวมข้อมูลที่เกี่ยวข้องกับปัญหาหรือประเด็นที่กำลังศึกษา ข้อมูลอาจเป็น ข้อมูลปฐมภูมิ ที่เก็บโดยตรงเพื่อการศึกษานั้น ๆ หรือ ข้อมูลทุติยภูมิ ที่ได้จากแหล่งข้อมูลที่มีอยู่แล้ว
การจัดระเบียบข้อมูล: ข้อมูลที่เก็บรวบรวมมาอาจยังอยู่ในรูปแบบดิบและจำเป็นต้องจัดระเบียบก่อนการวิเคราะห์ ซึ่งรวมถึง การจัดจำแนก (classifying) ข้อมูลออกเป็นกลุ่มตามลักษณะร่วม และ การจัดทำตาราง (tabulating) ข้อมูลในรูปแบบแถวและคอลัมน์เพื่อการนำเสนอและทำความเข้าใจที่ง่ายขึ้น
การวิเคราะห์ข้อมูล: ขั้นตอนนี้เกี่ยวข้องกับการใช้วิธีการและมาตรการทางสถิติต่าง ๆ เพื่อทำความเข้าใจกับคุณลักษณะของข้อมูลและสรุปผลที่มีความหมาย ประเด็นสำคัญของการวิเคราะห์ข้อมูลประกอบด้วย:
- การคำนวณการวัดแนวโน้มเข้าสู่ศูนย์กลาง (Measures of central tendency): ซึ่งหมายถึงการหาค่าที่แสดงถึงค่ากลางหรือค่าที่เป็นตัวแทนของข้อมูล เช่น ค่าเฉลี่ย (Mean) มัธยฐาน (Median) และฐานนิยม (Mode)
- การกำหนดการวัดการกระจาย (Measures of dispersion): เป็นการหาค่าที่แสดงถึงความกระจายตัวหรือความแปรปรวนของข้อมูล เช่น พิสัย (Range) ส่วนเบี่ยงเบนเฉลี่ย (Mean deviation) ส่วนเบี่ยงเบนมาตรฐาน (Standard deviation) และความแปรปรวน (Variance)
- การระบุรูปแบบและความสัมพันธ์: รวมถึงการวิเคราะห์ข้อมูลอนุกรมเวลา (Time series) เพื่อทำความเข้าใจแนวโน้มและคาดการณ์พฤติกรรมในอนาคต และการศึกษาความสัมพันธ์ระหว่างตัวแปรโดยใช้การวิเคราะห์สหสัมพันธ์ (Correlation) และการวิเคราะห์ถดถอย (Regression analysis)
การตีความและการนำเสนอผลลัพธ์: ขั้นตอนสุดท้ายคือการตีความผลลัพธ์จากการวิเคราะห์และนำเสนอในรูปแบบที่ชัดเจนและเข้าใจง่าย โดยใช้ตาราง แผนภาพ และกราฟ

สถิติเป็นศาสตร์ที่เกี่ยวข้องกับการศึกษา การวิเคราะห์ และการตีความข้อมูล เพื่อช่วยให้เราเข้าใจและนำข้อมูลไปใช้ในการตัดสินใจหรือคาดการณ์ โดยทั่วไปสถิติสามารถแบ่งออกเป็นสองแขนงหลัก ได้แก่ Descriptive Statistics ซึ่งเน้นการสรุปและนำเสนอข้อมูลในรูปแบบที่เข้าใจง่าย เพื่อแสดงภาพรวมของข้อมูล และ Inferential Statistics ที่มุ่งเน้นการใช้ข้อมูลตัวอย่างในการอนุมานหรือคาดการณ์ผลลัพธ์ในระดับประชากร ทั้งสองแขนงนี้ทำงานร่วมกันเพื่อช่วยให้เราสามารถวิเคราะห์ข้อมูลได้อย่างมีประสิทธิภาพและลึกซึ้ง

Descriptive Statistics คือศาสตร์ที่เกี่ยวข้องกับการเก็บรวบรวมข้อมูล การสรุปผล และการนำเสนอข้อมูลในรูปแบบที่เข้าใจง่าย เช่น การหาค่าเฉลี่ย (Mean), มัธยฐาน (Median), ฐานนิยม (Mode), การวัดการกระจายตัว เช่น ส่วนเบี่ยงเบนมาตรฐาน (Standard Deviation) หรือช่วงข้อมูล (Range) รวมถึงการแสดงผลด้วยกราฟต่าง ๆ เช่น กราฟแท่ง (Bar Chart), ฮิสโทแกรม (Histogram) หรือไดอะแกรมวงกลม (Pie Chart) โดยเป้าหมายของ Descriptive Statistics คือการอธิบายข้อมูลให้เห็นภาพรวมและลักษณะสำคัญของข้อมูลชุดนั้น ๆ โดยไม่ทำการสรุปหรือคาดการณ์อะไรเพิ่มเติม
Inferential Statistics คือศาสตร์ที่ใช้ในการวิเคราะห์และตีความข้อมูลเพื่อทำการอนุมาน (Inference) หรือคาดการณ์ผลลัพธ์ในระดับประชากร (Population) โดยใช้ข้อมูลจากตัวอย่าง (Sample) การวิเคราะห์เชิงอนุมานจะใช้เทคนิคทางสถิติ เช่น การทดสอบสมมติฐาน (Hypothesis Testing), การวิเคราะห์ความสัมพันธ์ (Correlation), การวิเคราะห์ความแปรปรวน (ANOVA) หรือการสร้างโมเดลเชิงพยากรณ์ (Predictive Modeling) เป้าหมายหลักคือการสรุปผลและนำเสนอข้อมูลที่สามารถใช้ในการตัดสินใจหรือคาดการณ์ในสถานการณ์ที่ไม่สามารถเก็บข้อมูลทั้งหมดได้

เราจะเริ่มมาทำความรู้จักกับ Descriptive Statistics กันก่อน

Descriptive Statistics

Descriptive Statistics (สถิติเชิงพรรณนา) คือ สาขาหนึ่งของสถิติที่เกี่ยวข้องกับการสรุปและอธิบายลักษณะของข้อมูลที่รวบรวมมา โดยไม่มีการคาดการณ์หรืออ้างอิงถึงประชากร (population) ทั้งหมด แต่เน้นแค่ข้อมูลชุดที่มีอยู่ (sample) เพื่อทำให้ข้อมูลนั้นง่ายต่อการทำความเข้าใจและสื่อสารผลได้อย่างชัดเจน

ตัวอย่างของการใช้งาน Descriptive Statistics ได้แก่

การวัดแนวโน้มเข้าสู่ศูนย์กลางของข้อมูล (Measures of Central Tendency): เช่น ค่าเฉลี่ย (Mean), มัธยฐาน (Median), ฐานนิยม (Mode)
การวัดการกระจายตัวของข้อมูล (Measures of Dispersion): เช่น พิสัย (Range), ส่วนเบี่ยงเบนมาตรฐาน (Standard Deviation), ความแปรปรวน (Variance)
การแสดงข้อมูลในรูปแบบภาพ: เช่น ตารางความถี่ (Frequency Table), ฮิสโตแกรม (Histogram), แผนภูมิแท่ง (Bar Chart)

จุดประสงค์หลักของ Descriptive Statistics

สรุปข้อมูลให้อยู่ในรูปแบบที่เข้าใจง่าย เช่น การใช้ตัวเลขเพียงไม่กี่ตัวหรือตาราง/กราฟ
ใช้เพื่อเปรียบเทียบข้อมูลจากกลุ่มตัวอย่างหรือจากแหล่งข้อมูลที่แตกต่างกัน

ตัวอย่างเช่น

ถ้าคุณมีคะแนนสอบของนักเรียน 30 คน คุณอาจใช้ค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานเพื่อบอกลักษณะทั่วไปของคะแนนนั้น เช่น คะแนนเฉลี่ยของนักเรียนคือ 75 และส่วนเบี่ยงเบนมาตรฐานคือ 10 ซึ่งแปลว่าคะแนนส่วนใหญ่อยู่ในช่วง 65-85

Descriptive Statistics ช่วยให้เราเข้าใจข้อมูลในภาพรวมก่อนที่จะก้าวไปสู่การวิเคราะห์ขั้นสูง เช่น Inferential Statistics ที่จะใช้ในการทำนายหรือสรุปผลสำหรับประชากรทั้งกลุ่ม

เราจะมาทำความรู้จักแต่ละตัวละครผ่าน python code กัน

Mean (ค่าเฉลี่ย)

ค่าเฉลี่ยคือผลรวมของข้อมูลทั้งหมดหารด้วยจำนวนข้อมูล ใช้เพื่อแสดงค่ากลางของข้อมูลชุดนั้น

สูตร

\text{Mean} = \frac{\text{Sum of all data points}}{\text{Number of data points}}

ตัวอย่าง Python

ใช้ numpy.mean() ในการหาค่าเฉลี่ย

import numpy as np

data = [10, 20, 30, 40, 50]
mean = np.mean(data)
print("Mean:", mean) # 30

โดย Mean นั้น เหมาะสำหรับการวิเคราะห์ข้อมูลที่มีการกระจายตัวสมดุลและไม่มี Outlier ที่รบกวนค่าเฉลี่ยมากเกินไป

Use Case ที่เหมาะสมเช่น

วิเคราะห์รายได้เฉลี่ยของพนักงาน: เพื่อวางแผนนโยบายหรือจัดการงบประมาณ
คำนวณคะแนนเฉลี่ยในชั้นเรียน: เพื่อดูภาพรวมของผลการเรียน
ประเมินค่าเฉลี่ยของอุณหภูมิ: ในการวิจัยการเปลี่ยนแปลงของสภาพอากาศในแต่ละวัน

Median (ค่ามัธยฐาน)

ค่ามัธยฐานคือค่ากลางของข้อมูลเมื่อเรียงลำดับจากน้อยไปมาก หากจำนวนข้อมูลเป็นเลขคู่ จะใช้ค่าเฉลี่ยของสองตัวกลาง

ตัวอย่าง Python:

ใช้ numpy.median() ในการหา Median

import numpy as np

data = [10, 20, 30, 40, 50]
median = np.median(data)
print("Median:", median) # 30.0

# **กรณีข้อมูลเลขคู่**
data_even = [10, 20, 30, 40]
median_even = np.median(data_even)
print("Median (Even):", median_even) # 25.0

โดย Median เหมาะสำหรับข้อมูลที่มี Outlier สูง เช่น ค่าที่กระโดดมากเกินไปจะไม่ส่งผลต่อมัธยฐาน

Use Case ที่เหมาะสม

วิเคราะห์ราคากลางของบ้านในตลาดอสังหาริมทรัพย์: เพื่อสะท้อนราคาที่แท้จริงในพื้นที่โดยไม่ถูกราคาบ้านหรูเกินไปดึงค่า
ประเมินรายได้ของประชากร: เพื่อดูความเหลื่อมล้ำโดยลดอิทธิพลจากรายได้สูงมาก
คำนวณเวลามัธยฐานในการเดินทาง: เพื่อดูเวลาปกติในการเดินทางของคนในพื้นที่

Mode (ฐานนิยม)

ฐานนิยมคือค่าที่เกิดซ้ำบ่อยที่สุดในชุดข้อมูล หากมีค่าหลายค่าที่ซ้ำเท่ากัน จะคืนค่าทั้งหมด

ตัวอย่าง Python:

ใช้ scipy.stats.mode() ในการคำนวณหา mode

from scipy import stats

data = [10, 20, 20, 30, 30, 30, 40]
mode = stats.mode(data)
print("Mode:", mode.mode, "Frequency:", mode.count)
# Mode: 30 Frequency: 3

Scipy (https://scipy.org/) เป็น library ใน Python ที่ออกแบบมาเพื่อช่วยในการคำนวณเชิงตัวเลขและการวิเคราะห์ข้อมูลขั้นสูง โดย Scipy ขยายความสามารถของ NumPy ด้วย function เฉพาะทาง เช่น การคำนวณทางสถิติ การแก้สมการเชิงเส้นและไม่เชิงเส้น, Fourier Analysis, Signal Processing, Integration & Differentiation

Scipy มี module ที่ออกแบบมาเพื่องานเฉพาะ เช่น

scipy.stats สำหรับการวิเคราะห์ทางสถิติ
scipy.linalg สำหรับการคำนวณพีชคณิตเชิงเส้น
scipy.optimize สำหรับการหา Optimization และ Root Finding
รวมถึง scipy.signal และ scipy.spatial สำหรับการประมวลผลสัญญาณและการจัดการข้อมูลในเชิงเรขาคณิต

โดย Mode เหมาะสำหรับข้อมูลที่ต้องการหาค่าที่เกิดซ้ำบ่อยที่สุดในชุดข้อมูล

Use Case ที่เหมาะสม

วิเคราะห์สินค้าขายดีในร้านค้า: เพื่อวางแผนสต็อกสินค้า
คำนวณคะแนนที่พบบ่อยที่สุดในข้อสอบ: เพื่อดูว่าข้อใดทำให้นักเรียนส่วนใหญ่ทำผิดหรือถูก
วิเคราะห์ชื่อยอดนิยมของเด็กแรกเกิดในปีนั้น: เพื่อดูแนวโน้มการตั้งชื่อ

Graphs ที่เหมาะสมสำหรับ Mean, Median, และ Mode

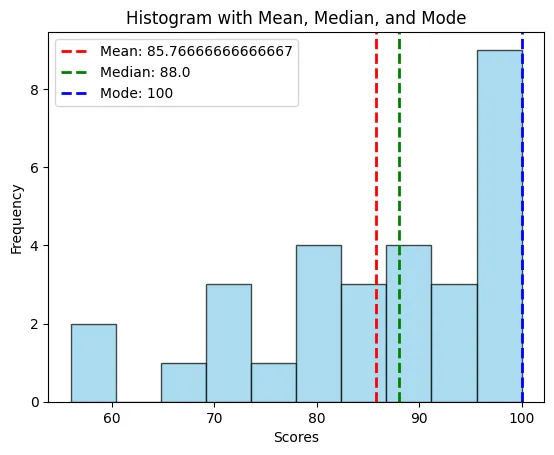
1. Histogram (พร้อม Mean, Median, Mode)

Histogram เหมาะสำหรับแสดงการกระจายตัวของข้อมูล พร้อมไฮไลต์จุดที่เป็น Mean, Median และ Mode เพื่อเปรียบเทียบในบริบทเดียวกัน

ตัวอย่างข้อมูล: สมมติข้อมูลคะแนนสอบของนักเรียน 30 คน

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# ตัวอย่างข้อมูล
data = [56, 60, 65, 70, 72, 72, 75, 78, 80, 82, 82, 83, 85, 85, 88, 88, 88, 90, 92, 95, 95, 96, 98, 98, 100, 100, 100, 100, 100, 100]

# คำนวณ Mean, Median, Mode
mean = np.mean(data)
median = np.median(data)
mode = stats.mode(data).mode

# สร้างกราฟ Histogram
plt.hist(data, bins=10, alpha=0.7, color='skyblue', edgecolor='black')
plt.axvline(mean, color='red', linestyle='dashed', linewidth=2, label=f'Mean: {mean}')
plt.axvline(median, color='green', linestyle='dashed', linewidth=2, label=f'Median: {median}')
plt.axvline(mode, color='blue', linestyle='dashed', linewidth=2, label=f'Mode: {mode}')

# ตั้งค่าและแสดงผล
plt.title('Histogram with Mean, Median, and Mode')
plt.xlabel('Scores')
plt.ylabel('Frequency')
plt.legend()
plt.show()

Output ที่ได้:

กราฟ Histogram ที่มีเส้นแนวตั้งแสดงตำแหน่งของ Mean (แดง), Median (เขียว), และ Mode (น้ำเงิน)

2. Boxplot (สำหรับ Median)

Boxplot เหมาะสำหรับการแสดง Median และกระจายตัวของข้อมูล รวมถึง Outlier

ตัวอย่างข้อมูล: สมมติข้อมูลคะแนนสอบของนักเรียน 30 คน (ชุดเดียวกันกับอันแรก)

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# ตัวอย่างข้อมูล
data = [56, 60, 65, 70, 72, 72, 75, 78, 80, 82, 82, 83, 85, 85, 88, 88, 88, 90, 92, 95, 95, 96, 98, 98, 100, 100, 100, 100, 100, 100]

median = np.median(data)

# สร้าง Boxplot
plt.boxplot(data, vert=False, patch_artist=True, boxprops=dict(facecolor='lightblue', color='blue'))
plt.axvline(median, color='green', linestyle='dashed', linewidth=2, label=f'Median: {median}')
plt.title('Boxplot with Median')
plt.xlabel('Scores')
plt.legend()
plt.show()

Output ที่ได้:

กราฟ Boxplot แสดงค่ามัธยฐาน (Median) ด้วยเส้นสีเขียว

3. Bar Chart (สำหรับ Mode)

Bar Chart เหมาะสำหรับแสดงค่าที่เกิดซ้ำบ่อยที่สุด (Mode)

ตัวอย่างข้อมูล:

from collections import Counter
import matplotlib.pyplot as plt
from scipy import stats

# ตัวอย่างข้อมูล
data = [56, 60, 65, 70, 72, 72, 75, 78, 80, 82, 82, 83, 85, 85, 88, 88, 88, 90, 92, 95, 95, 96, 98, 98, 100, 100, 100, 100, 100, 100]
mode = stats.mode(data).mode

# นับความถี่ของข้อมูล
data_counts = Counter(data)
most_common = data_counts.most_common()

# เตรียมข้อมูลสำหรับ Bar Chart
values, frequencies = zip(*most_common)

# สร้างกราฟ Bar Chart
plt.bar(values, frequencies, color='lightcoral', edgecolor='black')
plt.title('Bar Chart for Mode')
plt.xlabel('Scores')
plt.ylabel('Frequency')
plt.axvline(mode, color='blue', linestyle='dashed', linewidth=2, label=f'Mode: {mode}')
plt.legend()
plt.show()

Output ที่ได้:

กราฟ Bar Chart แสดงความถี่ของข้อมูลพร้อมไฮไลต์ Mode

Note

Histogram: เหมาะสำหรับแสดงการกระจายตัวและเปรียบเทียบ Mean, Median, Mode
Boxplot: แสดง Median และ Outliers
Bar Chart: แสดงค่าที่เกิดซ้ำบ่อยที่สุด (Mode)

Standard Deviation (ส่วนเบี่ยงเบนมาตรฐาน)

Standard Deviation (SD) คือค่าที่บ่งบอกถึงการกระจายตัวของข้อมูลจากค่าเฉลี่ย (Mean) โดย

ค่ายิ่งน้อยแสดงว่าข้อมูลกระจุกตัวใกล้ค่าเฉลี่ยมาก
หากค่ายิ่งสูงแสดงว่าข้อมูลมีการกระจายตัวห่างจากค่าเฉลี่ยมาก

สูตรคำนวณ:

\text{SD} = \sqrt{\frac{\sum (x_i - \mu)^2}{N}}

$x_i$ : ค่าแต่ละตัวในข้อมูล
$\mu$ : ค่าเฉลี่ย (Mean)
$N$ : จำนวนข้อมูลทั้งหมด

ตัวอย่างใน Python

สมมติข้อมูล: คะแนนสอบของนักเรียนในชั้นเรียน

import numpy as np

# ตัวอย่างข้อมูล
data = [60, 62, 65, 67, 70, 72, 75, 78, 80, 82]

# คำนวณค่า Standard Deviation
std_dev = np.std(data)
print("Standard Deviation:", std_dev)

Output:

Standard Deviation: 6.565059022609256

คำอธิบายเพิ่มเติม

Standard Deviation = 6.57: แสดงว่าคะแนนส่วนใหญ่กระจายตัวอยู่ในช่วง ±6.57 จากค่าเฉลี่ยของชุดข้อมูลนี้
ข้อมูลที่กระจายตัวมาก (SD สูง): มีความแตกต่างของข้อมูลสูง เช่น คะแนนมีตั้งแต่ 0 ถึง 100
ข้อมูลที่กระจายตัวน้อย (SD ต่ำ): ข้อมูลจะกระจุกตัวใกล้ค่าเฉลี่ย เช่น คะแนนมีแค่ 60–65

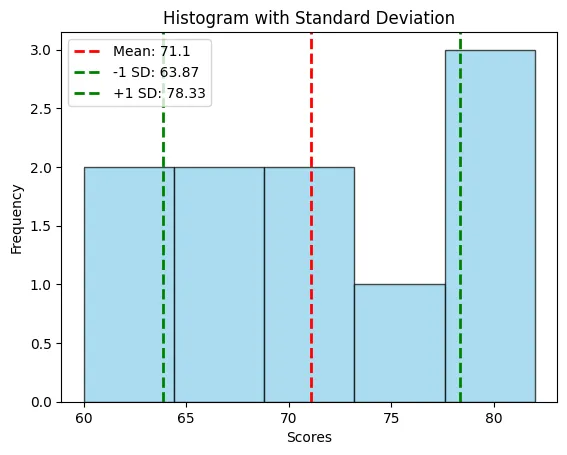
กราฟแสดง Standard Deviation

สามารถใช้กราฟ Histogram เพื่อแสดงการกระจายตัว พร้อมไฮไลต์ช่วงค่า ±1 SD จาก Mean:

import matplotlib.pyplot as plt

# คำนวณค่า Mean
mean = np.mean(data)

# สร้างกราฟ Histogram
plt.hist(data, bins=5, color='skyblue', edgecolor='black', alpha=0.7)
plt.axvline(mean, color='red', linestyle='dashed', linewidth=2, label=f'Mean: {mean}')
plt.axvline(mean - std_dev, color='green', linestyle='dashed', linewidth=2, label=f'-1 SD: {mean - std_dev:.2f}')
plt.axvline(mean + std_dev, color='green', linestyle='dashed', linewidth=2, label=f'+1 SD: {mean + std_dev:.2f}')

# ตั้งค่าและแสดงผล
plt.title('Histogram with Standard Deviation')
plt.xlabel('Scores')
plt.ylabel('Frequency')
plt.legend()
plt.show()

กราฟ Output:

เส้นสีแดงแสดงค่าเฉลี่ย (Mean)
เส้นสีเขียวสองเส้นแสดงช่วง ±1 Standard Deviation (SD) จากค่าเฉลี่ย

Variance (ความแปรปรวน)

Variance คือค่าที่แสดงถึงการกระจายตัวของข้อมูลในชุดข้อมูล โดยเป็นการวัดระยะห่างเฉลี่ยของข้อมูลจากค่าเฉลี่ย (Mean) ในรูปแบบยกกำลังสอง ค่า Variance ช่วยให้เข้าใจว่าข้อมูลกระจายตัวมากน้อยแค่ไหน แต่มีหน่วยเป็นกำลังสองของข้อมูลต้นฉบับ

สูตรคำนวณ Variance:

\text{Variance} = \frac{\sum (x_i - \mu)^2}{N}

$x_i$ : ค่าแต่ละตัวในข้อมูล
$\mu$ : ค่าเฉลี่ย (Mean)
$N$ : จำนวนข้อมูลทั้งหมด

Variance เป็นค่าที่สัมพันธ์กับ Standard Deviation (SD) โดย

\text{SD} = \sqrt{\text{Variance}}

ตัวอย่างใน Python

สมมติข้อมูล: คะแนนสอบของนักเรียนในชั้นเรียน

import numpy as np

# ตัวอย่างข้อมูล
data = [60, 62, 65, 67, 70, 72, 75, 78, 80, 82]

# คำนวณค่า Variance
variance = np.var(data)
print("Variance:", variance)

Output:

Variance: 43.11

คำอธิบายผลลัพธ์

Variance = 43.11: แสดงว่าข้อมูลคะแนนสอบกระจายตัวโดยเฉลี่ยห่างจากค่าเฉลี่ยในระดับ 43.11 (ยกกำลังสอง)

Variance และ Standard Deviation (SD) มีหน้าที่คล้ายกันในการวัดการกระจายตัวของข้อมูล แต่ต่างกันที่หน่วยและการใช้งาน:

Variance แสดงการกระจายตัวในหน่วย "กำลังสอง" ของข้อมูลต้นฉบับ ซึ่งเหมาะสำหรับการคำนวณเชิงทฤษฎี เช่น การวิเคราะห์ทางสถิติหรือการสร้าง model
SD ถอดรากที่สองจาก Variance เพื่อแสดงการกระจายตัวในหน่วยเดียวกับข้อมูลต้นฉบับ ทำให้อ่านและตีความผลได้ง่ายกว่า เช่น ในการอธิบายว่า "ข้อมูลส่วนใหญ่เบี่ยงเบนจากค่าเฉลี่ยประมาณเท่าไร" จึงนิยมใช้ SD ในการสื่อสารเชิงปฏิบัติในชีวิตประจำวัน

การใช้งานจริงของ Variance

การวิเคราะห์ความเสี่ยง: ใช้คำนวณความแปรปรวนของผลตอบแทนในพอร์ตการลงทุน
การควบคุมคุณภาพ: ตรวจสอบการกระจายตัวของค่าจากมาตรฐาน
การประเมินความเสถียรของข้อมูล: เช่น การกระจายตัวของผลสอบ คะแนนกีฬา ฯลฯ

การวิเคราะห์ทางสถิติคืออะไร?​

Descriptive Statistics​

Mean (ค่าเฉลี่ย)​

Median (ค่ามัธยฐาน)​

Mode (ฐานนิยม)​

Graphs ที่เหมาะสมสำหรับ Mean, Median, และ Mode​

Standard Deviation (ส่วนเบี่ยงเบนมาตรฐาน)​

Variance (ความแปรปรวน)​

การวิเคราะห์ทางสถิติคืออะไร?

Descriptive Statistics

Mean (ค่าเฉลี่ย)

Median (ค่ามัธยฐาน)

Mode (ฐานนิยม)

Graphs ที่เหมาะสมสำหรับ Mean, Median, และ Mode

Standard Deviation (ส่วนเบี่ยงเบนมาตรฐาน)

Variance (ความแปรปรวน)