แนะนำ Complexity

สามารถดู video ของหัวข้อนี้ก่อนได้ ดู video

Complexity คืออะไร ?

อัลกอริทึม (Algorithm) คือ ขั้นตอนหรือกระบวนการในการแก้ปัญหาอย่างเป็นลำดับขั้นตอน โดยมีจุดเริ่มต้นและจุดสิ้นสุดที่ชัดเจน เมื่อปฏิบัติตามขั้นตอนอย่างถูกต้องแล้วจะได้ผลลัพธ์ที่ต้องการ

ความซับซ้อนของอัลกอริทึม (Algorithm Complexity) หมายถึง การวัดประสิทธิภาพของอัลกอริทึมว่ามีความซับซ้อนมากน้อยเพียงใด โดยพิจารณาจากปัจจัยต่างๆ เช่น

1. เวลาในการประมวลผล (Time Complexity) คือ ระยะเวลาที่ Algorithm ใช้ในการประมวลผลข้อมูลขนาดต่างๆ
2. พื้นที่หน่วยความจำ (Space Complexity) คือ ปริมาณหน่วยความจำที่ Algorithm ต้องใช้ในการประมวลผล

การวัดความซับซ้อนของอัลกอริทึมมักใช้ "Notation Big-O" ซึ่งเป็นการประมาณค่าความซับซ้อนในกรณีที่ข้อมูลนำเข้ามีขนาดใหญ่มาก ๆ เช่น

• O(1) หมายถึง ความซับซ้อนคงที่ (Constant Complexity) ไม่ว่าข้อมูลจะมีขนาดเท่าใดก็ใช้เวลาคงที่
• O(n) หมายถึง ความซับซ้อนเชิงเส้น (Linear Complexity) เวลาขึ้นกับขนาดของข้อมูลโดยตรง
• O(n^2) หมายถึง ความซับซ้อนกำลังสอง (Quadratic Complexity) เวลาเพิ่มขึ้นเป็นกำลังสองของขนาดข้อมูล
• O(log n) หมายถึง ความซับซ้อนแบบลอการิทึม (Logarithmic Complexity) ซึ่งมีประสิทธิภาพสูง

โดยทั่วไปแล้ว Algorithm ที่มีความซับซ้อนต่ำกว่าจะถือว่ามีประสิทธิภาพดีกว่า เช่น O(log n) ดีกว่า O(n) ดีกว่า O(n^2) ตามลำดับ การออกแบบ Algorithm จึงมุ่งเน้นให้ได้ความซับซ้อนต่ำที่สุดเท่าที่จะทำได้สรุปได้ว่า ความซับซ้อนของอัลกอริทึมเป็นสิ่งสำคัญที่ช่วยบ่งบอกถึงประสิทธิภาพของอัลกอริทึมนั้นๆ ในการแก้ปัญหา ซึ่งจะส่งผลต่อประสิทธิภาพโดยรวมของระบบหรือโปรแกรมด้วย

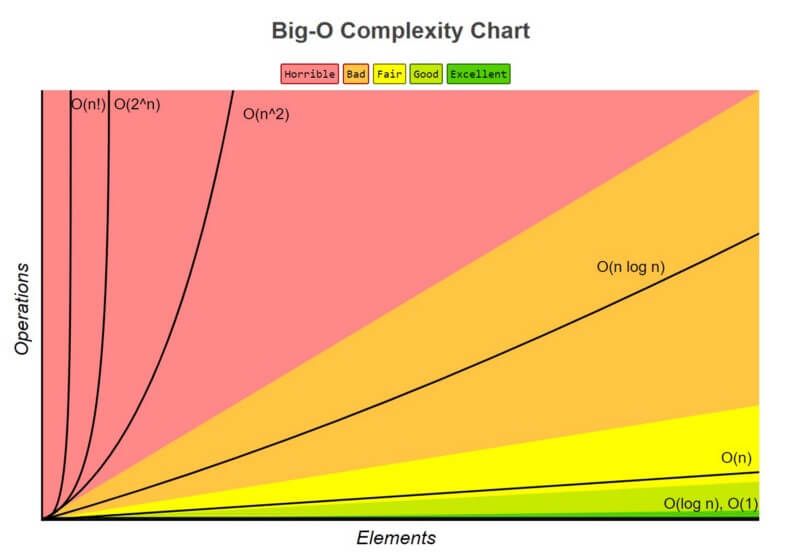
ภาพจาก https://www.devopsschool.com/blog/complete-tutorial-on-big-o-big-oh-notation/

Big-O คืออะไร ?

Big O (Big O Notation) คือการวัดประสิทธิภาพของ Algorithm โดยพิจารณาจากจำนวนครั้งในการประมวลผลสูงสุดเมื่อขนาดของข้อมูลนำเข้า (Input) มีขนาดใหญ่ขึ้น

ความสำคัญของ Big O

• ช่วยให้เราสามารถเปรียบเทียบประสิทธิภาพของอัลกอริทึมต่างๆ ได้ โดยไม่ต้องพึ่งพาปัจจัยอื่นๆ เช่น hardware ระบบปฏิบัติการ ภาษาที่ใช้เขียน เป็นต้น
• ช่วยให้เราสามารถเลือกใช้ Algorithm ที่มีประสิทธิภาพสูงสุดสำหรับงานนั้นๆ ได้
• ในการพัฒนาซอฟต์แวร์ที่มีผู้ใช้งานจำนวนมาก การเลือกใช้อัลกอริทึมที่มีประสิทธิภาพสูงจะช่วยประหยัดต้นทุนในการดำเนินงาน (Operating Cost) ได้มาก

แนวคิดของ Big O Notation มาจากทฤษฎี Asymptotic Analysis ในคณิตศาสตร์ ซึ่งใช้ในการวิเคราะห์พฤติกรรมขีดจำกัดของ function เมื่อตัวแปรมีค่ามากๆ หรือน้อยๆ มากๆ โดย Big O notation แสดงถึง “กรณีที่เลวร้ายที่สุด” (Worst case Scenario) บนขอบเขตของเวลาการทำงานของ Algorithm มันอธิบายถึงเวลาสูงสุดที่ Algorithm อาจใช้สำหรับข้อมูลขนาด n ใดๆออกมา

ยกตัวอย่างเช่น ถ้า Algorithm มีความซับซ้อนด้านเวลาเป็น O(n) หมายความว่าเมื่อขนาดข้อมูล n เพิ่มขึ้น เวลาการทำงานจะเพิ่มขึ้นไม่เกินค่าคงที่บางค่าคูณด้วย n ไปกว่านี้แล้วเป็นต้น

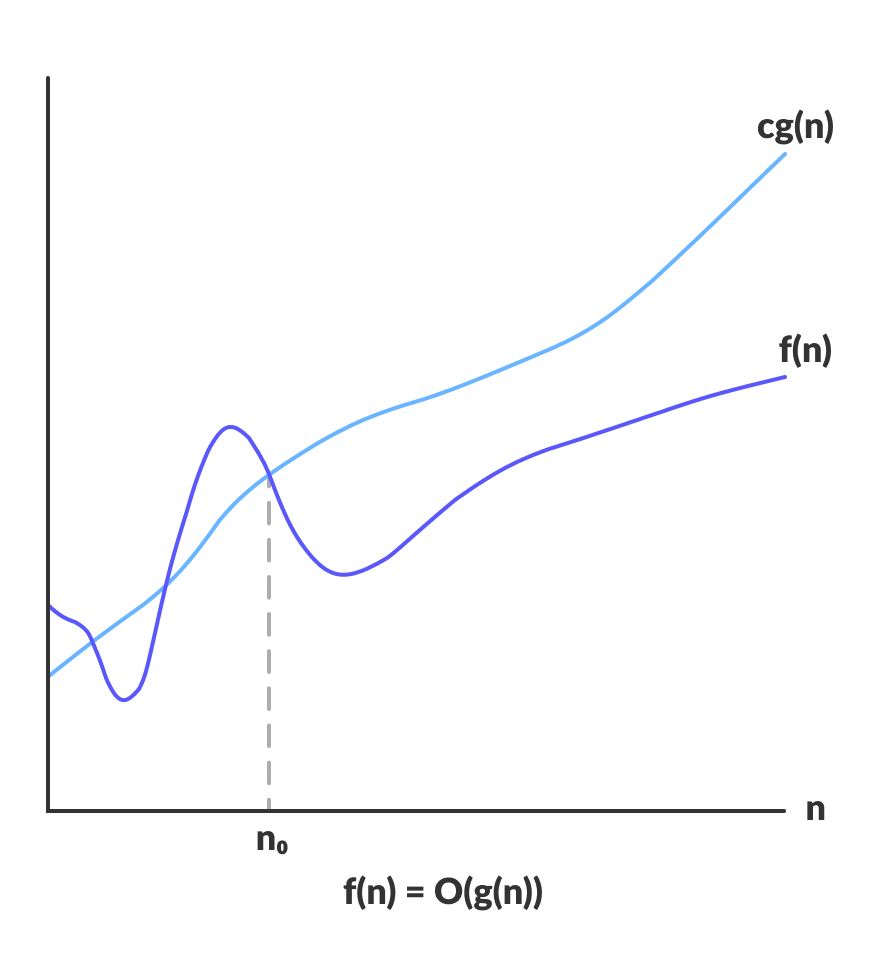
คำถามสำคัญเลยของ Big O คือ “ทำไมเราจึงสามารถใช้ Worst Case อย่าง Big O (จำนวนการทำงานสูงสุดของ Algorithm) มาวิเคราะห์แทนที่จะใช้การคำนวนทั้งหมดออกมาได้” เราจึงจำเป็นต้องพิสูจน์ว่า Big O นั้นได้ cover “จำนวน opration สูงสุดของ algorithm นั้น” ไว้เป็นที่เรียบร้อย

เพื่อให้เกิดความเข้าใจเพิ่มขึ้น เราจะนิยาม algorithm แบบเดียวกันกับ function โดยให้

• f(n) คือจำนวนขั้นตอนการทำงานสูงสุดของอัลกอริทึม
• g(n) คือ function ที่ใช้ประมาณค่าของ f(n) ด้วย Big O Notation [นี่คือตัวที่เราจะใช้] ซึ่งก็คือ Worst case
• n คือขนาดของข้อมูลนำเข้า

ค่าคงที่ c ที่ทำให้จำนวนขั้นตอนการทำงานสูงสุดของ algorithm f(n) มีค่าไม่เกิน c คูณกับ g(n) เมื่อขนาดของข้อมูลนำเข้า n มีค่ามากพอ

การพิสูจน์ว่า f(n) = O(g(n)) จะต้องแสดงให้เห็นว่าสามารถหาค่าคงที่ c และจุดเริ่มต้น n0 ได้ เช่นที่ทำให้

$$0 \leq f(n) \leq cg(n) \; \forall n \geq n_0$$

ค่า c นี้จะเป็นค่าคงที่ในการประมาณค่าของ f(n) ด้วย Big O Notation

ตัวอย่างเช่น ถ้าพิสูจน์ได้ว่า 3n^2 + 2n + 1 = O(n^2) โดยเลือก c = 6 และ n0 = 1 แสดงว่าเมื่อ n ≥ 1 สิ่งนี้จะเป็นจริงเสมอ

$$0 \leq 3n^2 + 2n + 1 \leq 6n^2$$

ดังนั้น จึงสรุปได้ว่า

$$0 \leq f(n) \leq 6n^2 = 6g(n)$$

นั่นคือ f(n) = O(n^2) นั่นเอง แปลไทยง่ายๆว่า เราสามารถใช้ O(n^2) ในการวิเคราะห์ภาพรวมของ Algorithm แทนได้ เนื่องจากจำนวน opration cover “ครบทั้งหมดของ Algorithm” แล้วเรียบร้อยนั่นเอง

ดังนั้น สรุปจุดประสงค์หลักของการวิเคราะห์ Big O ได้ดังนี้

1. เพื่อประเมินประสิทธิภาพของ Algorithm ในแง่ของเวลาและหน่วยความจำที่ใช้ เมื่อขนาดของข้อมูลนำเข้ามีขนาดใหญ่ขึ้น
2. เพื่อเปรียบเทียบประสิทธิภาพของ Algorithm ต่างๆ ได้อย่างเป็นระบบ โดยไม่ต้องพึ่งพาปัจจัยอื่นๆ เช่น ฮาร์ดแวร์ ระบบปฏิบัติการ ภาษาที่ใช้เขียน เป็นต้น
3. ช่วยให้สามารถเลือกใช้ Algorithm ที่มีประสิทธิภาพสูงสุดสำหรับงานนั้นๆ ได้ โดยพิจารณาจากค่า Big O
4. ในการพัฒนาซอฟต์แวร์ที่มีผู้ใช้งานจำนวนมาก การเลือกใช้อัลกอริทึมที่มีประสิทธิภาพสูง (Big O ต่ำ) จะช่วยประหยัดต้นทุนในการดำเนินงาน (Operating Cost) ได้มาก
5. ช่วยให้สามารถประเมินความเหมาะสมระหว่างต้นทุนการพัฒนาและต้นทุนการดำเนินงานได้ เพื่อเลือกใช้อัลกอริทึมที่เหมาะสมกับงานนั้นๆได้