แนะนำ Big O แต่ละแบบ

ประเภทของ Big O

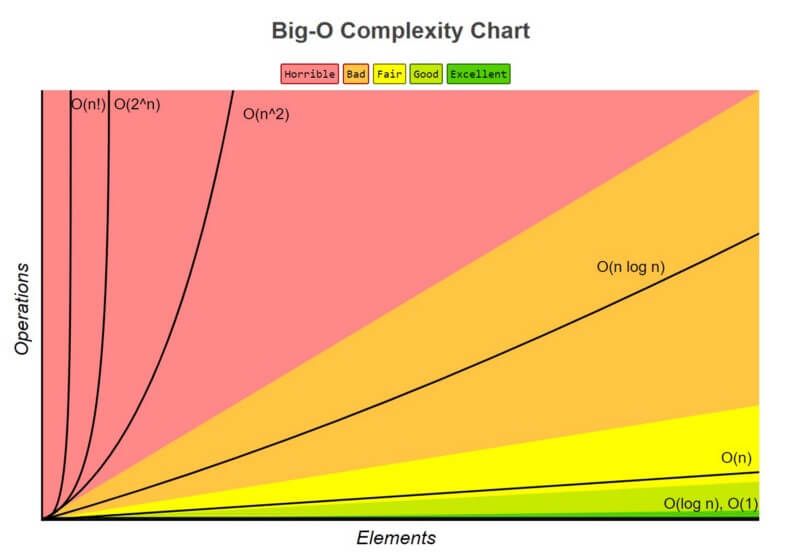
โดยปกติ เพื่อให้เกิดความเข้าใจที่ง่ายขึ้นในการวิเคราะห์ complexity ของ algorithm จึงได้มีการแบ่งประเภท Big O เอาไว้ต่างๆดังนี้ (ไล่จากดีที่สุดไปแย่ที่สุด)

1. O(1) - Constant Time

• เป็น Big O ที่ดีที่สุด ไม่ว่า input จะมีขนาดเท่าไร ระยะเวลาในการประมวลผลจะคงที่เสมอ
• ตัวอย่างเช่น การเข้าถึงข้อมูลใน array ด้วย index, arithmetic operations (+, -, *, /)

2. O(log n) - Logarithmic Time

• เป็น Big O ที่มีประสิทธิภาพดีมาก โดยในแต่ละรอบของ loop จะลดขนาดของปัญหาลงครึ่งหนึ่ง
• ตัวอย่างเช่น binary search, การหารากที่สอง (square root)

3. O(n) - Linear Time

• เวลาในการประมวลผลจะแปรผันตามขนาดของ input โดยตรง
• ตัวอย่างเช่น การวนลูปเพื่อค้นหาค่าใน array, maximum contiguous sum

4. O(n log n) - Linearithmic Time

• เป็นการรวมกันระหว่าง linear และ logarithmic โดยมีลูป n รอบ และในแต่ละรอบใช้เวลา log n
• ตัวอย่างเช่น merge sort, quick sort

5. O(n^2) - Quadratic Time

• เวลาในการประมวลผลจะเพิ่มขึ้นแบบ quadratic เมื่อ input เพิ่มขึ้น
• มักเกิดจากการมี nested loop 2 ชั้น
• ตัวอย่างเช่น bubble sort, selection sort

6. O(2^n) - Exponential Time

• เวลาในการประมวลผลจะเพิ่มขึ้นอย่างรวดเร็วแบบ exponential เมื่อ input มีขนาดใหญ่ขึ้นเพียงเล็กน้อย
• ตัวอย่างเช่น brute force สำหรับ Traveling Salesman Problem

7. O(n!) - Factorial Time

• เป็น Big O ที่แย่ที่สุด ใช้เวลาในการประมวลผลนานมากแม้กับ input ขนาดเล็ก
• ตัวอย่างเช่น การหา permutation ของ set ขนาด n

ตัวอย่าง Code C++ ของแต่ละประเภท

จากทั้งหมด 7 อัน

1. O(1) : Constant Time

ในกรณีนี้ จำนวนคำสั่งที่ทำงานไม่ขึ้นกับขนาดของ input ดังนั้นเวลาในการประมวลผลจึงคงที่ไม่ว่า input จะมีขนาดเท่าใด

int findMax(int a, int b) {
  return (a > b) ? a : b; // ทำงาน 2 คำสั่งเสมอ
}

2. O(log n) : Logarithmic Time

algorithm ที่มีความซับซ้อนในระดับนี้ จะลดขนาดของปัญหาลงครึ่งหนึ่งในแต่ละรอบ ตัวอย่างเช่น Binary Search

int binarySearch(int arr[], int left, int right, int x) {
  if (right >= left) {
    int mid = left + (right - left) / 2;

    if (arr[mid] == x)
      return mid;

    if (arr[mid] > x)
      return binarySearch(arr, left, mid - 1, x);

    return binarySearch(arr, mid + 1, right, x);
  }
  return -1;
}

** ตัวนี้เราจะมาเจาะลึกอีกทีในหัวข้อ Optimize Algorithm ในแต่ละประเภท

3. O(n) : Linear Time

ในกรณีนี้ จำนวนคำสั่งที่ทำงานจะเป็นสัดส่วนโดยตรงกับขนาดของ input ตัวอย่างเช่น Linear Search

int linearSearch(int arr[], int n, int x) {
  for (int i = 0; i < n; i++) // วนลูป n รอบ
    if (arr[i] == x)
      return i;
  return -1;
}

4. O(n log n) : Linearithmic Time

Algorithm ที่มีความซับซ้อนในระดับนี้ จะมี loop แบบ n รอบ ที่มี loop แบบ log n รอบอยู่ข้างใน ตัวอย่างเช่น Merge Sort

void merge(int arr[], int l, int m, int r) {
  int i, j, k;
  int n1 = m - l + 1;
  int n2 = r - m;

  int L[n1], R[n2];

  for (i = 0; i < n1; i++)
    L[i] = arr[l + i];
  for (j = 0; j < n2; j++)
    R[j] = arr[m + 1 + j];

  i = 0;
  j = 0;
  k = l;
  while (i < n1 && j < n2) {
    if (L[i] <= R[j]) {
      arr[k] = L[i];
      i++;
    } else {
      arr[k] = R[j];
      j++;
    }
    k++;
  }

  while (i < n1) {
    arr[k] = L[i];
    i++;
    k++;
  }

  while (j < n2) {
    arr[k] = R[j];
    j++;
    k++;
  }
}

void mergeSort(int arr[], int l, int r) {
  if (l < r) {
    int m = l + (r - l) / 2;

    mergeSort(arr, l, m);
    mergeSort(arr, m + 1, r);

    merge(arr, l, m, r);
  }
}

5. O(n^2) : Quadratic Time

ในกรณีนี้ จำนวนคำสั่งที่ทำงานจะเป็นกำลังสองของขนาด input ตัวอย่างเช่น Bubble Sort

void bubbleSort(int arr[], int n) {
  for (int i = 0; i < n - 1; i++)       // วนลูป n-1 รอบ
    for (int j = 0; j < n - i - 1; j++) // วนลูป n-i รอบ
      if (arr[j] > arr[j + 1])
        swap(arr[j], arr[j + 1]);
}

6. O(2^n) : Exponential Time

Algorithm ที่มีความซับซ้อนในระดับนี้จะมีเวลาทำงานเพิ่มขึ้นเป็นเลขชี้กำลัง ตัวอย่างเช่น การหาค่า Fibonacci แบบเรียกซ้ำ

int fibonacci(int n) {
  if (n <= 1)
    return n;
  return fibonacci(n - 1) + fibonacci(n - 2); // เรียกซ้ำ 2 ครั้ง
}

วิธีการคำนวณ Big O สำหรับ O(2^n) หรือ Exponential Time นั้น มีดังนี้

1. กำหนดให้ n เป็นขนาดของอินพุต
2. หาจำนวนคำสั่งที่ทำงานในแต่ละรอบวนซ้ำ (loop) ในกรณีของ O(2^n) จะมีการแบ่งปัญหาออกเป็น 2 ส่วน แล้วเรียกตัวเองซ้ำสำหรับแต่ละส่วน ดังนั้นจำนวนคำสั่งที่ทำงานจะเป็น 2 เท่าของรอบก่อนหน้า
3. แสดงจำนวนคำสั่งที่ทำงานในรูปแบบของ nเนื่องจากมีการแบ่งปัญหาออกเป็น 2 ส่วนในแต่ละรอบ จำนวนคำสั่งที่ทำงานจึงเป็น 2 เท่าของรอบก่อนหน้า ดังนั้นจำนวนคำสั่งทั้งหมดจะเป็น 2^n

เช่น จากตัวอย่างของ Fibonacci เมื่อ n = 5 จะมีการเรียกซ้ำดังนี้

• fibonacci(5) เรียก fibonacci(4) และ fibonacci(3)
• fibonacci(4) เรียก fibonacci(3) และ fibonacci(2)
• fibonacci(3) เรียก fibonacci(2) และ fibonacci(1)
• …

จะเห็นว่าจำนวนครั้งในการเรียกซ้ำจะเพิ่มขึ้นเป็น 2 เท่าในแต่ละรอบ ดังนั้นจำนวนคำสั่งทั้งหมดจึงมีความซับซ้อน O(2^n) การคำนวณ O(2^n) เมื่อ n = 100,000 จะได้ผลลัพธ์ประมาณ 10^30,104 ซึ่งเป็นจำนวนที่มากมายจนไม่สามารถคำนวณได้ในเวลาอันสั้น ดังนั้นจึงควรหลีกเลี่ยง algorithm ที่มีความซับซ้อนในระดับ O(2^n) เว้นแต่ในกรณีที่ขนาดของ input มีขนาดเล็กมากเท่านั้น จึงจะพอใช้ได้

7. O(n!) : Factorial Time

นี่เป็นความซับซ้อนที่แย่ที่สุด เวลาทำงานจะเพิ่มขึ้นเป็น factorial ของขนาด input ตัวอย่างเช่น การสลับตำแหน่งของสมาชิกในอาร์เรย์ทุกรูปแบบ (permutation)

void permute(int arr[], int l, int r) {
  if (l == r) {
    // แสดงผลลัพธ์
  } else {
    for (int i = l; i <= r; i++) {
      swap(arr[l], arr[i]);
      permute(arr, l + 1, r); // เรียกซ้ำ (n-1)! ครั้ง
      swap(arr[l], arr[i]);   // backtrack
    }
  }
}

Big O Properties

Properties ที่น่าสนใจสำหรับการวิเคราะห์ จะมีประมาณ 3 คุณสมบัตินี้ที่น่าสนใจคือ

• Additive Property = การบวกกันของ Big O
• Transitivity with Multiplicative Constant = การคูณกับค่าคงที่

โดยกำหนดให้

$$f(n) = O(g(n)), h(n) = O(p(n))$$

Additive Property

$$f(n) + h(n) = O(\max(g(n), p(n)))$$

ตัวอย่างของ Big O เคส "Additive Property" สำหรับ C++ คือ

int function1(int n) {
  int count = 0;
  for (int i = 0; i < n; i++) { // O(n)
    count += 1;
  }
  return count;
}

int function2(int n) {
  int count = 0;
  for (int i = 0; i < n; i++) { // O(n)
    count += 2;
  }
  return count;
}

int main() {
  int n = 10;
  int result1 = function1(n); // O(n)
  int result2 = function2(n); // O(n)
  // ผลรวมของ function1 และ function2 คือ O(n) + O(n) = O(n)
  return 0;
}

ในตัวอย่างนี้ function1 และ function2 ต่างก็มีความซับซ้อนเวลาเป็น O(n) เนื่องจากมี loop ที่วนตามขนาดของ n เมื่อเรียกใช้ function1 และ function2 ใน main จะได้ผลรวมของความซับซ้อนเป็น O(n) + O(n) = O(n) ตามคุณสมบัติ Additive Property ของ Big O

คุณสมบัติ Additive Property ของ Big O ระบุว่า ถ้า f(n) = O(g(n)) และ h(n) = O(k(n)) แล้ว f(n) + h(n) = O(max(g(n), k(n)))

ดังนั้นเมื่อ f(n) = O(n) และ h(n) = O(n) จึงได้ f(n) + h(n) = O(max(n, n)) = O(n) การพิจารณาเพียงเทอมสูงสุดนี้เป็นไปตามนิยามของ Big O ที่มุ่งหาขีดจำกัดบนสุดของฟังก์ชันเมื่อ n มีค่ามากๆ โดยไม่สนใจค่าคงที่และเทอมต่ำกว่านั่นเอง

Transitivity with Multiplicative Constant

$$c \cdot f(n) = O(g(n)), c > 0$$

ตัวอย่างของ Big O "Transitivity with Multiplicative Constant" สำหรับ C++ คือ

int function1(int n) {
  int count = 0;
  for (int i = 0; i < 5 * n; i++) { // O(n)
    count += 1;
  }
  return count;
}

int function2(int n) {
  int count = 0;
  for (int i = 0; i < 2 * n; i++) { // O(n)
    for (int j = 0; j < 100; j++) { // O(1)
      count += 1;
    }
  }
  return count;
}

int main() {
  int n = 10;
  int result1 = function1(n); // O(n)
  int result2 = function2(n); // O(n * 1) = O(n)
  // ทั้ง function1 และ function2 มีความซับซ้อน O(n)
  return 0;
}

ในตัวอย่างนี้

• function1 มี loop ที่วน 5*n รอบ ซึ่งเมื่อคำนวณ Big O แล้วจะได้ O(5n) = O(n) เนื่องจากค่าคงที่ 5 จะถูกละทิ้งไปตามคุณสมบัติ Transitivity with Multiplicative Constant ของ Big O
• ส่วน function2 มี loop ชั้นนอกที่วน 2*n รอบ และ loop ชั้นในที่วน 100 รอบ เมื่อคำนวณ Big O จะได้ O(2n * 100) = O(2n) = O(n) เช่นกัน
• ดังนั้น ทั้ง function1 และ function2 จึงมีความซับซ้อนเวลาเป็น O(n) ตามคุณสมบัติของ Additive Property

คุณสมบัติ Transitivity with Multiplicative Constant ของ Big O ระบุว่า ถ้า f(n) = O(g(n)) แล้ว f(n) = c * g(n) เมื่อ c เป็นค่าคงที่

ดังนั้น ถ้า f(n) = O(n) แล้ว f(n) = 5n ก็จะมีความซับซ้อนเป็น O(n) เช่นกัน เนื่องจากค่าคงที่ 5 จะถูกละทิ้งไป

คุณสมบัตินี้เป็นประโยชน์ในการวิเคราะห์ความซับซ้อนของอัลกอริธึม โดยไม่จำเป็นต้องคำนึงถึงค่าคงที่ที่คูณกับฟังก์ชันหลัก ซึ่งช่วยให้การวิเคราะห์ง่ายขึ้น