Sort

การ Sort Algorithm คืออะไร

การ sorting algorithm (หรือ ขั้นตอนวิธีการเรียงลำดับข้อมูล) คือกระบวนการจัดเรียงข้อมูลให้อยู่ในลำดับที่ต้องการ ไม่ว่าจะเป็นการเรียงจากน้อยไปมาก หรือจากมากไปน้อย

ทำไม Sort Algorithm จึงสำคัญ

การจัดเรียงข้อมูล (sorting) เป็นพื้นฐานสำคัญใน computer science และรวมถึงมีการนำไปใช้ในงานหลากหลายรูปแบบ เช่น

• Searching algorithms เช่น Binary Search ที่วิธีการค้นหาแบบนี้จำเป็นต้องใช้ list ที่เรียงลำดับไว้แล้วในการค้นหา
• Data processing and analysis การจัดเรียงข้อมูลช่วยให้การประมวลผลและวิเคราะห์ข้อมูลง่ายและรวดเร็วขึ้น
• Database operations โดยตัว Database นั้นมักจัดเก็บข้อมูลที่เรียงลำดับ เพื่อให้การค้นหาและดึงข้อมูลมีประสิทธิภาพยิ่งขึ้น (เป็นการประยุกต์ใช้ร่วมกันกับ Search)

ดังนั้น การใช้ Algorithm ในการจัดเรียงข้อมูล จึงมีความสำคัญต่อการเพิ่มประสิทธิภาพในการทำงานของงานคำนวณต่างๆออกมาได้ด้วยเช่นกัน

Types of Sorting Algorithms

Sorting algorithms สามารถแบ่งออกเป็นสองประเภทหลักคือ

1. Comparison-based sorting algorithms: algorithms เหล่านี้จะเปรียบเทียบข้อมูลเพื่อกำหนดลำดับที่สัมพันธ์กัน ตัวอย่างเช่น bubble sort, insertion sort, selection sort, merge sort, quicksort, heapsort
2. Non-comparison-based sorting algorithms algorithmsเหล่านี้จะไม่ใช้การเปรียบเทียบเพื่อกำหนดลำดับของข้อมูล แต่ใช้ประโยชน์จากคุณสมบัติเฉพาะของข้อมูล เช่น ช่วงของค่าหรือการกระจายของข้อมูล มาเป็นตัวชี้วัดในการจัดเรียงแทน ตัวอย่างเช่น counting sort, radix sort, bucket sort

โดยในหัวข้อนี้เราจะ focus กันอยุ่ที่ Comparison-based sorting algorithms กันก่อน ซึ่งเป็นพื้นฐานสำคัญที่จะนำไปสู่ Algorith ประเภทอื่นๆด้วย

ประเภทของการ Sort

นี่คือประเภทที่แยกตามรูปแบบการเรียงของ Sorting Algorithm จะมีดังนี้

1. Bubble Sort วิธีนี้จะเปรียบเทียบข้อมูลที่อยู่ติดกัน แล้วสลับตำแหน่งของข้อมูลคู่นั้นหากเรียงลำดับไม่ถูกต้อง ทำซ้ำไปเรื่อยๆ จนข้อมูลทั้งหมดเรียงลำดับเสร็จ
2. Insertion Sort วิธีนี้จะค่อยๆ สร้างแถวข้อมูลที่เรียงลำดับเสร็จทีละหนึ่งข้อมูล โดยนำข้อมูลแต่ละตัวไปแทรกไว้ในตำแหน่งที่ถูกต้องภายในแถวข้อมูลที่เรียงลำดับเสร็จแล้ว
3. Selection Sort วิธีนี้จะหาข้อมูลที่น้อยที่สุด (หรือมากที่สุด) ภายในแถวข้อมูลที่ยังไม่เรียงลำดับ แล้วนำไปสลับตำแหน่งกับข้อมูลตัวแรกในแถวข้อมูลที่ยังไม่เรียงลำดับ ทำซ้ำไปเรื่อยๆ จนข้อมูลทั้งหมดเรียงลำดับเสร็จ
4. Merge Sort วิธีนี้แบ่งแยก (divide-and-conquer) ข้อมูลออกเป็นสองส่วน ย่อยข้อมูลทั้งสองส่วนนั้นอีก แล้วจึงนำข้อมูลที่ย่อยเสร็จแล้วแต่ละส่วนมาผสาน (merge) เข้าด้วยกันเพื่อให้ได้ข้อมูลที่เรียงลำดับแล้วออกมา
5. Quicksort วิธีนี้แบ่งแยก (divide-and-conquer) ข้อมูลโดยอาศัยข้อมูลตัวหนึ่งเป็นจุดอ้างอิง (pivot) แบ่งข้อมูลออกเป็นสองส่วน คือ ข้อมูลที่น้อยกว่าจุดอ้างอิงและข้อมูลที่มากกว่าหรือเท่ากับจุดอ้างอิง แล้วจึงเรียงลำดับข้อมูลทั้งสองส่วนนั้น
6. Heapsort วิธีนี้สร้างโครงสร้างข้อมูลแบบ heap จากข้อมูลที่ต้องการเรียงลำดับ จากนั้นดึงข้อมูลที่ใหญ่ที่สุด (หรือเล็กที่สุด) ออกจาก heap ทีละตัวเพื่อสร้างแถวข้อมูลที่เรียงลำดับออกมา

สำหรับพื้นฐานหัวข้อนี้เราจะคุยกัน 3 Sort แรกก่อนคือ Bubble Sort, Insertion Sort และ Selection Sort สำหรับ Sort 3 ตัวที่เหลือ เราจะยกไปคุยใน Session ที่เกี่ยวข้องกับเรื่องนั้นๆอีกที

Bubble Sort

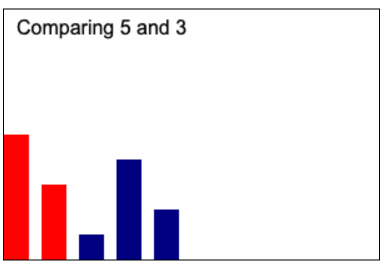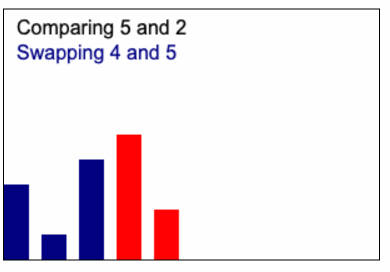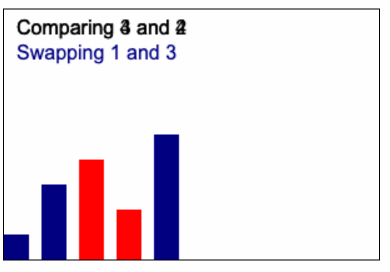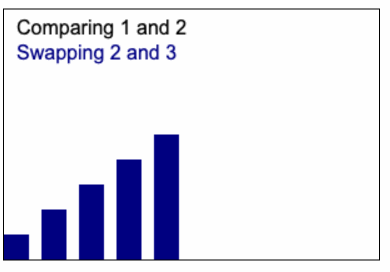
Bubble sort เป็นขั้นตอนการเรียงลำดับ โดยจะเปรียบเทียบข้อมูลที่อยู่ติดกันเป็นคู่ๆ แล้วสลับตำแหน่งของข้อมูลคู่นั้น หากเรียงลำดับไม่ถูกต้อง วิธีนี้เปรียบเหมือนกับการ "bubbling" ข้อมูลขนาดใหญ่นั้นขึ้นไปยังด้านบนสุดของแถวข้อมูล

หลักการทำงานของ Bubble sort คือ

1. เปรียบเทียบข้อมูลสองตัวแรกที่อยู่ติดกันในแถวข้อมูล
2. ถ้า ข้อมูลตัวแรกมากกว่าข้อมูลตัวที่สอง ให้สลับตำแหน่งของข้อมูลทั้งสอง
3. เลื่อนไปเปรียบเทียบกับข้อมูลคู่ถัดไปที่อยู่ติดกัน
4. ทำซ้ำขั้นตอนที่ 1-3 ไปจนกว่าจะถึงข้อมูลตัวสุดท้ายของแถวข้อมูล
5. หลังจากผ่านไปหนึ่งรอบ ข้อมูลตัวที่ใหญ่ที่สุดจะถูกย้ายไปอยู่ในตำแหน่งที่ถูกต้องที่ด้านบนสุดของแถวข้อมูลแล้ว
6. ทำซ้ำขั้นตอนที่ 1-5 สำหรับข้อมูลที่เหลือที่ยังไม่เรียงลำดับจนกว่าแถวข้อมูลทั้งหมดจะเรียงลำดับเสร็จ

ไอเดียก็จะเหมือนกับ Animation นี้

code c++ bubble sort จะมีหน้าตาประมาณนี้

#include <iostream>
#include <vector>
using namespace std;

void bubbleSort(vector<int> &arr) {
  int n = arr.size();
  bool swapped;

  for (int i = 0; i < n - 1; i++) {
    swapped = false;
    for (int j = 0; j < n - i - 1; j++) {
      if (arr[j] > arr[j + 1]) {
        // Swap arr[j] and arr[j+1]
        int temp = arr[j];
        arr[j] = arr[j + 1];
        arr[j + 1] = temp;
        swapped = true;
      }
    }

    // Visualize current state of array
    cout << "Pass " << i + 1 << ": ";
    for (int k = 0; k < n; k++) {
      cout << arr[k] << " ";
    }
    cout << "\n";

    // If no swaps occurred, array is sorted
    if (!swapped)
      break;
  }
}

int main() {
  vector<int> arr = {5, 3, 1, 4, 2};

  cout << "Initial Array: ";
  for (int i = 0; i < arr.size(); i++) {
    cout << arr[i] << " ";
  }
  cout << "\n\n";

  bubbleSort(arr);

  cout << "\nSorted Array: ";
  for (int i = 0; i < arr.size(); i++) {
    cout << arr[i] << " ";
  }

  return 0;
}

ผลลัพธ์

Initial Array: 5 3 1 4 2 

Pass 1: 3 1 4 2 5 # 5 เรียง
Pass 2: 1 3 2 4 5 # 4 5 เรียง
Pass 3: 1 2 3 4 5 # 3 4 5 เรียง
Pass 4: 1 2 3 4 5 # 2 3 4 5 เรียง

Sorted Array: 1 2 3 4 5

Insertion Sort

Insertion sort เป็นอีกหนึ่งขั้นตอนการเรียงลำดับข้อมูล วิธีนี้จะค่อยๆ สร้างแถวข้อมูลที่เรียงลำดับเสร็จทีละหนึ่งข้อมูล โดยเปรียบเทียบข้อมูลแต่ละตัวกับข้อมูลที่เรียงลำดับเสร็จแล้ว แล้วนำไปแทรกไว้ในตำแหน่งที่ถูกต้องได้

หลักการทำงานของ Insertion sort คือ

1. เริ่มต้นโดยถือว่าข้อมูลตัวแรกเป็นแถวข้อมูลย่อย ที่เรียงลำดับเสร็จแล้ว
2. สำหรับข้อมูลแต่ละตัวที่เหลือ นำไปเปรียบเทียบกับข้อมูลในแถวข้อมูลย่อยที่เรียงลำดับเสร็จแล้ว
3. ถ้า ข้อมูลที่นำไปเปรียบเทียบ มีค่า น้อยกว่า ข้อมูลทางด้านซ้ายของมัน > ให้เลื่อนข้อมูลในแถวข้อมูลย่อยที่เรียงลำดับเสร็จแล้ว ไปทางขวา ทีละ 1 ตำแหน่ง
4. ทำการเลื่อนข้อมูลอย่างต่อเนื่องจนกว่าจะเจอตำแหน่งที่ เหมาะสม หรือจนกว่าจะถึง ตำแหน่งแรก ของแถวข้อมูลทั้งหมด
5. นำข้อมูลที่นำไปเปรียบเทียบ แทรก เข้าไปใน ตำแหน่งที่เหมาะสม ภายในแถวข้อมูลย่อยที่เรียงลำดับเสร็จแล้ว
6. ทำซ้ำขั้นตอนที่ 2-5 สำหรับข้อมูลที่เหลือทั้งหมดจนกว่าจะเรียงลำดับข้อมูลทั้งแถวเสร็จ

ไอเดียก็จะเหมือนกับ Animation นี้

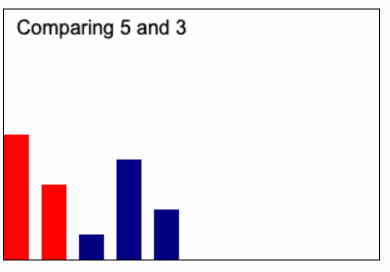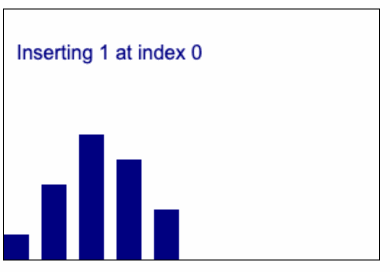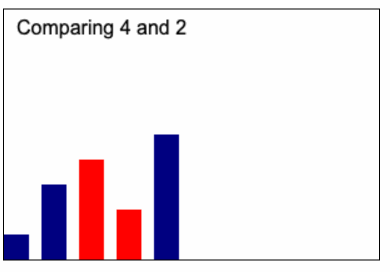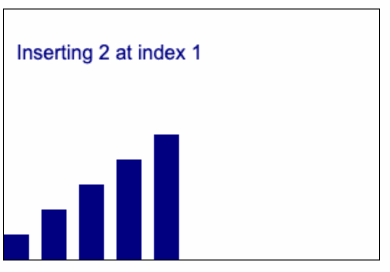
code insertion sort

#include <iostream>
#include <vector>
using namespace std;

void insertionSort(vector<int> &arr) {
  int n = arr.size();

  for (int i = 1; i < n; i++) {
    int key = arr[i];
    int j = i - 1;

    // Move elements of arr[0..i-1], that are greater than key, to one position
    // ahead of their current position
    while (j >= 0 && arr[j] > key) {
      arr[j + 1] = arr[j];
      j--;
    }

    // Insert key into the sorted part
    arr[j + 1] = key;

    // Print current state of array
    cout << "Pass " << i << ": ";
    for (int k = 0; k < n; k++) {
      cout << arr[k] << " ";
    }
    cout << "\n";
  }
}

int main() {
  vector<int> arr = {5, 3, 1, 4, 2};

  cout << "Initial Array: ";
  for (int i = 0; i < arr.size(); i++) {
    cout << arr[i] << " ";
  }
  cout << "\n\n";

  insertionSort(arr);

  cout << "\nSorted Array: ";
  for (int i = 0; i < arr.size(); i++) {
    cout << arr[i] << " ";
  }

  return 0;
}

ผลลัพธ์

Initial Array: 5 3 1 4 2 

Pass 1: 3 5 1 4 2 
Pass 2: 1 3 5 4 2 
Pass 3: 1 3 4 5 2 
Pass 4: 1 2 3 4 5 

Sorted Array: 1 2 3 4 5 

Selection Sort

Selection sort คือ Algorithm สำหรับจัดเรียงที่ทำงานโดยการค้นหาค่าที่เล็กที่สุด (หรือมากที่สุด ขึ้นอยู่กับการจัดเรียงจากน้อยไปมากหรือมากไปน้อย) ในแต่ละรอบจากกลุ่มข้อมูลที่ยังไม่ได้จัดเรียง แล้วสลับตำแหน่งของค่าที่เล็กที่สุดนั้นไปไว้ที่ตำแหน่งแรกของกลุ่มข้อมูลที่ยังไม่ได้จัดเรียง

หลักการทำงานของ Selection sort คือ

1. หาค่าที่เล็กที่สุดในกลุ่มข้อมูลที่ยังไม่ได้จัดเรียง
2. สลับตำแหน่งของค่าที่เล็กที่สุดนั้นไปไว้ที่ตำแหน่งแรกของกลุ่มข้อมูลที่ยังไม่ได้จัดเรียง
3. ทำซ้ำขั้นตอนที่ 1 และ 2 จนกว่าจะจัดเรียงข้อมูลทั้งหมดเสร็จสิ้น

ไอเดียก็จะเหมือนกับ Animation นี้

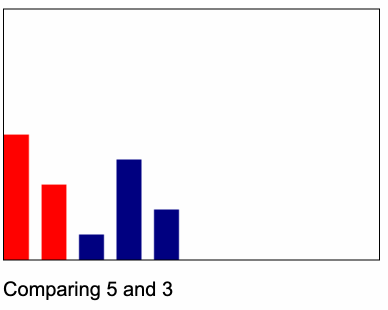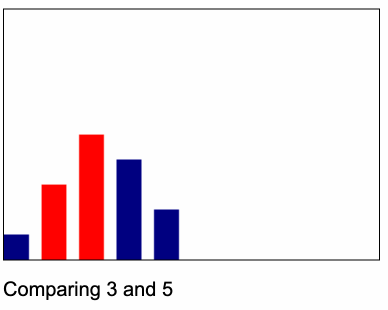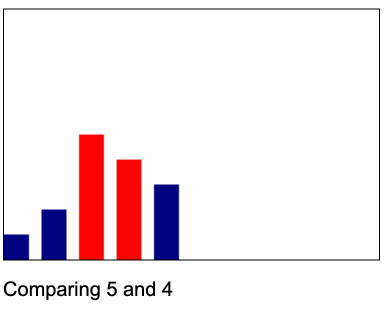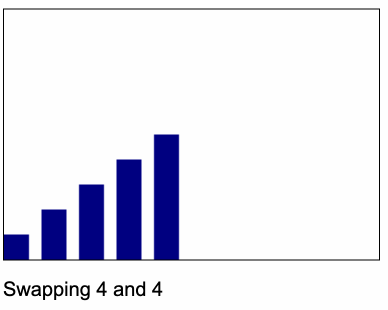
code c++ selection sort

#include <iostream>
#include <vector>
using namespace std;

void selectionSort(vector<int> &arr) {
  int n = arr.size();

  for (int i = 0; i < n - 1; i++) {
    // Find the minimum element in unsorted array
    int minIndex = i;
    for (int j = i + 1; j < n; j++) {
      if (arr[j] < arr[minIndex]) {
        minIndex = j;
      }
    }

    // Swap the found minimum element with the first element
    int temp = arr[minIndex];
    arr[minIndex] = arr[i];
    arr[i] = temp;

    // Print current state of array
    cout << "Pass " << i + 1 << ": ";
    for (int k = 0; k < n; k++) {
      cout << arr[k] << " ";
    }
    cout << "\n";
  }
}

int main() {
  vector<int> arr = {5, 3, 1, 4, 2};

  cout << "Initial Array: ";
  for (int i = 0; i < arr.size(); i++) {
    cout << arr[i] << " ";
  }
  cout << "\n\n";

  selectionSort(arr);

  cout << "\nSorted Array: ";
  for (int i = 0; i < arr.size(); i++) {
    cout << arr[i] << " ";
  }

  return 0;
}

ผลลัพธ์

Initial Array: 5 3 1 4 2 

Pass 1: 1 3 5 4 2 
Pass 2: 1 2 5 4 3 
Pass 3: 1 2 3 4 5 
Pass 4: 1 2 3 4 5 

Sorted Array: 1 2 3 4 5