Tree

Tree คืออะไร

โครงสร้างข้อมูลแบบต้นไม้ (Tree) คือรูปแบบการจัดเก็บข้อมูลที่มีลำดับชั้นเลียนแบบโครงสร้างที่มีการแตกแขนง โดยประกอบด้วยจุดเชื่อมต่อที่เรียกว่า "โหนด" (node) และเส้นเชื่อมโยงระหว่างโหนดที่เรียกว่า "ขอบ" (edge) โครงสร้างแบบต้นไม้เหมาะสำหรับการแสดงและจัดการข้อมูลที่มีความสัมพันธ์แบบบนลงล่าง ในต้นไม้แต่ละโหนดจะมีโหนดลูกได้ตั้งแต่ศูนย์ตัวขึ้นไป ทำให้มันแตกต่างจากโครงสร้างข้อมูลเชิงเส้นอย่างอาร์เรย์ (array) หรือลิงก์ลิสต์ (linked lists) ที่ข้อมูลเชื่อมกันเป็นเส้นตรง

แนวคิดหลักของต้นไม้

โครงสร้างข้อมูลแบบลำดับชั้น Tree จะจัดเรียงข้อมูลแบบมีลำดับชั้น โดยแต่ละสมาชิกจะมีความสัมพันธ์แบบ Parent - child ต่างจากโครงสร้างข้อมูลเชิงเส้นอย่าง Array หรือ Linked List
Node เป็นส่วนประกอบพื้นฐานของต้นไม้ แต่ละโหนดจะเก็บข้อมูลและมี pointer เชื่อมไปยัง child node ต่างๆ
Root Node คือ node บนสุดของต้นไม้และจะไม่มีโหนดพ่อ (parent)
Child Node โหนดที่เชื่อมต่ออยู่ใต้โหนดพ่อโดยตรง
Leaf Node โหนดที่อยู่ปลายสุดของต้นไม้และไม่มีโหนดลูก
Edge เส้นเชื่อมโยงหรือตัวชี้ระหว่างแต่ละโหนด

Tree Representations in C++

ถึงแม้ว่าภาษา C++ จะไม่มีโครงสร้างข้อมูลแบบต้นไม้ (tree) ติดมากับตัวภาษาโดยตรง แต่โดยทั่วไป เราจะสามารถสร้างและจำลองโครงสร้างต้นไม้ได้โดยใช้ "โหนด" (nodes) และ "ตัวชี้" (pointers)

struct Node {
    int data; 
    Node* left; 
    Node* right; 
};

Basic Tree Code

ตัวอย่างการสร้างต้นไม้แบบทวิภาค (Binary Tree) เบื้องต้นในภาษา C++ พร้อมกับฟังก์ชันสำหรับการเพิ่มข้อมูล, การท่องไปในต้นไม้แบบ inorder และตัวอย่างการใช้งานอย่างง่าย:

#include <iostream>
using namespace std;

struct Node {
  int data;
  Node *left;
  Node *right;
};

// Function to create a new node
Node *newNode(int data) {
  Node *node = new Node();
  node->data = data;
  node->left = node->right = nullptr;
  return node;
}

// Function to insert a node in a binary search tree (BST)
void insert(Node *&root, int data) {
  if (root == nullptr) {
    root = newNode(data);
    return;
  }

  if (data < root->data) {
    insert(root->left, data);
  } else {
    insert(root->right, data);
  }
}

// Function for inorder traversal (left, root, right)
void inorderTraversal(Node *root) {
  if (root == nullptr) {
    return;
  }

  inorderTraversal(root->left);
  cout << root->data << " ";
  inorderTraversal(root->right);
}

int main() {
  Node *root = nullptr;

  insert(root, 10);
  insert(root, 5);
  insert(root, 15);
  insert(root, 8);

  cout << "Inorder Traversal: ";
  inorderTraversal(root);
  cout << endl;

  return 0;
}

คำอธิบาย

โครงสร้างโหนด (Node Struct): ส่วนนี้จะนิยามโครงร่างของแต่ละโหนด โดยจะมีข้อมูลอยู่ภายใน พร้อมกับตัวชี้ไปยังโหนดลูกทางซ้าย และโหนดลูกทางขวา
newNode: ฟังก์ชันนี้ทำหน้าที่ช่วยสร้างโหนดใหม่และกำหนดค่าเริ่มต้นให้
insert: ฟังก์ชันสำหรับการเพิ่มโหนดเข้าไปในต้นไม้แบบทวิภาคค้นหา (Binary Search Tree) โดยจะเปรียบเทียบข้อมูลของโหนดที่ต้องการใส่กับโหนดปัจจุบัน และวางลงในฝั่งซ้ายหรือขวาให้เหมาะสม กระบวนการนี้ทำซ้ำแบบเรียกซ้ำ (recursive)
inorderTraversal: ฟังก์ชันสำหรับการ "ท่องไปในต้นไม้" ตามลำดับแบบ inorder (ฝั่งซ้ายของต้นไม้ -> โหนดราก -> ฝั่งขวาของต้นไม้) โดยเป็นฟังก์ชันแบบเรียกซ้ำ (recursive) เช่นกัน
main: เป็นส่วนของโปรแกรมหลัก ทำหน้าที่สร้างตัวอย่างต้นไม้โดยเพิ่มโหนดต่างๆ เข้าไป และแสดงให้เห็นวิธีใช้งานฟังก์ชัน inorderTraversal (ท่องไปในต้นไม้แบบ inorder)

ประเด็นสำคัญ

ต้นไม้แบบทวิภาคค้นหา (Binary Search Tree): ฟังก์ชัน "insert" จะรักษาคุณสมบัติของต้นไม้แบบทวิภาคค้นหา เพื่อให้การค้นหาข้อมูลมีประสิทธิภาพ
การเรียกซ้ำ (Recursion): ฟังก์ชัน "insert" และ "inorderTraversal" ใช้การเรียกซ้ำเพื่อให้การเขียนโปรแกรมกระชับและเข้าใจง่าย

หน้าตา Tree

  (10)
 /    \ 
(5)  (15)
  \
  (8)

ผลลัพธ์

Inorder Traversal: 5 8 10 15

Tree Traversal

การสำรวจต้นไม้ (Traversal) คือกระบวนการที่เข้าไปเยี่ยมชมทุกๆ โหนดในต้นไม้ และดำเนินการบางอย่าง (เช่น การพิมพ์ค่าที่เก็บอยู่ในโหนด) ที่โหนดแต่ละตัว เนื่องจากต้นไม้เป็นโครงสร้างข้อมูลแบบไม่เป็นเส้นตรง (non-linear) เราจึงมีหลายวิธีในการสำรวจต้นไม้

โดยในหัวข้อนี้ เราจะขอพูดถึงพื้นฐาน 2 ตัวที่ใช้สำหรับการค้นหาคือ BFS และ DFS

Breadth-First Search (BFS)

ประเภทของการสำรวจต้นไม้ (Traversal Technique): BFS ย่อมาจาก Breadth-first Search เป็นหนึ่งในอัลกอริทึมสำหรับการสำรวจต้นไม้และกราฟ โดยจะสำรวจ "ตามความกว้าง" ของต้นไม้ก่อน ค่อยๆ ไล่ลงไปทีละระดับ เริ่มจากสำรวจโหนดที่อยู่ใกล้กับโหนดรากก่อน แล้วจึงค่อยไปยังโหนดที่อยู่ห่างออกไป
กลไกการทำงาน: BFS ใช้โครงสร้างข้อมูลแบบคิว (queue) ในการทำงาน โดยมีขั้นตอนดังนี้

เริ่มต้นที่โหนดราก (root node) และเพิ่มลงไปในคิว
ทำซ้ำ (Loop) ตราบใดที่คิวยังไม่ว่าง:

ดึงโหนดแรกสุดของคิวออก ("dequeue")
ประมวลผลโหนดนั้น (เช่น แสดงผล, ทำการคำนวณ เป็นต้น)
เพิ่มโหนดลูกทั้งหมดที่ยังไม่เคยถูกสำรวจลงไปด้านท้ายของคิว ("enqueue")

การใช้กับต้นไม้โดยตรง: เนื่องจากต้นไม้ถือเป็นกราฟชนิดหนึ่ง เราสามารถใช้หลักการสำรวจแบบ BFS ในการสำรวจต้นไม้ได้โดยตรง โดยที่การสำรวจจะเกิดขึ้นแบบไล่ระดับ (level-by-level)

#include <iostream>
#include <queue>

using namespace std;

struct Node {
  int data;
  Node *left;
  Node *right;
};

void breadthFirstSearch(Node *root) {
  if (root == nullptr) {
    return; // Handle empty tree case
  }

  queue<Node *> q;
  q.push(root);

  while (!q.empty()) {
    Node *currentNode = q.front();
    q.pop();

    cout << currentNode->data << " "; // Process the current node

    // Enqueue children (if they exist)
    if (currentNode->left != nullptr) {
      q.push(currentNode->left);
    }
    if (currentNode->right != nullptr) {
      q.push(currentNode->right);
    }
  }
}

int main() {
  // Example tree construction (you'll likely have a different tree)
  Node *root = new Node{1};
  root->left = new Node{2};
  root->right = new Node{3};
  root->left->left = new Node{4};
  root->left->right = new Node{5};

  breadthFirstSearch(root);
  cout << endl;

  return 0;
}

Explanation

ฟังก์ชัน breadthFirstSearch
- รับค่าโหนดราก (root) ของต้นไม้เป็นตัวแปรขาเข้า
- สร้างคิว (queue) ที่มีชื่อว่า q เพื่อใช้ในการสำรวจแบบ BFS
- เริ่มต้นด้วยการเพิ่มโหนดราก (root) ลงไปในคิว
- เข้าสู่วงวน (loop) ที่จะทำงานไปเรื่อยๆ จนกว่าคิวจะว่าง โดยในแต่ละรอบของวงวนจะทำดังนี้:
  - นำโหนดที่อยู่หน้าสุดในคิวออก (q.pop())
  - พิมพ์ค่าข้อมูลที่อยู่ในโหนดออกมา (เปรียบเสมือนการ "เยี่ยมชม" โหนดนั้น)
  - เพิ่มโหนดลูกทางซ้ายและขวา (ถ้ามี) ลงไปในคิวด้วย
ฟังก์ชัน main
- ทำหน้าที่ในการสร้างตัวอย่างของต้นไม้ขึ้นมา
- เรียกใช้ฟังก์ชัน breadthFirstSearch เพื่อทำการสำรวจต้นไม้แบบ BFS

หน้าตาของ Tree

     (1)
    /  \
  (2)  (3)
  / \
(4) (5)

result

1 2 3 4 5

Depth-First Search (DFS)

ประเภทของการสำรวจต้นไม้ (Traversal Technique): DFS ย่อมาจาก Depth-first Search เป็นหนึ่งในอัลกอริทึมสำหรับการสำรวจต้นไม้และกราฟ โดยจะเน้นการสำรวจลงไปใน "แนวลึก" ของต้นไม้ให้ถึงที่สุดก่อน แล้วค่อยย้อนกลับและขยายออกไปสำรวจโหนดอื่นๆภายหลัง
กลไกการทำงาน: การสำรวจแบบ DFS สามารถทำได้โดยใช้ทั้งการเรียกซ้ำ (recursion) หรือใช้โครงสร้างข้อมูลแบบสแต็ก (stack) ดังนี้:
วิธีใช้การเรียกซ้ำ:
1. เริ่มต้นที่โหนดราก (root node)
2. "เยี่ยมชม" โหนดปัจจุบัน (ทำการประมวลผล)
3. เรียกใช้ฟังก์ชัน DFS แบบเรียกซ้ำ โดยใส่โหนดลูกทางซ้ายลงไป (ถ้ามี)
4. เรียกใช้ฟังก์ชัน DFS แบบเรียกซ้ำ โดยใส่โหนดลูกทางขวาลงไป (ถ้ามี)
วิธีใช้สแต็ก (ทำซ้ำ):
1. เริ่มต้นด้วยการเพิ่มโหนดราก (root node) ลงไปในสแต็ก
2. ทำซ้ำ (Loop) ตราบใดที่สแต็กยังไม่ว่าง:
  - นำโหนดบนสุดของสแต็กออก ("Pop")
  - ประมวลผลโหนดนั้น
  - เพิ่มโหนดลูกทางขวา (ถ้ามี) ลงไปในสแต็ก
  - เพิ่มโหนดลูกทางซ้าย (ถ้ามี) ลงไปในสแต็ก
การใช้กับต้นไม้โดยตรง: เนื่องจากการเรียกซ้ำมีวิธีคิดที่สอดคล้องกับโครงสร้างของต้นไม้อยู่แล้ว การใช้ DFS ร่วมกับการเรียกซ้ำจึงเป็นวิธีที่เข้าใจง่ายและเป็นธรรมชาติในการสำรวจต้นไม้

#include <iostream>

using namespace std;

struct Node {
  int data;
  Node *left;
  Node *right;
};

void depthFirstSearch(Node *node) {
  if (node == nullptr) {
    return; // Handle empty subtree case
  }

  cout << node->data << " "; // Process the current node

  // Recursive calls to explore the depth
  depthFirstSearch(node->left);
  depthFirstSearch(node->right);
}

int main() {
  // Example tree construction
  Node *root = new Node{1};
  root->left = new Node{2};
  root->right = new Node{3};
  root->left->left = new Node{4};
  root->left->right = new Node{5};

  depthFirstSearch(root);
  cout << endl;

  return 0;
}

คำอธิบาย

ฟังก์ชัน depthFirstSearch
- รับค่าตัวชี้ (pointer) ของโหนด (Node) เป็นตัวแปรขาเข้า
- ตรวจสอบว่าโหนดปัจจุบันมีค่าว่างหรือไม่ (เงื่อนไขหยุดการเรียกซ้ำ)
- พิมพ์ค่าข้อมูลที่อยู่ในโหนดออกมา (เปรียบเสมือนการ "เยี่ยมชม" โหนดนั้น)
- เรียกใช้ฟังก์ชัน depthFirstSearch แบบเรียกซ้ำ (recursion) กับโหนดลูกทางซ้ายและขวาเพื่อสำรวจต้นไม้ต่อไปในแนวลึก
ฟังก์ชัน main
- ทำหน้าที่ในการสร้างตัวอย่างของต้นไม้ขึ้นมา
- เรียกใช้ฟังก์ชัน depthFirstSearch เพื่อทำการสำรวจต้นไม้แบบ DFS

หน้าตาของ Tree

     (1)
    /  \
  (2)  (3)
  / \
(4) (5)

result

1 2 4 5 3

หรือใช้ stack ก็ได้

#include <iostream>
#include <stack>

using namespace std;

struct Node {
  int data;
  Node *left;
  Node *right;
};

void depthFirstSearchIterative(Node *root) {
  if (root == nullptr) {
    return;
  }

  stack<Node *> s;
  s.push(root);

  while (!s.empty()) {
    Node *currentNode = s.top();
    s.pop();

    cout << currentNode->data << " "; // Process the current node

    // Push children in reverse order (right first, then left)
    // This maintains the equivalent order of a recursive DFS
    if (currentNode->right != nullptr) {
      s.push(currentNode->right);
    }
    if (currentNode->left != nullptr) {
      s.push(currentNode->left);
    }
  }
}

int main() {
  // Example tree construction
  Node *root = new Node{1};
  root->left = new Node{2};
  root->right = new Node{3};
  root->left->left = new Node{4};
  root->left->right = new Node{5};

  depthFirstSearchIterative(root);
  cout << endl;

  return 0;
}

คำอธิบาย

1. ฟังก์ชัน depthFirstSearchIterative

รับค่าโหนดราก (root node) ของต้นไม้เป็นตัวแปรขาเข้า
สร้างสแต็ก (stack) เพื่อเก็บโหนดต่างๆ ไว้
เริ่มต้นด้วยการเพิ่มโหนดรากเข้าไปในสแต็ก

2. วงวน (Loop):

จะทำงานไปเรื่อยๆ ตราบใดที่สแต็กยังไม่ว่าง โดยแต่ละรอบของวงวนจะทำดังนี้:
- นำโหนดบนสุดของสแต็กออก (s.pop())
- พิมพ์ค่าข้อมูลที่อยู่ในโหนดออกมา (เปรียบเสมือนการ "เยี่ยมชม" โหนดนั้น)
- เพิ่มโหนดลูกทางขวา (ถ้ามี) ลงไปในสแต็ก
- เพิ่มโหนดลูกทางซ้าย (ถ้ามี) ลงไปในสแต็ก

3. แนวคิดสำคัญ: การที่เราใส่โหนดลูกทางขวาก่อนลูกทางซ้าย ทำให้ลูกทางซ้ายจะอยู่ด้านบนสุดของสแต็กในภายหลัง ส่งผลให้เกิดการสำรวจแบบลึกลงไป (depth-first) เหมือนกับการใช้ DFS แบบเรียกซ้ำ

ทำไมต้องใช้สแต็กกับ DFS?

วิธีที่ไม่ใช้การเรียกซ้ำ: การใช้สแต็กทำให้เราใช้ DFS ได้โดยไม่ต้องพึ่งการเรียกซ้ำของฟังก์ชัน ซึ่งอาจจะเป็นประโยชน์ในบางกรณีที่การเรียกซ้ำอาจทำให้เกิด stack overflow
ควบคุมได้ละเอียดขึ้น: สแต็กทำให้เราสามารถควบคุมลำดับการสำรวจต้นไม้ได้อย่างละเอียดมากขึ้น หากต้องการปรับแต่งอัลกอริทึมให้ต่างออกไป

Tree Type

1. ต้นไม้แบบทวิภาค (Binary Tree)

แต่ละโหนดมีโหนดลูกได้มากสุดสองโหนด (ลูกทางซ้าย และ ลูกทางขวา)
ใช้ใน: ต้นไม้ค้นหาแบบทวิภาค (Binary Search Tree), Expression Trees, Heaps

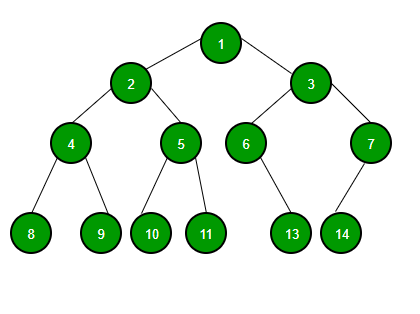
ภาพจาก https://www.geeksforgeeks.org/binary-tree-data-structure/

2. ต้นไม้ค้นหาแบบทวิภาค (Binary Search Tree - BST)

เป็นต้นไม้แบบทวิภาคที่มีคุณสมบัติพิเศษในการเรียงลำดับข้อมูล
ค่าของโหนดลูกทางซ้าย < ค่าของโหนดปัจจุบัน < ค่าของโหนดลูกทางขวา
ใช้เพื่อ: การค้นหาที่มีประสิทธิภาพ การเรียงลำดับข้อมูล การค้นหาข้อมูลภายในช่วง

ภาพจาก: https://www.geeksforgeeks.org/introduction-to-binary-search-tree-data-structure-and-algorithm-tutorials/

3. ต้นไม้ AVL (AVL Tree)

ต้นไม้ค้นหาแบบทวิภาคที่ปรับสมดุลตัวเอง (self-balancing)
ความสูงระหว่างต้นไม้ย่อยทั้งสองฝั่งของแต่ละโหนด ต่างกันได้ไม่เกิน 1
ใช้เพื่อ: รับประกันความเร็วในการค้นหา การเพิ่ม และการลบข้อมูลแบบ logarithmic time

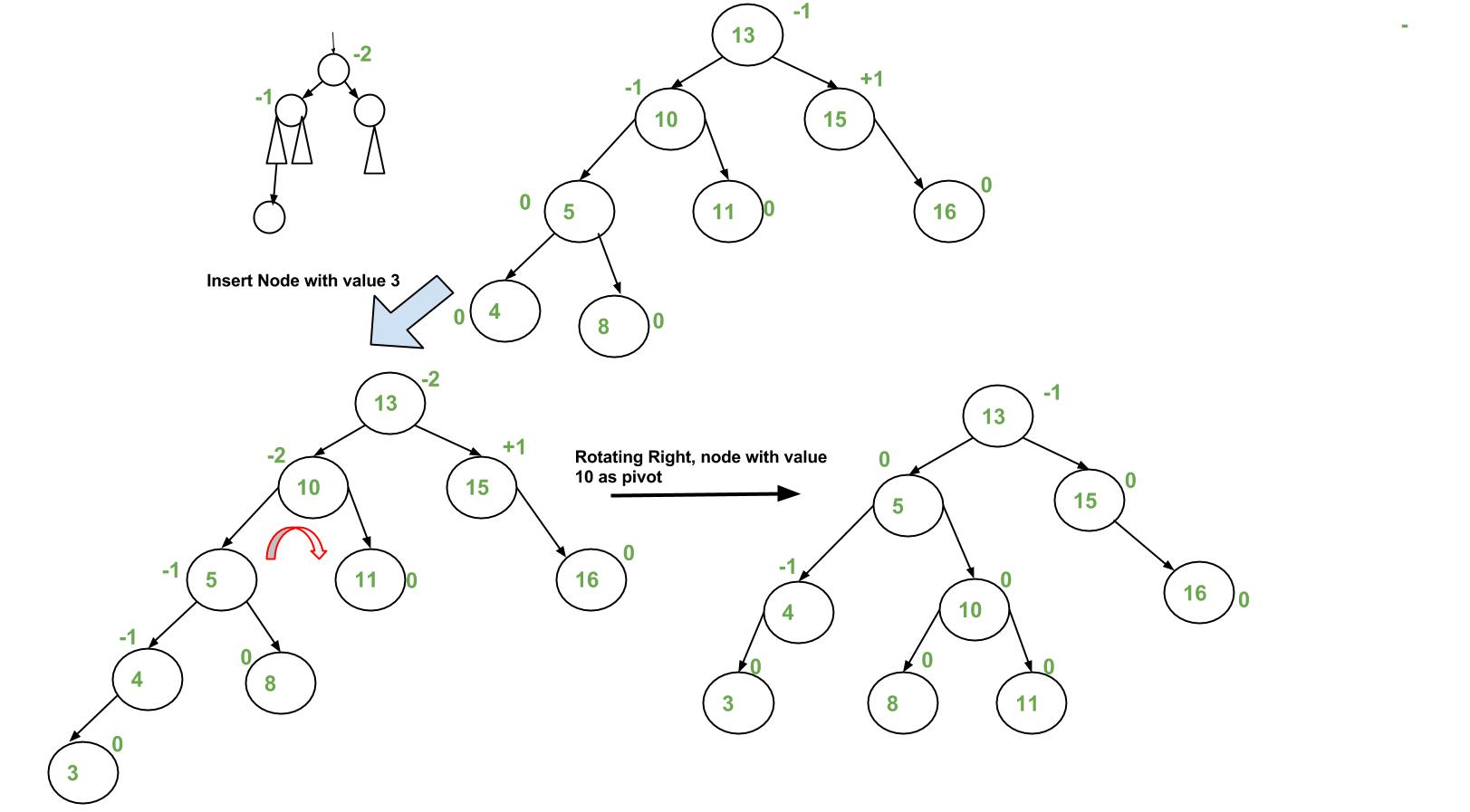
ภาพจาก: https://www.geeksforgeeks.org/insertion-in-an-avl-tree/

4. ต้นไม้แดงดำ (Red-Black Tree)

อีกหนึ่งต้นไม้ค้นหาแบบทวิภาคที่ปรับสมดุลตัวเอง (self-balancing)
ใช้คุณสมบัติ "สี" (แดงหรือดำ) ในการรักษาสมดุลของต้นไม้
ใช้เพื่อ: คล้ายกับ AVL Tree มักพบว่าถูกใช้ในการสร้างเซ็ต (set) และแมป (map) ในภาษาโปรแกรมต่างๆ

ภาพจาก: https://www.geeksforgeeks.org/introduction-to-red-black-tree/

5. ต้นไม้บี (B-Tree)

เป็นการต่อยอดจากต้นไม้ค้นหาแบบทวิภาคให้โหนดแต่ละตัวสามารถมีลูกได้มากกว่าสอง
นิยมใช้ในฐานข้อมูลและระบบไฟล์ (file system) เพื่อเพิ่มประสิทธิภาพการเข้าถึงข้อมูลบนดิสก์

ภาพจาก https://www.geeksforgeeks.org/introduction-of-b-tree-2/

6. ต้นไม้ไทร (Trie | Prefix Tree)

ต้นไม้ชนิดพิเศษสำหรับจัดเก็บข้อมูลประเภทข้อความ (string)
แต่ละเส้นทางภายในต้นไม้จะแทนคำหรือคำนำหน้าของคำ
ใช้เพื่อ: ระบบเติมคำอัตโนมัติ (autocomplete), การตรวจคำสะกด, การกำหนดเส้นทางของ IP (IP routing)

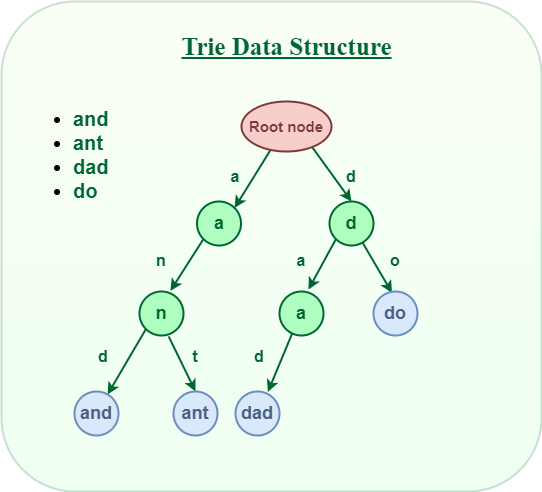
ภาพจาก https://www.geeksforgeeks.org/trie-insert-and-search/

ใน Tree พิเศษในแต่ละประเภท เราจะค่อยๆลงลึกกันในหัวข้อถัดๆไป

Tree คืออะไร​

Tree Representations in C++​

Basic Tree Code​

Tree Traversal​

Breadth-First Search (BFS)​

Depth-First Search (DFS)​

Tree Type​

Tree คืออะไร

Tree Representations in C++

Basic Tree Code

Tree Traversal

Breadth-First Search (BFS)

Depth-First Search (DFS)

Tree Type