Graph

Graph คืออะไร

• กราฟเป็นโครงสร้างข้อมูลแบบไม่เป็นเส้นตรง (non-linear) ประกอบด้วยโหนด (หรืออาจเรียกว่าจุดยอด) และเส้นเชื่อม (edges) เส้นเชื่อมจะเชื่อมต่อโหนดแต่ละคู่เข้าด้วยกัน เพื่อแสดงถึงความสัมพันธ์ระหว่างโหนดเหล่านั้น
• ประเภทของกราฟ:
  • กราฟมีทิศทาง (Directed Graph): เส้นเชื่อมมีทิศทางที่ชัดเจน แสดงถึงความสัมพันธ์แบบทางเดียว
  • กราฟไม่มีทิศทาง (Undirected Graph): เส้นเชื่อมเป็นแบบสองทาง บ่งบอกถึงความสัมพันธ์ที่เกิดขึ้นทั้งสองฝั่ง
  • กราฟมีน้ำหนัก (Weighted Graph): เส้นเชื่อมจะมีค่าหรือต้นทุนที่เกี่ยวข้อง เช่น อาจจะเป็นตัวแทนของระยะทาง หรือความจุ เป็นต้น

Main Concepts of a Graph

มีสองวิธีหลักๆ ในการจำลองกราฟด้วยภาษา C++:

1. Adjacency Matrix (เมทริกซ์แสดงความสัมพันธ์):

• ใช้ตารางสองมิติ (เมทริกซ์) โดยที่แถวและคอลัมน์จะแทนโหนดต่างๆ ในกราฟ
• หากมีเส้นเชื่อมระหว่างโหนด i และโหนด j ค่าของตำแหน่ง [i][j] ในเมทริกซ์จะมีค่า (มักจะใช้ค่า 1 สำหรับกราฟไม่มีน้ำหนัก หรือจะใส่ค่าน้ำหนักของเส้นเชื่อมลงไปสำหรับกราฟมีน้ำหนัก)
• ข้อดี: ตรวจสอบได้ง่ายว่ามีเส้นเชื่อมระหว่างสองโหนดหรือไม่
• ข้อเสีย: กินพื้นที่มากสำหรับกราฟเบาบาง (sparse graph) ซึ่งหมายถึงกราฟที่มีเส้นเชื่อมน้อยเมื่อเทียบกับจำนวนโหนด

#include <iostream>
#include <vector>

using namespace std;

class Graph {
public:
  int numVertices;
  vector<vector<int>> adjMatrix;
  bool directed = true; // Add a flag to indicate if the graph is directed

  Graph(int V) : numVertices(V), adjMatrix(V, vector<int>(V, 0)) {}

  void addEdge(int src, int dest) {
    adjMatrix[src][dest] = 1; // 1 for an unweighted graph
    if (!directed) {          // Add edge in reverse for undirected graphs
      adjMatrix[dest][src] = 1;
    }
  }

  void visualize() {
    // Print column headers (vertex numbers)
    cout << "   ";
    for (int i = 0; i < numVertices; i++) {
      cout << i << "  ";
    }
    cout << endl;

    // Print matrix with row labels
    for (int i = 0; i < numVertices; i++) {
      cout << i << ": ";
      for (int j = 0; j < numVertices; j++) {
        cout << adjMatrix[i][j] << "  ";
      }
      cout << endl;
    }
  }
};

int main() {
  Graph graph(5); // Graph with 5 vertices

  graph.addEdge(0, 1);
  graph.addEdge(0, 4);
  graph.addEdge(1, 2);
  graph.addEdge(1, 3);
  graph.addEdge(1, 4);
  graph.addEdge(2, 3);
  graph.addEdge(3, 4);

  cout << "Adjacency Matrix Representation:\n";
  graph.visualize();

  return 0;
}

คำอธิบาย

1. Graph Class:
   • numVertices: เก็บจำนวนจุดยอด (vertices) ทั้งหมดในกราฟ
   • adjMatrix: เป็นเวกเตอร์ (vector) สองมิติที่ใช้แทนเมทริกซ์แสดงความสัมพันธ์ (adjacency matrix)
2. addEdge(src, dest):
   • ฟังก์ชันนี้จะตั้งค่าที่เหมาะสมใน adjacency matrix เป็น 1 (หรือเป็นค่าน้ำหนักของเส้นเชื่อมสำหรับกรณีที่เป็นกราฟมีน้ำหนัก) เพื่อระบุว่ามีเส้นเชื่อมระหว่างโหนดต้นทาง (src) และโหนดปลายทาง (dest)
3. visualize():
   • ฟังก์ชันนี้จะพิมพ์ค่าใน adjacency matrix ออกมาในรูปแบบที่อ่านง่าย เพื่อให้เห็นภาพรวมได้ชัดเจนว่าโหนดใดเชื่อมต่อกับโหนดใดบ้าง

ตัวอย่างการเก็บ

Adjacency Matrix Representation:
   0  1  2  3  4  
0: 0  1  0  0  1  
1: 1  0  1  1  1  
2: 0  1  0  1  0  
3: 0  1  1  0  1  
4: 1  1  0  1  0

หน้าตา Graph

2. Adjacency List (รายการแสดงความสัมพันธ์):

• ใช้โครงสร้างข้อมูลแบบอาร์เรย์ (array) ที่มีรายการ (list หรือ vector) อยู่ภายในอีกชั้นนึง โดยแต่ละช่องในอาร์เรย์จะแทนโหนดหนึ่งๆ และรายการภายในช่องนั้นจะเก็บโหนดอื่นๆ ที่เชื่อมต่อถึงกัน
• ข้อดี: ประหยัดพื้นที่สำหรับกราฟแบบเบาบาง (sparse graphs)
• ข้อเสีย: จะตรวจสอบได้ช้ากว่า adjacency matrix ว่ามีเส้นเชื่อมระหว่างสองโหนดหรือไม่

#include <iostream>
#include <list>
#include <vector>

using namespace std;

// Node for the adjacency list
struct Node {
  int dest;
  int weight; // For weighted graphs

  Node(int d, int w = 1) : dest(d), weight(w) {}
};

class Graph {
public:
  int numVertices;
  vector<list<Node>> adjList;
  bool directed = false;

  Graph(int V) : numVertices(V), adjList(V) {}

  void addEdge(int src, int dest, int weight = 1) {
    adjList[src].push_back(Node(dest, weight));
    if (!directed) { // Add edge in reverse for undirected graphs
      adjList[dest].push_back(Node(src, weight));
    }
  }

  void visualize() {
    for (int i = 0; i < numVertices; i++) {
      cout << "Vertex " << i << ": ";
      for (Node node : adjList[i]) {
        cout << node.dest << "(" << node.weight << ") ";
      }
      cout << endl;
    }
  }
};

int main() {
  Graph graph(5); // Graph with 5 vertices

  graph.addEdge(0, 1);
  graph.addEdge(0, 4);
  graph.addEdge(1, 2);
  graph.addEdge(1, 3);
  graph.addEdge(1, 4);
  graph.addEdge(2, 3);
  graph.addEdge(3, 4);

  cout << "Adjacency List Representation:\n";
  graph.visualize();

  return 0;
}

คำอธิบาย

• Node: โครงสร้างข้อมูล (struct) ที่ใช้เก็บข้อมูลจุดหมายปลายของเส้นเชื่อม และอาจมีการเก็บค่าน้ำหนักของเส้นเชื่อมนั้นๆ ไว้ด้วย (สำหรับกรณีที่เป็นกราฟมีน้ำหนัก)
• Graph Class
  • numVertices: เก็บจำนวนจุดยอด (vertices) ทั้งหมดในกราฟ
  • adjList: เป็นเวกเตอร์ (vector) ที่เก็บรายการ (list) อยู่ภายในอีกที โดยแต่ละช่องในเวกเตอร์จะแทนโหนดหนึ่งๆ และรายการภายในช่องนั้นจะเก็บโหนดที่เชื่อมต่อกับโหนดนั้นๆ (และอาจเก็บค่าน้ำหนักของการเชื่อมต่อนั้นด้วย ถ้ามี)
• addEdge(): ฟังก์ชันนี้จะเพิ่มเส้นเชื่อมด้วยการเพิ่มข้อมูลของ 'Node' เข้าไปในรายการที่เหมาะสมภายใน adjList
• visualize(): ฟังก์ชันนี้จะไล่ดูข้อมูลใน adjList และพิมพ์การเชื่อมต่อของแต่ละโหนดออกมาให้อ่านง่าย

ตัวอย่างการเก็บ

Adjacency List Representation:
Vertex 0: 1(1) 4(1) 
Vertex 1: 0(1) 2(1) 3(1) 4(1) 
Vertex 2: 1(1) 3(1) 
Vertex 3: 1(1) 2(1) 4(1) 
Vertex 4: 0(1) 1(1) 3(1) 

เพื่อให้เกิดความเคยชิน เราจะใช้แบบ List แทน

Graph Traversal

Breadth-First Search (BFS)

• ประเภทของการสำรวจกราฟ (Traversal Technique): BFS ย่อมาจาก Breadth-first Search เป็นหนึ่งในอัลกอริทึมพื้นฐานสำหรับการสำรวจกราฟ โดยจะสำรวจ "ตามความกว้าง" ของกราฟก่อน ค่อยๆ ไล่ลงไปทีละระดับ เริ่มจากสำรวจโหนดที่อยู่ใกล้กับโหนดรากก่อน แล้วจึงค่อยไปยังโหนดที่อยู่ห่างออกไป
• วิธีการทำงาน:

1. เริ่มต้นที่โหนดต้นทาง: ทำเครื่องหมายว่าโหนดนี้ถูกเยี่ยมชมแล้ว
2. คิว (Queue): เพิ่มโหนดต้นทางนี้ลงไปในคิว
3. ทำซ้ำ (Iterate): ตราบใดที่คิวยังไม่ว่าง ให้ทำดังนี้...
   • นำโหนดตัวแรกสุดของคิวออก ("dequeue")
   • สำหรับแต่ละโหนดที่เชื่อมต่อกับโหนดที่นำออกมา และยังไม่เคยถูกสำรวจ:
     • ทำเครื่องหมายว่าโหนดนี้ถูกเยี่ยมชมแล้ว
     • เพิ่มโหนดนี้ลงไปในคิว

• ลำดับการเยี่ยมชม: BFS จะไปเยี่ยมชมโหนดทุกตัวที่เชื่อมต่อกับโหนดปัจจุบันให้ครบก่อน แล้วจึงจะไปสำรวจโหนดอื่นที่อยู่ห่างออกไปอีกหนึ่งระดับ

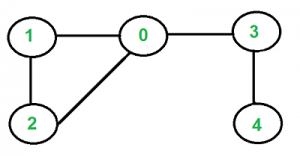
สมมุติว่าหน้าตากราฟแบบนี้

code

#include <iostream>
#include <queue>
#include <vector>
#include <list>

using namespace std;

// Node structure for the adjacency list
struct Node {
  int dest;
  int weight; // For weighted graphs

  Node(int d, int w = 1) : dest(d), weight(w) {}
};

class Graph {
public:
  int numVertices;
  vector<list<Node>> adjList;
  bool directed = false;

  Graph(int V) : numVertices(V), adjList(V) {}

  void addEdge(int src, int dest, int weight = 1) {
    adjList[src].push_back(Node(dest, weight));
    if (!directed) { // Add edge in reverse for undirected graphs
      adjList[dest].push_back(Node(src, weight));
    }
  }

  void bfs(int startVertex) {
    vector<bool> visited(numVertices, false);
    queue<int> q;

    visited[startVertex] = true;
    q.push(startVertex);

    while (!q.empty()) {
      int current = q.front();
      q.pop();

      cout << current << " "; // Process the node

      for (Node node : adjList[current]) {
        if (!visited[node.dest]) {
          visited[node.dest] = true;
          q.push(node.dest);
        }
      }
    }
  }
};

int main() {
  Graph graph(5); // Graph with 5 vertices

  // Add edges (modify as needed for your graph)
  graph.addEdge(0, 1);
  graph.addEdge(0, 4);
  graph.addEdge(1, 2);
  graph.addEdge(1, 3);
  graph.addEdge(1, 4);
  graph.addEdge(2, 3);
  graph.addEdge(3, 4);

  int startNode = 0;

  cout << "BFS Traversal starting from vertex " << startNode << ": ";
  graph.bfs(startNode);
  cout << endl;

  return 0;
}

คำอธิบาย

• visited: อาร์เรย์แบบบูลีน (boolean) เพื่อเก็บสถานะว่าโหนดต่างๆ ถูกสำรวจแล้วหรือยัง
• queue: โครงสร้างข้อมูลแบบคิว (queue) ใช้เพื่อจัดการลำดับการสำรวจโหนดต่างๆ
• bfs(graph, startVertex):
  • เริ่มต้นตั้งค่าในอาร์เรย์ visited
  • เพิ่ม startVertex ลงไปในคิว และทำเครื่องหมายว่าโหนดนี้ถูกสำรวจแล้ว
  • ตราบใดที่คิวไม่ว่าง ให้ทำซ้ำดังนี้:
    • นำโหนดตัวแรกสุดออกจากคิวและทำการประมวลผล (ในตัวอย่างคือการพิมพ์ออกมา)
    • เพิ่มโหนดทั้งหมดที่ยังไม่ถูกสำรวจและเชื่อมต่อกับโหนดนี้อยู่ลงไปในคิว และทำเครื่องหมายว่าโหนดเหล่านั้นถูกสำรวจแล้ว

ผลลัพธ์

BFS Traversal starting from vertex 0: 0 1 4 2 3

การประยุกต์ใช้ BFS

• เส้นทางที่สั้นที่สุด: ใช้ในการหาเส้นทางที่สั้นที่สุดระหว่างสองโหนดในกราฟไม่มีน้ำหนัก (unweighted graph)
• ระบบเครือข่ายแบบ Peer-to-Peer: ใช้ในการหา peer (โหนดอื่นๆ) ในระบบเครือข่าย P2P
• โปรแกรมช่วยค้นหาบนเว็บไซต์ (Web crawlers): ใช้เป็นพื้นฐานในการสร้าง web crawlers สำหรับทำดัชนี (index) ให้กับเว็บไซต์ต่างๆ
• การเก็บกวาดหน่วยความจำ (Garbage Collection): ระบบจัดการหน่วยความจำ (garbage collection) บางระบบก็ใช้แนวคิดที่คล้ายกันในการทำงาน

Depth-First Search (DFS)

• ประเภทของการสำรวจกราฟ (Traversal Technique): DFS ย่อมาจาก Depth-First Search เป็นอีกหนึ่งอัลกอริทึมสำคัญสำหรับการสำรวจกราฟ โดยจะเน้นการสำรวจลงไปใน "แนวลึก" ของกราฟให้ถึงที่สุดก่อน แล้วค่อยย้อนกลับมาสำรวจโหนดอื่นๆ ในภายหลัง
• วิธีการทำงาน:

1. เลือกโหนดต้นทาง: ทำเครื่องหมายว่าโหนดนี้ถูกเยี่ยมชมแล้ว
2. กระบวนการเรียกซ้ำ (Recursive process): สำหรับแต่ละโหนดที่เชื่อมต่อกับโหนดปัจจุบัน และยังไม่เคยถูกสำรวจ:
   • เรียกใช้ฟังก์ชัน DFS แบบเรียกซ้ำ โดยใส่โหนดที่เชื่อมต่อนั้นเป็นโหนดเริ่มต้น

• ลำดับการเยี่ยมชม: DFS จะสำรวจตามเส้นทางใดเส้นทางหนึ่งลงไปให้ลึกที่สุดเท่าที่จะทำได้ จนกระทั่งเจอโหนดที่ไม่มีโหนดใดเชื่อมต่ออยู่และยังไม่ถูกสำรวจ ค่อยย้อนกลับออกมา

สมมุติว่าหน้าตากราฟแบบเดียวกันกับ BFS

code

#include <iostream>
#include <queue>
#include <vector>
#include <list>

using namespace std;

// Node structure for the adjacency list
struct Node {
  int dest;
  int weight; // For weighted graphs

  Node(int d, int w = 1) : dest(d), weight(w) {}
};

class Graph {
public:
  int numVertices;
  vector<list<Node>> adjList;
  bool directed = false;

  Graph(int V) : numVertices(V), adjList(V) {}

  void addEdge(int src, int dest, int weight = 1) {
    adjList[src].push_back(Node(dest, weight));
    if (!directed) { // Add edge in reverse for undirected graphs
      adjList[dest].push_back(Node(src, weight));
    }
  }

  void dfsHelper(int vertex, vector<bool> &visited) {
    visited[vertex] = true;
    cout << vertex << " "; // Process the node

    for (Node node : adjList[vertex]) {
      if (!visited[node.dest]) {
        dfsHelper(node.dest, visited);
      }
    }
  }

  void dfs(int startVertex) {
    vector<bool> visited(numVertices, false);
    dfsHelper(startVertex, visited);
  }
};

int main() {
  Graph graph(5); // Graph with 5 vertices

  // Add edges (modify as needed for your graph)
  graph.addEdge(0, 1);
  graph.addEdge(0, 4);
  graph.addEdge(1, 2);
  graph.addEdge(1, 3);
  graph.addEdge(1, 4);
  graph.addEdge(2, 3);
  graph.addEdge(3, 4);

  int startNode = 0;

  cout << "DFS Traversal starting from vertex " << startNode << ": ";
  graph.dfs(startNode);
  cout << endl;

  return 0;
}

คำอธิบาย

• visited: อาร์เรย์แบบบูลีน (boolean) เพื่อเก็บสถานะว่าโหนดต่างๆ ถูกสำรวจแล้วหรือยัง
• dfsHelper(graph, vertex, visited):
  • ทำเครื่องหมายว่า vertex ปัจจุบันถูกเยี่ยมชมแล้ว
  • ประมวลผลโหนด (ในตัวอย่างนี้คือการพิมพ์ออกมา)
  • เรียกใช้ฟังก์ชัน dfsHelper แบบเรียกซ้ำ (recursively) กับโหนดทั้งหมดที่เชื่อมต่ออยู่และยังไม่เคยถูกสำรวจ
• dfs(graph, startVertex):
  • เริ่มต้นตั้งค่าในอาร์เรย์ 'visited'
  • เรียกฟังก์ชันแบบเรียกซ้ำ dfsHelper เพื่อเริ่มการสำรวจกราฟ

ผลลัพธ์

DFS Traversal starting from vertex 0: 0 1 2 3 4 

การประยุกต์ใช้การค้นหาเชิงลึก (DFS)

• การหาส่วนเชื่อมต่อกัน: ตรวจสอบว่ากราฟเชื่อมต่อทั้งหมดหรือระบุส่วนที่แยกจากกัน
• การจัดลำดับเชิงทอพอโลยี: การเรียงลำดับโหนดในกราฟแบบมีทิศทางตามการพึ่งพาอาศัยกัน
• การตรวจหา วัฏจักร (Cycles): ระบุว่าภายในกราฟมีวัฏจักรอยู่หรือไม่
• การแก้ปัญหาปริศนาและเขาวงกต: DFS มีบทบาทสำคัญในอัลกอริทึมสำหรับการแก้ปริศนาต่างๆ

ประเด็นสำคัญ

• โครงสร้างแบบเรียกซ้ำ (Recursive): DFS มีลักษณะเรียกซ้ำในตัว แตกต่างจาก BFS (การค้นหาเชิงกว้าง) ที่มักใช้คิว
• ลำดับการเยี่ยมชม: ลำดับที่ DFS เยี่ยมชมโหนดนั้นจะขึ้นอยู่กับลำดับการประมวลผลของโหนดข้างเคียงหรือโหนดลูก

Graph Type

1. กราฟไม่กำหนดทิศทาง (Undirected Graph)

• เส้นเชื่อมเป็นแบบสองทาง (ไม่มีแนวคิดของ "จาก" และ "ไปยัง") หากมีเส้นเชื่อมระหว่างโหนด A และ B แสดงว่าสามารถเดินทางได้ทั้งจาก A ไป B หรือจาก B ไป A

ภาพจาก: https://www.geeksforgeeks.org/what-is-unidrected-graph-undirected-graph-meaning/

2. กราฟกำหนดทิศทาง (Directed Graph)

• เส้นเชื่อมจะมีทิศทางที่กำหนดไว้ชัดเจน การที่มีเส้นเชื่อมจาก A ไป B ไม่ได้หมายความโดยอัตโนมัติว่าจะเดินทางจาก B กลับมายัง A ได้

ภาพจาก: https://www.geeksforgeeks.org/what-is-directed-graph-directed-graph-meaning/

3. กราฟมีน้ำหนัก (Weighted Graph)

• เส้นเชื่อมจะมีค่าน้ำหนักหรือค่าใช้จ่ายกำกับ ซึ่งอาจแสดงถึงปัจจัยต่างๆ เช่น ระยะทาง ความจุ หรือความแข็งแกร่งของความสัมพันธ์ระหว่างโหนด

ภาพจาก https://www.geeksforgeeks.org/in-a-weighted-graph-is-zero-allowed-as-an-edges-weight/

4. กราฟมีวัฏจักร (Cyclic Graph)

• กราฟที่มีอย่างน้อยหนึ่งวัฏจักร (เส้นทางที่เริ่มต้นและสิ้นสุดที่โหนดเดียวกัน)

ภาพจาก https://www.geeksforgeeks.org/what-is-cyclic-graph/

5. กราฟไร้วัฏจักร (Acyclic Graph)

• กราฟที่ไม่มีวัฏจักรเลย กราฟชนิดนี้มักจะมีลำดับหรือลำดับชั้นที่ชัดเจน

ภาพจาก https://www.geeksforgeeks.org/directed-acyclic-graph-in-compiler-design-with-examples/