Main Concept
วิธีการแก้ปัญหาด้วย DP
ในการแก้ปัญหาด้วย Dynamic Programming (DP) มีวิธีการหลัก 2 แนวทาง ได้แก่
- Memoization (Top-down approach)
- เป็นการเขียนฟังก์ชันแบบ recursive เพื่อแก้ปัญหาย่อยๆ และเก็บคำตอบของปัญหาย่อยไว้ใน memory เพื่อไม่ต้องคำนวณซ้ำ
- เริ่มจากปัญหาใหญ่ แล้วแตกเป็นปัญหาย่อยๆ ลงไปเรื่อยๆ จนถึงปัญหาย่อยที่เล็กที่สุด (base case)
- ก่อนจะเรียกฟังก์ชัน recursive ให้ตรวจสอบก่อนว่าเคยแก้ปัญหาย่อยนี้แล้วหรือยัง ถ้าเคยแล้วให้ดึงคำตอบจาก memory แทนการคำนวณใหม่
- ข้อดีคือเขียนโค้ดได้ง่าย เพราะคล้ายกับฟังก์ชัน recursive ปกติ แต่ข้อเสียคือใช้ memory เยอะ และอาจช้ากว่าแบบ tabulation
- Tabulation (Bottom-up approach)
- เป็นการสร้างตารางเพื่อเก็บคำตอบของปัญหาย่อยทั้งหมด โดยเริ่มจากป��ัญหาย่อยที่เล็กที่สุดไปจนถึงปัญหาใหญ่
- แก้ปัญหาย่อยทีละขั้นตอน และเก็บคำตอบลงในตาราง เพื่อนำไปใช้แก้ปัญหาที่ใหญ่ขึ้นในลำดับถัดไป
- ไม่จำเป็นต้องใช้ recursive function แต่ใช้ loop ในการแก้ปัญหาแทน
- ข้อดีคือใช้ memory น้อยกว่า และมีประสิทธิภาพดีกว่าแบบ memoization แต่ข้อเสียคือเขียนโค้ดยากกว่า เพราะต้องคิดลำดับการแก้ปัญหาให้ดี
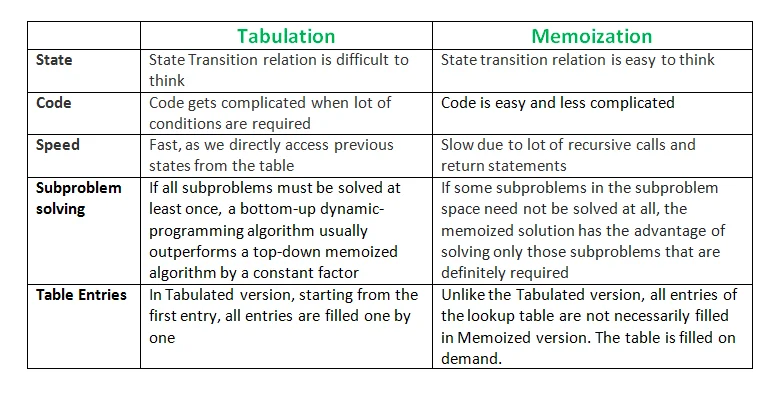
Ref: https://www.geeksforgeeks.org/tabulation-vs-memoization/
เราจะมาเล่าผ่านปัญหาสุด Classic นั่นคือ Fibonacci กัน
ปัญหา Fibonacci คือการหาลำดับ Fibonacci ซึ่งเป็นลำดับของจำนวนที่เริ่มต้นด้วย 0 และ 1 โดยที่แต่ละจำนวนถัดไปจะเท่ากับผลรวมของสองจำนวนก่อนหน้า
ลำดับ Fibonacci เริ่มต้นดังนี้
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
ซึ่ง สูตรเรียกซ้ำ (Recurrence relation) ของลำดับ Fibonacci (ที่เราเคยพูดถึงใน Recursive กันด้วย) คือ
F(0) = 0
F(1) = 1
F(n) = F(n-1) + F(n-2) สำหรับ n > 1
นี่คือโค้ด C++ สำหรับแก้ปัญหา Fibonacci โดยใช้สูตรเรียกซ้ำ (Recurrence relation)
#include <iostream>
using namespace std;
int fibonacci(int n) {
if (n <= 1) {
return n;
}
return fibonacci(n - 1) + fibonacci(n - 2);
}
int main() {
int n;
cout << "ป้อนตำแหน่งของจำนวน Fibonacci ที่ต้องการ: ";
cin >> n;
cout << "จำนวน Fibonacci ตำแหน่งที่ " << n << " คือ: " << fibonacci(n) << endl;
return 0;
}
โค้ดนี้ใช้วิธีการเรียกซ้ำโดยตรงตามสูตร Fibonacci ซึ่งมีข้อเสียคือ มีการคำนวณซ้ำกันเป็นจำนวนมาก ทำให้เกิดปัญหา Overlapping Subproblems แ��ละมีความซับซ้อนแบบ Exponential Time Complexity (O(2^n))
ดังนั้น เมื่อ n มีค่ามาก การคำนวณจะใช้เวลานานมาก วิธีการนี้จึงไม่เหมาะสมสำหรับ n ที่มีขนาดใหญ่ การแก้ปัญหานี้สามารถทำได้โดยใช้เทคนิค Dynamic Programming เช่น Tabulation หรือ Memoization เพื่อลดการคำนวณซ้ำและเพิ่มประสิทธิภาพในการหาคำตอบ
เราจะมาลองดูไอเดียของแต่ละวิธีผ่านตัวอย่าง Fibonacci กัน
Memoization
Memoization เป็นวิธีการแบบ Top-down เริ่มจากปัญหาใหญ่ แล้วแตกเป็นปัญหาย่อยลงไปเรื่อยๆ จนถึงปัญหาพื้นฐานที่เล็กที่สุด
- ใช้ Recursion ในการแก้ปัญหา แต่เก็บคำตอบของปัญหาย่อยที่เคยคำนวณแล้วไว้ใน Memo (ตารางหรืออาร์เรย์) เพื่อไม่ให้ต้องคำนวณซ้ำ
- เมื่อเจอปัญหาย่อยที่เคยคำนวณมาแล้ว จะนำคำตอบจาก Memo มาใช้เลย ไม่คำนวณใหม่
- เหมาะสำหรับกรณีที่ไม่จำเป็นต้องแก้ปัญหาย่อยทุกปัญหา แต่ต้องการแค่คำตอบสุดท้าย
และนี่คือ code ตัวอย่างของการใช้ Memoization
#include <iostream>
#include <vector>
using namespace std;
int fib(int n, vector<int> &memo) {
if (n <= 1)
return n;
if (memo[n] != -1)
return memo[n];
memo[n] = fib(n - 1, memo) + fib(n - 2, memo);
return memo[n];
}
int main() {
int n = 10;
vector<int> memo(n + 1, -1);
cout << fib(n, memo) << endl;
return 0;
}
อธิบาย code Memoization
- function
fibรับค่าnและmemoเป็น reference ของ vector ที่ใช้เก็บคำตอบของ sub problem ที่เคยคำนวณแล้ว - ถ้า
n <= 1คืนค่าnเลย เพราะเป็น base case - ถ้า
memo[n] != -1แสดงว่าเคยคำนวณค่านี้แล้ว ให้คืนค่าmemo[n]เลย ไม่ต้องคำนวณซ้ำ - ถ้ายังไม่เคยคำนวณ ให้เรียกเรียกฟังก์ชันแบบเรียกซ้ำ
fib(n-1, memo)และfib(n-2, memo)แล้วนำผลรวมมาเก็บในmemo[n] - คืนค่า
memo[n]เป็นคำตอบสุดท้าย - ในฟังก์ชัน
mainสร้าง vectormemoขนาดn+1และกำหนดค่าเริ่มต้นเป็น -1 เพื่อเช็คว่ายังไม่เคยคำนวณค่านั้นมาก่อน จากนั้นเรียกฟังก์ชันfib(n, memo)และแสดงผลลัพธ์
Tabulation
Tabulation เป็นวิธีการแบบ Bottom-up เริ่มจากแก้ปัญหาย่อยที่เล็กที่สุดก่อน แล้วค่อยๆ สร้างคำตอบของปัญหาใหญ่ขึ้นมาจากคำตอบของปัญหาย่อย
- เก็บคำตอบของปัญหาย่อยไว้ในตารางหรืออาร์เรย์ เพื่อใช้อ้างอิงในการแก้ปัญหาใหญ่ขึ้นไป
- มักใช้การวนลูปแบบ Iterative ในการแก้ปัญหา
- เหมาะสำหรับกรณีที่ต้องการคำตอบของปัญหาย่อยทุกปัญหา
#include <iostream>
#include <vector>
using namespace std;
int fib(int n) {
vector<int> dp(n + 1);
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
int main() {
int n = 10;
cout << fib(n) << endl;
return 0;
}
อธิบายโค้ด Tabulation
-
สร้างตาราง
dpขนาดn+1เพื่อเก็บคำตอบของปัญหาย่อย -
กำหนดค่าเริ่มต้นของ
dp = 0และdp = 1ซึ่งเป็นเคสฐาน -
ใช้ลูป
forเพื่อคำนวณค่า Fibonacci ตั้งแต่dp[1]ถึงdp[n]โดยใช้สูตรdp[i] = dp[i-1] + dp[i-2] -
สุดท้ายคืนค่า
dp[n]ซึ่งเป็นคำตอบของ Fibonacci ตัวที่ n
ความแตกต่างและการพิจารณาใช้
ความแตกต่างระหว่าง Tabulation และ Memoization ในการโปรแกรมแบบไดนามิก (Dynamic Programming)
Tabulation (Bottom-up)
- เป็นวิธีแบบ Bottom-up เริ่มจากแก้ปัญหาย่อยที่เล็กที่สุดก่อน แล้วค่อยๆ สร้างคำตอบของปัญหาใหญ่ขึ้นมาจากคำตอบของปัญหาย่อย
- ใช้ตารางหรืออาร์เรย์ในการเก็บคำตอบของปัญหาย่อยทั้งหมด
- มักใช้การวนล�ูปแบบ Iterative ในการแก้ปัญหา
- เหมาะสำหรับกรณีที่ต้องการคำตอบของปัญหาย่อยทุกปัญหา หรือมีจำนวน Input ที่มาก
Memoization (Top-down)
- เป็นวิธีแบบ Top-down เริ่มจากปัญหาใหญ่ แล้วแตกเป็นปัญหาย่อยลงไปเรื่อยๆ จนถึงปัญหาพื้นฐานที่เล็กที่สุด
- ใช้ Recursion ในการแก้ปัญหา แต่เก็บคำตอบของปัญหาย่อยที่เคยคำนวณแล้วไว้ใน Memo (ตารางหรืออาร์เรย์) เพื่อไม่ให้ต้องคำนวณซ้ำ
- เมื่อเจอปัญหาย่อยที่เคยคำนวณมาแล้ว จะดึงคำตอบจาก Memo แทนการคำนวณใหม่
- เหมาะสำหรับกรณีที่ไม่จำเป็นต้องแก้ปัญหาย่อยทุกปัญหา แต่ต้องการแค่คำตอบสุดท้าย หรือมีจำนวน Input ที่ไม่มากนัก
การเลือกใช้ Tabulation หรือ Memoization ขึ้นอยู่กับลักษณะของปัญหาและความต้องการ
- ถ้าต้องการคำตอบของปัญหาย่อยทุกปัญหา หรือมี Input ขนาดใหญ่ ควรใช้ Tabulation เพื่อหลีกเลี่ยงปัญหา Stack Overflow จากการเรียก Recursion มากเกินไป
- ถ้าต้องก�ารแค่คำตอบสุดท้าย หรือมี Input ขนาดเล็ก สามารถใช้ Memoization ได้ เพราะง่ายต่อการเขียนโค้ดและทำความเข้าใจ
- Tabulation มักจะเร็วกว่าและใช้หน่วยความจำน้อยกว่า Memoization เพราะไม่มี Overhead จากการเรียก Recursion
สรุปคือ ทั้ง Tabulation และ Memoization ต่างก็เป็นเทคนิคที่ช่วยเพิ่มประสิทธิภาพของ Dynamic Programming โดยลดการคำนวณซ้ำซ้อน แต่มีความแตกต่างกันในแง่ของวิธีการเก็บคำตอบย่อย ลักษณะการทำงาน และความเหมาะสมในการประยุกต์ใช้งาน
เพิ่มเติม สำหรับใครที่อยากขยี้เรื่องนี้เพิ่มเติม สามารถดูได้ในหัวข้อเก่าของช่องเราได้เช่นกัน
https://www.youtube.com/watch?v=A-kR-gIJxuw