Classic DP

ปัญหาในนี้จะถือเป็นปัญหา Classic ของ Dynamic programming ที่เราจะใช้วิธีการของ DP (ที่เรียนไปก่อนหน้า) ในการแก้ปัญหากัน

Coin Change

Ref: https://leetcode.com/problems/coin-change/description/
โจทย์: เราได้รับ Array ของเหรียญที่มีค่าต่างๆ (coins) และจำนวนเงินทั้งหมด (amount) เป้าหมายคือการหาจำนวนเหรียญน้อยที่สุดที่รวมกันแล้วเท่ากับจำนวนเงินที่ต้องการ ถ้าไม่สามารถหาจำนวนเหรียญใดๆ ที่รวมกันได้เท่ากับจำนวนเงินนั้น ให้คืนค่า -1
สำหรับการแก้ปัญหา Coin Change ด้วย Dynamic Programming เราสามารถใช้ทั้งวิธี Memoization (Top-down) และ Tabulation (Bottom-up) ได้ดังนี้

Tabulation (Bottom-up)

สร้างอาร์เรย์ dp ขนาด amount+1 เพื่อเก็บจำนวนเหรียญน้อยที่สุดสำหรับแต่ละจำนวนเงิน
กำหนดค่าเริ่มต้นของ dp = 0 เพราะต้องใช้ 0 เหรียญในการสร้างจำนวนเงิน 0
วนลูปจาก i = 1 ถึง amount เพื่ออัปเดตค่าใน dp:

กำหนด dp[i] = amount+1 เพื่อเป็นค่าเริ่มต้น
วนลูปเหรียญแต่ละเหรียญ ถ้า coin <= i อัปเดต dp[i] = min(dp[i], 1 + dp[i-coin])

ถ้า dp[amount] > amount แสดงว่าไม่มีคำตอบ คืนค่า -1 นอกนั้นคืนค่า dp[amount]
โค้ด C++ สำหรับ Tabulation

class Solution {
public:
  int coinChange(vector<int> &coins, int amount) {
    int n = coins.size();
    vector<int> dp(amount + 1, amount + 1);
    dp[0] = 0;

    for (int i = 1; i <= amount; i++) {
      for (int coin : coins) {
        if (coin <= i) {
          dp[i] = min(dp[i], 1 + dp[i - coin]);
        }
      }
    }

    return dp[amount] > amount ? -1 : dp[amount];
  }
};

Memoization (Top-down)

ฟังก์ชัน coinChange รับพารามิเตอร์ coins ซึ่งเป็นอาร์เรย์ของเหรียญ และ amount ซึ่งเป็นจำนวนเงินเป้าหมาย
สร้างอาร์เรย์ dp ขนาด amount+1 เพื่อเก็บผลลัพธ์ย่อยสำหรับแต่ละจำนวนเงิน โดยกำหนดค่าเริ่มต้นเป็น 0 เพื่อแสดงว่ายังไม่ได้คำนวณค่าในตำแหน่งนั้น
ใช้ lambda function solve เพื่อแก้ปัญหาย่อย โดยรับ rem (จำนวนเงินที่เหลือ) เป็นพารามิเตอร์

ถ้า rem == 0 แสดงว่าไม่ต้องใช้เหรียญใดๆ จึงคืนค่า 0
ถ้า dp[rem] != 0 แสดงว่าเคยคำนวณค่าในตำแหน่งนั้นแล้ว จึงคืนค่า dp[rem]
กำหนดตัวแปร minCoins เป็น INT\_MAX เพื่อเก็บจำนวนเหรียญน้อยที่สุดในการสร้างจำนวนเงิน rem
วนลูปเหรียญแต่ละเหรียญ:
ถ้า rem >= coin แสดงว่าจำนวนเงินที่เหลือมากกว่าหรือเท่ากับค่าเหรียญ จึงเรียกใช้ solve(rem - coin) เพื่อหาจำนวนเหรียญที่เหลือ
ถ้าผลลัพธ์ย่อย (subProb) ไม่เท่ากับ -1 แสดงว่าสามารถหาคำตอบได้ จึงอัปเดต minCoins ด้วยค่าน้อยที่สุดระหว่างค่าปัจจุบันและ 1 + subProb
หลังจากวนลูปเหรียญทั้งหมดแล้ว ถ้า minCoins ยังเป็น INT\_MAX แสดงว่าไม่สามารถหาคำตอบได้ จึงกำหนด dp[rem] = -1 นอกนั้นกำหนด dp[rem] = minCoins
คืนค่า dp[rem]

เรียกใช้ solve(amount) เพื่อหาคำตอบสุดท้าย และคืนค่ากลับ

class Solution {
public:
  int coinChange(vector<int> &coins, int amount) {
    int n = coins.size();
    vector<int> dp(amount + 1, 0);

    function<int(int)> solve = [&](int rem) {
      if (rem == 0)
        return 0;
      if (dp[rem] != 0)
        return dp[rem];

      int minCoins = INT_MAX;
      for (int coin : coins) {
        if (rem >= coin) {
          int subProb = solve(rem - coin);
          if (subProb != -1) {
            minCoins = min(minCoins, 1 + subProb);
          }
        }
      }

      dp[rem] = (minCoins == INT_MAX) ? -1 : minCoins;
      return dp[rem];
    };

    return solve(amount);
  }
};

0-1 Knapsack problem

Ref: https://www.geeksforgeeks.org/0-1-knapsack-problem-dp-10/
ปัญหา 0-1 Knapsack คือปัญหาการหาค่าที่เหมาะสมที่สุดในการเลือกของใส่ลงในกระเป๋าที่มีขนาดจำกัด โดยมีเงื่อนไขว่า "ของแต่ละชิ้นจะใส่หรือไม่ใส่ลงไปทั้งชิ้นเท่านั้น ไม่สามารถแบ่งของได้" (0 คือไม่ใส่, 1 คือใส่ทั้งชิ้น)
เป้าหมายคือต้องการให้ได้ผลรวมของมูลค่าของที่ใส่ลงไปมากที่สุด โดยที่น้ำหนักรวมต้องไม่เกินขนาดของกระเป๋า

Memoization

การแก้ปัญหา 0-1 Knapsack ด้วย Dynamic Programming โดยใช้เทคนิค Memoization สามารถทำได้ดังนี้

เริ่มจากการเขียนฟังก์ชันเรียกซ้ำ (recursive function) ที่รับพารามิเตอร์ดังนี้

n: จำนวนของ
W: ขนาดของกระเป๋า
wt[]: น้ำหนักของแต่ละชิ้น
val[]: มูลค่าของแต่ละชิ้น

สร้าง array 2 มิติขนาด (n+1) x (W+1) เพื่อเก็บผลลัพธ์ย่อยที่คำนวณแล้ว โดยกำหนดค่าเริ่มต้นเป็น -1
ในฟังก์ชันเรียกซ้ำ ให้ตรวจสอบว่าผลลัพธ์ย่อยถูกคำนวณไว้แล้วหรือยัง ถ้ามีอยู่แล้วให้ส่งค่านั้นกลับทันที
ถ้ายังไม่มีผลลัพธ์ย่อย ให้คำนวณโดยพิจารณา 2 กรณี:

ถ้าน้ำหนักของชิ้นปัจจุบันมากกว่าขนาดกระเป๋าที่เหลือ จะไม่สามารถใส่ชิ้นนี้ลงไปได้ ให้เรียกฟังก์ชันเรียกซ้ำกับ n-1 ชิ้น
ถ้าใส่ชิ้นนี้ได้ ให้เลือกระหว่างการใส่หรือไม่ใส่ชิ้นนี้ โดยเลือกค่าที่มากกว่าระหว่าง:
ใส่ชิ้นนี้ (val[n-1]) บวกกับผลลัพธ์ย่อยของ n-1 ชิ้นที่เหลือพื้นที่ W-wt[n-1]
ไม่ใส่ชิ้นนี้ ใช้ผลลัพธ์ย่อยของ n-1 ชิ้นเดิม

เก็บผลลัพธ์ย่อยลงใน array ก่อนส่งค่ากลับ
และนี่คือ code ของ c++

#include <iostream>
#include <vector>
using namespace std;

int knapsackMemo(int n, int W, vector<int> &wt, vector<int> &val, vector<vector<int>> &memo) {
  if (memo[n][W] != -1) {
    return memo[n][W];
  }

  if (n == 0 || W == 0) {
    memo[n][W] = 0;
  } else if (wt[n - 1] > W) {
    memo[n][W] = knapsackMemo(n - 1, W, wt, val, memo);
  } else {
    memo[n][W] = max(val[n - 1] + knapsackMemo(n - 1, W - wt[n - 1], wt, val, memo), knapsackMemo(n - 1, W, wt, val, memo));
  }

  return memo[n][W];
}

int main() {
  vector<int> val = {60, 100, 120};
  vector<int> wt = {10, 20, 30};
  int W = 50;
  int n = val.size();

  vector<vector<int>> memo(n + 1, vector<int>(W + 1, -1));

  cout << knapsackMemo(n, W, wt, val, memo);

  return 0;
}

Tabulation

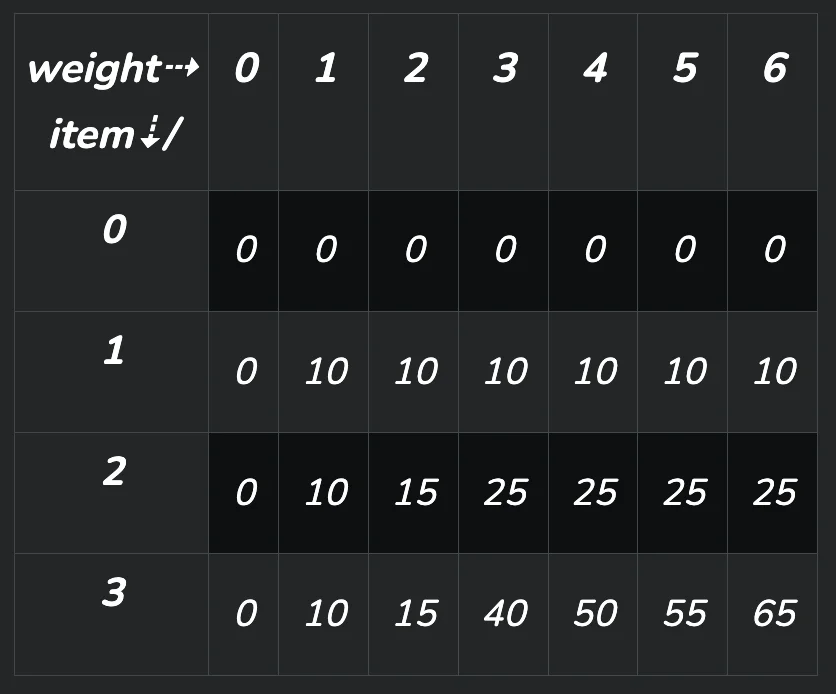
การแก้ปัญหา 0-1 Knapsack ด้วย Dynamic Programming โดยใช้เทคนิค Tabulation สามารถทำได้ดังนี้

สร้าง array 2 มิติ dp ขนาด (n+1) x (W+1) เพื่อเก็บค่าคำตอบย่อยของปัญหา โดย dp[i][w] จะเก็บมูลค่ารวมสูงสุดที่เป็นไปได้เมื่อพิจารณา i ไอเท็มแรกและน้ำหนักรวมไม่เกิน w
กำหนดค่าเริ่มต้นให้ dp[w] = 0 สำหรับทุก w ตั้งแต่ 0 ถึง W เนื่องจากเมื่อไม่มีไอเท็ม มูลค่าที่ใส่ได้จะเป็น 0
วนลูปตั้งแต่ i = 1 ถึง n เพื่อพิจารณาไอเท็มทีละตัว และวนลูปตั้งแต่ w = 0 ถึง W เพื่อพิจารณาน้ำหนักตั้งแต่ 0 ถึงความจุสูงสุดของกระเป๋า
สำหรับแต่ละค่า i และ w

ถ้าน้ำหนักของไอเท็มที่ i มากกว่า w ให้กำหนด dp[i][w] = dp[i-1][w] เพราะไม่สามารถใส่ไอเท็มนี้ลงในกระเป๋าได้
ถ้าน้ำหนักของไอเท็มที่ i น้อยกว่าหรือเท่ากับ w ให้กำหนด dp[i][w] = max(dp[i-1][w], val[i-1] + dp[i-1][w-wt[i-1]]) ซึ่งเลือกค่าที่มากกว่าระหว่างไม่ใส่ไอเท็มนี้กับใส่ไอเท็มนี้ลงไป

สุดท้าย คำตอบสูงสุดจะอยู่ที่ dp[n][W]
และนี่คือ code ของ c++

#include <algorithm>
#include <iostream>
using namespace std;

int knapSack(int W, int wt[], int val[], int n) {
  int i, w;
  int dp[n + 1][W + 1];

  for (i = 0; i <= n; i++) {
    for (w = 0; w <= W; w++) {
      if (i == 0 || w == 0)
        dp[i][w] = 0;
      else if (wt[i - 1] <= w)
        dp[i][w] = max(val[i - 1] + dp[i - 1][w - wt[i - 1]], dp[i - 1][w]);
      else
        dp[i][w] = dp[i - 1][w];
    }
  }

  return dp[n][W];
}

int main() {
  int val[] = {60, 100, 120};
  int wt[] = {10, 20, 30};
  int W = 50;
  int n = sizeof(val) / sizeof(val[0]);
  cout << knapSack(W, wt, val, n);
  return 0;
}

อย่างที่ทุกคนเห็น จะเห็นว่า ถ้าเราลองมองแบบตรงไปตรงมาจะเห็นว่า code แบบ "Tabulation" จะเขียน code สั้นกว่า แต่เบื้องหลังของไอเดียนั้น จะยากกว่า (สั้นแต่ยาก)
ปัญหาต่อจากนี้ เราอาจจะหยิบมาเพียง 1 ใน 2 วิธีนี้ โดยจะเลือกวิธีที่แก้ปัญหาได้ "สั้นกว่า" เป็นหลักนะครับ

Longest common subsequence

Ref: https://leetcode.com/problems/longest-common-subsequence/description/
กำหนด string text1 และ text2 ให้หาความยาวของ longest common subsequence ของสตริง (ลำดับของตัวอักษรที่ปรากฏใน string ต้นฉบับโดยเรียงลำดับเหมือนเดิม) แต่ไม่จำเป็นต้องติดกัน เช่น

"ace" เป็น subsequence ของ "abcde" ในขณะที่ "aec" ไม่ใช่

โดยวิธีแก้ปัญหาแบบ Dynamic programming คือ

สร้าง DP table ขนาด (m+1)*(n+1) เมื่อ m และ n คือความยาวของสตริง text1 และ text2 ตามลำดับ โดยเซลล์ dp[i][j] จะเก็บความยาว LCS ของ text1[0…i-1] และ text2[0…j-1]
กำหนดเงื่อนไขเริ่มต้น (base case) โดยเซลล์ในแถวแรกและคอลัมน์แรกของตาราง DP จะมีค่าเป็น 0 เนื่องจากถ้าสตริงใดสตริงหนึ่งว่าง LCS จะมีความยาวเป็น 0
วนลูปเพื่อกรอกค่าลงในตาราง DP

ถ้าตัวอักษรที่ตำแหน่ง i ใน text1 ตรงกับตัวอักษรที่ตำแหน่ง j ใน text2 (text1[i-1] == text2[j-1]) ให้กำหนดค่า dp[i][j] = dp[i-1][j-1] + 1
ถ้าตัวอักษรไม่ตรงกัน ให้กำหนดค่า dp[i][j] = max(dp[i-1][j], dp[i][j-1]) เพื่อเลือกค่า LCS ที่ยาวที่สุดระหว่างการตัดตัวอักษรตัวสุดท้ายของ text1 หรือ text2 ออก

เมื่อกรอกค่าในตาราง DP ครบแล้ว ค่าใน dp[m][n] จะเป็นความยาวของ Longest Common Subsequence ระหว่างสตริง text1 และ text2

ตัวอย่างโค้ด C++ ที่ใช้ Dynamic Programming เพื่อแก้ปัญหา LCS

class Solution {
public:
  int longestCommonSubsequence(string text1, string text2) {
    int m = text1.length(), n = text2.length();
    vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));

    for (int i = 1; i <= m; i++) {
      for (int j = 1; j <= n; j++) {
        if (text1[i - 1] == text2[j - 1])
          dp[i][j] = dp[i - 1][j - 1] + 1;
        else
          dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
      }
    }

    return dp[m][n];
  }
};

ผลลัพธ์ตาราง DP

    a b c d e
  0 0 0 0 0 0
a 0 1 1 1 1 1
c 0 1 1 2 2 2
e 0 1 1 2 2 3

ความซับซ้อนเชิงเวลาของวิธีนี้คือ O(mn) เนื่องจากต้องแก้ปัญหาย่อย mn ปัญหา ส่วนความซับซ้อนเชิงพื้นที่คือ O(mn) เพื่อเก็บตาราง DP ขนาด (m+1)(n+1)
สรุปคือ การใช้ Dynamic Programming ช่วยลดความซับซ้อนเชิงเวลาจาก O(2^(m+n)) ของวิธี Recursive ลงเหลือ O(mn) แต่ต้องแลกมาด้วยการใช้หน่วยความจำเพิ่มขึ้นเป็น O(mn) เพื่อสร้างตาราง memoization

Longest increasing subsequence

Ref: https://leetcode.com/problems/longest-increasing-subsequence/description/
ลำดับย่อยเพิ่มขึ้นที่ยาวที่สุด (Longest Increasing Subsequence หรือ LIS) คือลำดับย่อยของลำดับที่กำหนดให้ โดยที่องค์ประกอบทั้งหมดในลำดับย่อยนั้นเรียงลำดับจากน้อยไปมาก
ตัวอย่างเช่น ให้ลำดับ 80 LIS คือ 80 ซึ่งมีความยาว 6
วิธีแก้ปัญหา LIS ด้วย Dynamic Programming ในภาษา C++ มีขั้นตอนดังนี้

สร้าง array dp ขนาด n เพื่อเก็บความยาวของ LIS ที่ลงท้ายด้วยแต่ละ index โดยกำหนดค่าเริ่มต้นเป็น 1 ทั้งหมด
วนลูปตั้งแต่ index 0 ถึง n-1 เพื่อพิจารณาแต่ละตัวเลข

เปรียบเทียบตัวเลขปัจจุบันกับตัวเลขก่อนหน้าทุกตัว
ถ้าตัวเลขปัจจุบันมากกว่าตัวเลขก่อนหน้า ให้อัปเดต dp[i] เป็นค่ามากสุดระหว่าง dp[i] กับ dp[j]+1

หลังจบลูป ค่าที่มากที่สุดใน dp คือความยาวของ LIS

class Solution {
public:
  int lengthOfLIS(vector<int> &nums) {
    int n = nums.size();
    vector<int> dp(n, 1);

    for (int i = 0; i < n; i++) {
      for (int j = 0; j < i; j++) {
        if (nums[i] > nums[j]) {
          dp[i] = max(dp[i], dp[j] + 1);
        }
      }
    }

    return *max_element(dp.begin(), dp.end());
  }
};

ปัญหาอื่นๆ ใน Leet code แนะนำ

Target Sum 494

Ref: https://leetcode.com/problems/target-sum/description/

กำหนดอาร์เรย์ nums ที่เก็บตัวเลขจำนวนเต็ม และตัวเลขเป้าหมาย target ให้หาจำนวนวิธีทั้งหมดในการเพิ่มเครื่องหมาย + หรือ - ไว้ข้างหน้าตัวเลขแต่ละตัวใน nums เพื่อให้ผลรวมเท่ากับ target
วิธีแก้ปัญหาด้วย Dynamic Programming มีดังนี้

สร้างอาร์เรย์ dp ขนาด sum(nums)+1 เพื่อเก็บจำนวนวิธีที่ทำให้ได้ผลรวมตั้งแต่ 0 ถึง sum(nums)
กำหนดให้ dp = 1 เพราะมีวิธีเดียวที่จะได้ผลรวม 0 คือไม่เลือกตัวเลขใดเลย
วนลูปตัวเลขแต่ละตัวใน nums:

สำหรับแต่ละตัวเลข num ให้วนลูปย้อนหลังจาก j = target ถึง j >= num
อัปเดต dp[j] += dp[j-num] เพื่อเพิ่มจำนวนวิธีที่จะได้ผลรวม j โดยใช้ตัวเลข num

สุดท้าย dp[target] จะเก็บคำตอบ คือจำนวนวิธีทั้งหมดที่จะได้ผลรวมเท่ากับ target
ความซับซ้อนของอัลกอริทึมนี้คือ O(n*sum(nums)) โดย n คือจำนวนตัวเลขใน nums ซึ่งดีกว่าวิธี Brute Force ที่ต้องใช้เวลา O(2^n)

Dungeon Game 174

Ref: https://leetcode.com/problems/dungeon-game/description/

โจทย์ กำหนดตารางขนาด m x n แทนด่านในเกม โดยแต่ละช่องจะมีค่าพลังงาน (เลขจำนวนเต็ม) ให้ผู้เล่นเดินทางจากช่องซ้ายบนไปยังช่องขวาล่างของตาราง โดยเริ่มต้นที่ช่องซ้ายบนด้วยพลังงาน 1 หน่วย
เมื่อผู้เล่นเดินทางไปยังช่องใดๆ พลังงานจะเพิ่มหรือลดตามค่าในช่องนั้น ผู้เล่นจะเสียชีวิตทันทีถ้าพลังงานเหลือน้อยกว่าหรือเท่ากับ 0 จงหาค่าพลังงานเริ่มต้นน้อยที่สุดที่ผู้เล่นต้องมีเพื่อให้รอดชีวิตและไปถึงช่องขวาล่างได้
วิธีแก้ปัญหาด้วย Dynamic Programming มีดังนี้:

สร้างตาราง dp ขนาดเท่ากับตารางเดิม เพื่อเก็บค่าพลังงานน้อยที่สุดที่ต้องการเมื่อเดินทางมาถึงแต่ละช่อง
เริ่มจากช่องขวาล่าง dp[m-1][n-1] = max(1, 1-dungeon[m-1][n-1]) เพื่อให้มีพลังงานเหลืออย่างน้อย 1 หน่วยเมื่อถึงช่องสุดท้าย
วนลูปย้อนกลับไปยังช่องด้านซ้ายและด้านบน เพื่ออัปเดตค่า dp ตามสูตร:

dp[i][j] = max(1, min(dp[i+1][j], dp[i][j+1]) - dungeon[i][j])
เลือกเส้นทางที่ใช้พลังงานน้อยที่สุดระหว่างไปทางขวาหรือลง แล้วลบด้วยค่าในช่องปัจจุบัน

สุดท้าย dp จะเก็บคำตอบ คือพลังงานเริ่มต้นน้อยที่สุดที่ต้องการ
ความซับซ้อนของอัลกอริทึมนี้คือ O(mn) เนื่องจากต้องวนลูปทุกช่องในตาราง
** ปัญหาอื่นๆ เราจะเริ่มนำมาประยุกต์ใช้ในหัวข้อ Graph, Tree อีกที
อย่างที่ทุกคนเห็นว่า ปัญหา Dynamic programming แม้จะมีปัญหาหลากหลายรูปแบบก็จริง แต่ไอเดียการแก้ปัญหายังอยู่ภายใน 2 รูปแบบคือ Memorization และ Tabulation
ขอแค่ scope ปัญหาอยู่ภายใน Dynamic programming ก็สามารถที่ใช้วิธีแก้ปัญหาแบบ Dynamic programming ได้

Coin Change​

Tabulation (Bottom-up)​

Memoization (Top-down)​

0-1 Knapsack problem​

Memoization​

Tabulation​

Longest common subsequence​

Longest increasing subsequence​

ปัญหาอื่นๆ ใน Leet code แนะนำ​

Target Sum 494​

Dungeon Game 174​