NP Problem

ปัญหา P และ NP คืออะไร

จากหัวข้อก่อนหน้านี้ที่เราเรียนเรื่อง Code Complexity ไป เราจะเจอว่าบางปัญหาสามารถแก้ได้ไวมาก และบางปัญหาต้องใช้เวลาแก้นานมาก (เช่น Permutation) เราจะมาเข้าสู่ โลกของปัญหา P และ NP กัน เพื่อให้นิยามของปัญหาและประเภทของปัญหาที่เราจะแก้ชัดเจนยิ่งขึ้น

เรื่องราวของปัญหา P และ NP เป็นหนึ่งในปัญหาที่สำคัญที่สุดในทฤษฎีวิทยาการคำนวณ ซึ่งมีที่มาและคำนิยามดังนี้

ในปี 1936 นักคณิตศาสตร์ชาวอังกฤษ Alan Turing ได้นำเสนอแนวคิดของ "Turing Machine" ซึ่งเป็นรูปแบบทฤษฎีของเครื่องคอมพิวเตอร์ที่สามารถคำนวณได้ทุกอย่าง จากนั้นในปี 1971 นักวิทยาการคอมพิวเตอร์ชาวอเมริกัน Stephen cook ได้แบ่งประเภทของปัญหาคอมพิวเตอร์ออกเป็น 2 กลุ่มหลักๆ คือ

1. ปัญหา P (Polynomial Time) หมายถึงปัญหาที่สามารถแก้ได้ในเวลาที่เป็นพหุนามของขนาดของปัญหา นั่นคือมี algorithm ที่สามารถแก้ปัญหาได้ในเวลา O(n^k) สำหรับค่าคงที่ k บางค่าที่สามารถหาได้

ตัวอย่าง

• การค้นหาค่ามากที่สุดใน Array = O(n)
• การค้นหาเส้นทางสั้นที่สุดใน Graph ด้วย Dijkstra = O((V+E) log V) โดยที่ V คือจำนวนจุด และ E คือจำนวนเส้นเชื่อม (แม้จะไม่ได้เขียนอยู่ในรูป O(n^k) แต่ก็ยังคงอยู่ใน function พหุนาม เนื่องจากใน Graph ปกติ จำนวนเส้นเชื่อม E จะมีค่าไม่เกิน V(V-1)/2 ดังนั้น Complexity จึงอยู่ในระดับ O(V^2 log V) ซึ่งเป็นพหุนามออกมาได้)
• การคำนวณผลรวมของเลขคณิตระหว่าง 1 ถึง n = O(1) เนื่องจากใช้สูตรคณิตศาสตร์ n(n+1)/2 ในการคำนวณได้

2. ปัญหา NP (Non-deterministic Polynomial Time) หมายถึงปัญหาที่เมื่อให้คำตอบมา เราสามารถตรวจสอบความถูกต้องของคำตอบนั้นได้ในเวลาพหุนาม แต่ “ไม่มี algorithm ที่รู้จักในปัจจุบันที่สามารถแก้ปัญหาเหล่านี้ได้ในเวลาพหุนาม”

ตัวอย่าง

• ปัญหาการเดินทางของพนักงานขาย (Traveling Salesman Problem) = O(n!) เนื่องจากต้องพิจารณาเส้นทางทั้งหมด n! เส้นทาง
• ปัญหาการแก้เกม sudoku = O(9^(n^2)) เนื่องจากต้องพิจารณาการวางตัวเลข 1-9 ในช่องว่างทั้งหมด n^2 ช่อง
• ปัญหาการแยกตัวประกอบ (Integer Factorization) = O(2^n)

โดย คำนิยามของปัญหา P และ NP ที่มีการระบุเอาไว้นั้น

• ปัญหา P คือชุดของปัญหาที่สามารถแก้ได้ด้วย algorithm ที่มีเวลาทำงานเป็นพหุนามของขนาดของปัญหา (Polynomial Time) ซึ่งถือว่าเป็นปัญหาที่ "ง่าย" หรือ "สามารถแก้ได้อย่างมีประสิทธิภาพ"
• ปัญหา NP คือชุดของปัญหาที่เมื่อให้คำตอบมา เราสามารถตรวจสอบความถูกต้องของคำตอบนั้นได้ในเวลาพหุนาม แต่ยังไม่มี algorithm ที่รู้จักที่สามารถแก้ปัญหาเหล่านี้ได้ในเวลาพหุนาม ซึ่งถือว่าเป็นปัญหาที่ "ยาก"

แล้ว ทำไมปัญหา NP จึงมีความสำคัญ ปัญหา NP มีความสำคัญเนื่องจากเป็นปัญหาที่พบได้บ่อยในชีวิตจริงและมีประโยชน์ในหลายสาขา เช่น

1. ความปลอดภัยบนอินเทอร์เน็ต หลายระบบรักษาความปลอดภัยบนอินเทอร์เน็ตอาศัยปัญหา NP เช่น การแยกตัวประกอบของจำนวนเฉพาะขนาดใหญ่ ซึ่งเป็นพื้นฐานของการเข้ารหัส RSA
2. การวิจัยทางชีวภาพ การเข้าใจเส้นทางการ Protein folding และการค้นหาลำดับย่อยในลำดับ DNA ขนาดใหญ่ เป็นปัญหา NP ที่มีประโยชน์ในการศึกษาวิธีรักษาโรค
3. การจัดการและการวางแผน ปัญหาการจัดตารางการทำงาน การวางแผนการผลิต และการค้นหาเส้นทางการขนส่งที่ประหยัดที่สุด ล้วนเป็นปัญหา NP ที่มีประโยชน์ในการลดต้นทุนและเพิ่มประสิทธิภาพ
4. ทฤษฎีพื้นฐานทางคณิตศาสตร์ การศึกษาปัญหา NP ช่วยให้เราเข้าใจขีดจำกัดของการคำนวณและความซับซ้อนของ algorithm ได้ดียิ่งขึ้น

เพราะฉะนั้น ด้วยความสำคัญที่ส่งเสริมการแก้ปัญหาหลายๆอย่าง จึงได้เกิดความพยายามในการพิสูจน์ ปัญหา P = NP ออกมา

ปัญหา P = NP เป็นคำถามที่ยังไม่มีคำตอบว่า ปัญหาทุกปัญหาในกลุ่ม NP สามารถแก้ได้ในเวลาพหุนามหรือไม่ หากคำตอบคือ "ใช่" แสดงว่า P = NP ซึ่งสิ่งนี้จะส่งผลกระทบอย่างมากต่อวงการคอมพิวเตอร์และเทคโนโลยีสารสนเทศหากสามารถแก้ปัญหาได้

ถ้า P = NP จริง จะหมายความว่า

• ปัญหาที่ปัจจุบันถือว่ายากมาก เช่น Traveling Salesman จะสามารถแก้ได้อย่างรวดเร็ว (รวมถึงปัญหาอื่นๆที่อยู่ในตระกูลของ NP)
• ระบบรักษาความปลอดภัยบนอินเทอร์เน็ตจะถูกคุกคามอย่างรุนแรง (เพราะเราสามารถ solve NP ซึ่งเป็นปัญหาอย่างของเหล่า cryptography ได้)
• คอมพิวเตอร์จะสามารถค้นหาคำตอบที่ดีที่สุดสำหรับปัญหาการจัดตารางได้อย่างรวดเร็ว

แต่ถ้า P ≠ NP ซึ่งเป็นสิ่งที่นักวิทยาการคอมพิวเตอร์ส่วนใหญ่เชื่อ จะหมายความว่ายังคงมีปัญหาบางอย่างที่ไม่สามารถแก้ได้ด้วยวิธีการที่มีประสิทธิภาพ และยังคงทำให้ NP ยังคงเป็นปัญหายากเช่นเดิมนั่นเอง

** จริงๆถ้าจะให้เล่าอีกมุมหนึ่งคือ ในปัจจุบันเราได้ใช้ประโยชน์จากความยากของปัญหา NP ในหลายๆ ด้าน โดยเฉพาะอย่างยิ่งในด้านความปลอดภัยของข้อมูลและการเข้ารหัส ดังนั้น แม้ว่าปัญหา NP จะเป็นปัญหาที่ยากสำหรับการแก้ไข แต่ความยากนี้กลับกลายเป็นประโยชน์ในการสร้างระบบรักษาความปลอดภัยและความเป็นส่วนตัวต่างๆ ที่มีความสำคัญอย่างยิ่งในโลก Digital ปัจจุบันนี้นั่นเอง (ex. Zero-Knowledge Proofs, Cryptographic Hash Functions [SHA256], Cryptography [RSA])

NP Complete และ NP Hard

Ref: https://www.geeksforgeeks.org/introduction-to-np-completeness/

NP (Non-deterministic Polynomial time) เป็นกลุ่มของปัญหาที่เราสามารถตรวจสอบคำตอบได้ในเวลาพอลิโนเมียล แต่ยังไม่พบวิธีการหาคำตอบในเวลาพหุนาม

NP-Complete เป็นกลุ่มย่อยของ NP ที่ “ยากที่สุด” โดยปัญหาใด ๆ ใน NP สามารถถูกลดรูปมาเป็นปัญหา NP-Complete ได้ในเวลาพหุนาม หากเราสามารถแก้ปัญหา NP-Complete ได้ในเวลาพหุนามได้ เราก็จะสามารถแก้ปัญหาอื่น ๆ ใน NP ได้ด้วย

NP-Hard เป็นกลุ่มของปัญหาที่ “ยากไม่น้อยกว่าหรือยากกว่าปัญหา NP-Complete” โดยปัญหา NP-Complete สามารถถูกลดรูปเป็นปัญหา NP-Hard ได้ในเวลาพหุนาม

ก่อนจะไปมองภาพต่อ เราต้องรู้จักกับหลักการของการลดรูป (reducibility) กันก่อน

นิยามของการ “การลดรูป” (reduce) จากปัญหาหนึ่งไปยังอีกปัญหาหนึ่งในเวลาพหุนาม หมายความว่า เราสามารถเขียน algorithm ที่แปลงข้อมูล input ของปัญหาแรกไปเป็นข้อมูล input ของปัญหาที่สองได้ในเวลาพหุนาม (ตามทฤษฎีเราจะเรียกว่า Polynomial-time reducibility)

ตัวอย่างเช่น เราสามารถลดรูปปัญหา 3SAT ที่เป็น NP-Complete มายังปัญหาการค้นหา Hamiltonian cycle ได้ โดยสร้างกราฟจาก Boolean expression ของ 3SAT แล้วแสดงว่า expression นั้นเป็นจริงได้ ก็ต่อเมื่อกราฟที่สร้างขึ้นมี Hamiltonian cycle

ดังนั้น ถ้าเราสามารถแก้ปัญหา Hamiltonian cycle ได้ เราก็จะสามารถนำคำตอบนั้นมาแก้ปัญหา 3SAT ได้ด้วย เนื่องจากเราลดรูปจาก 3SAT มายังปัญหา Hamiltonian cycle ได้แล้วนั่นเอง

หลายคนก็จะเริ่มสงสัยและ “แล้วปัญหาแรกสุดของ NP Complete” ละ พิสูจน์จากอะไร ? การพิสูจน์ปัญหาแรกที่เป็น NP-Complete คือปัญหา Boolean Satisfiability (SAT) ซึ่งเป็นผลงานของ Stephen Cook และ Leonid Levin ในปี 1971

ปัญหา SAT คือการหาการกำหนดค่า true / false ให้กับตัวแปร boolean ต่างๆ เพื่อให้ Boolean expression ที่กำหนดมาเป็นจริง

ตัวอย่างเช่น จาก Boolean expression นี้ (x ∨ ¬y) ∧ (¬x ∨ z) ∧ (¬z ∨ y) โจทย์คือให้หาการกำหนดค่าจริง (true) หรือเท็จ (false) ให้กับตัวแปร x, y และ z เพื่อให้ Boolean expression ข้างต้นเป็นจริง

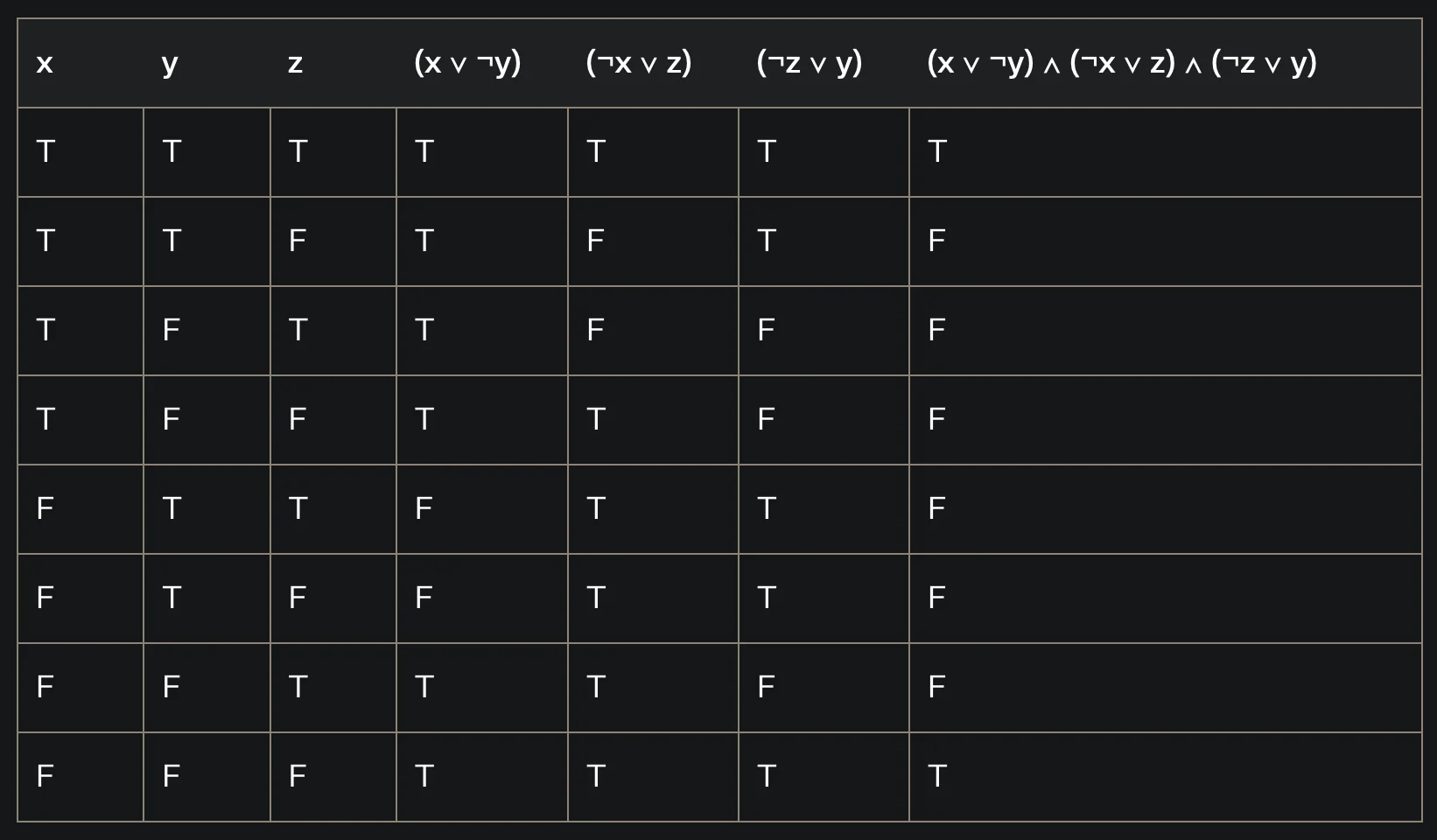
หากเราลองไปสร้างตารางค่าความจริงดู เราสามารถเห็นได้ว่ามีเพียงการกำหนดค่าเดียวที่ทำให้ expression เป็นจริง นั่นคือ x = F, y = F และ z = F ดังนั้น คำตอบของปัญหา SAT สำหรับ expression นี้คือ x = false, y = false, z = false

ขั้นตอนในการพิสูจน์ว่า SAT เป็น NP-Complete มีดังนี้

1. แสดงว่า SAT อยู่ในชั้น NP

   • ทดสอบใส่ข้อมูล SAT คือการกำหนดค่า true / false ให้กับตัวแปร
   • สามารถตรวจสอบได้ในเวลาพหุนามว่าการกำหนดค่านั้นทำให้ express เป็นจริงหรือไม่ (ตรงตามคุณสมบัตของ NP)

2. แสดงวิธีการลดรูปจากปัญหาอื่นๆ ในชั้น NP มายัง SAT ได้ในเวลาพหุนาม

   • Cook แสดงวิธีสร้าง expression SAT จากการทำงานของเครื่อง Non-deterministic Turing Machine (Non-deterministic Turing Machine เป็นแบบจำลองทางทฤษฎีของการคำนวณแบบไม่แน่นอน ซึ่งเป็นตัวแทนของปัญหาในชั้น NP)
   • Cook สร้าง expression SAT ที่มีตัวแปรแทนสถานะต่างๆ ของเครื่อง Non-deterministic Turing Machine
   • expression SAT ที่สร้างขึ้นจะเป็นจริงได้ก็ต่อเมื่อเครื่อง Non-deterministic Turing Machine นั้นยอมรับข้อมูลนำเข้า
   • ดังนั้น ถ้าสามารถแก้ SAT ได้ ก็จะสามารถแก้ปัญหาอื่นๆ ในชั้น NP ได้ด้วย โดยการลดรูปมาจากเครื่อง Non-deterministic Turing Machine นั่นเอง

3. แสดงว่าการลดรูปจากเครื่อง Non-deterministic Turing Machine มายัง SAT สามารถทำได้ในเวลาพหุนาม

• ขนาดของ expression SAT ที่สร้างขึ้นมีขนาดพอลิโนเมียลเมื่อเทียบกับขนาดของข้อมูลนำเข้าของ Non-deterministic Turing Machine
• การสร้างและประเมิน expression SAT สามารถทำได้ในเวลาพหุนาม

เนื่องจาก Non-deterministic Turing Machine เป็นแบบจำลองของปัญหาในชั้น NP การลดรูปจาก Non-deterministic Turing Machine มายัง SAT จึงเท่ากับการลดรูปจากปัญหาอื่นๆ ในชั้น NP มายัง SAT ได้ทั้งหมด ดังนั้น การพิสูจน์ของ Cook และ Levin จึงแสดงให้เห็นว่า SAT เป็นปัญหายากที่สุดในชั้น NP เนื่องจากปัญหาอื่นๆ ทั้งหมดในชั้นนี้สามารถลดรูปมาเป็น SAT ได้ทั้งหมด ทำให้ SAT เป็นปัญหา NP-Complete ปัญหาแรกออกมาได้นั่นเอง

นั่นจึงเป็นเหตุผลที่ว่าทำไมปัญหานี้จึง “ยากกว่า” เพราะ การลดรูปจากปัญหาอื่นๆ ใน NP มายังปัญหา NP-Complete (หรือ NP Hard ต่อ) นั้นเป็นขั้นตอนที่ยากและซับซ้อน เนื่องจากต้องแสดงให้เห็นว่าสามารถแปลงปัญหาหนึ่งไปเป็นอีกปัญหาหนึ่งได้ในเวลาพหุนามด้วย

เมื่อกลับมาดูตามนิยาม

• NP-Complete เป็นกลุ่มของปัญหายากที่สุดในชั้น NP และปัญหาอื่นๆ ทุกปัญหาในชั้น NP สามารถถูกลดรูป (reduce) มาเป็นปัญหา NP Complete ได้ในเวลาพหุนาม
• NP-Hard คือปัญหาที่ยากไม่น้อยกว่าหรือยากกว่าปัญหา NP-Complete โดย ต้องแสดงให้เห็นว่าปัญหา NP-Complete สามารถถูกลดรูปมาเป็นปัญหานั้นได้ในเวลาพหุนาม

ดังนั้น จากนิยามนี้ พอจะบอกได้ว่า NP Complete นั้นยากกว่า NP และ NP Hard นั้น ยากกว่า NP-Complete แต่ก็ไม่ได้หมายความว่า NP-Hard เป็นปัญหายากที่สุดในชั้น NP เนื่องจาง NP-Hard นั้นอาจจะไม่ได้อยู่ในชั้น NP เลยก็ได้ จึงไม่สามารถเปรียบเทียบความยากได้โดยตรงกับปัญหาในชั้น NP ได้

คำถามเลยเพิ่มเติมมาว่า “แล้วปัญหาอะไรคือ ปัญหาของ NP Hard ที่ไม่ใช่ NP Complete” สิ่งที่เราจะต้องทำมีอยู่ 2 อย่างคือ

1. แสดงให้เห็นว่าปัญหานั้นไม่ได้อยู่ในชั้น NP (Non-deterministic Polynomial time)

• ชั้น NP คือชั้นของปัญหาที่เราสามารถตรวจสอบคำตอบได้ในเวลาพหุนาม
• หากไม่สามารถแสดงได้ว่ามีวิธีตรวจสอบคำตอบในเวลาพหุนาม แสดงว่าปัญหานั้นไม่ได้อยู่ในชั้น NP

2. แสดงให้เห็นว่าปัญหา NP-Complete สามารถถูกลดรูปมาเป็นปัญหานั้นได้ในเวลาพหุนาม (แบบเดียวกันกับที่ทำระหว่าง NP สู่ NP Complete)

หากปัญหาใดสามารถแสดงได้ว่าเป็นไปตามเงื่อนไขทั้งสองข้อข้างต้น คือไม่ได้อยู่ในชั้น NP แต่ปัญหา NP-Complete สามารถถูกลดรูปมาเป็นปัญหานั้นได้ในเวลาพหุนาม แสดงว่าปัญหานั้นเป็น NP-Hard แต่ไม่ใช่ NP-Complete นั่นเอง (และเป็นที่มาของภาพด้านบน)

** เราจะไม่ลง detail การพิสูจน์กันตอนนี้ เราจะให้ทุกคนเห็นภาพก่อนว่า ปัญหาที่เรากำลังจะแก้กันต่อจากนี้ หลายๆอันก็ลดรูปจาก NP ลงมาเพื่อให้สามารถแก้ปัญหาในเวลา P ออกมาได้ แต่เมื่อ input ขนาดใหญ่มาก ท้ายที่สุด ก็จะยังต้องกลับมาสู่รากฐานของปัญหา NP Problem อยู่ดี ใครที่สนใจเรื่องนี้เชิงลึกอ่านเพิ่มเติมได้ที่ https://en.wikipedia.org/wiki/Karp's_21_NP-complete_problems

NP Problem กับ Backtracking

จากเนื้อหาด้านบน จะเห็นว่าปัญหา NP คือปัญหาที่เราสามารถตรวจสอบคำตอบได้ในเวลาพหุนาม แต่ยังไม่พบวิธีการหาคำตอบในเวลาพหุนาม หมายความว่า แม้เราจะสามารถตรวจสอบความถูกต้องของคำตอบได้อย่างรวดเร็ว แต่การหาคำตอบที่ถูกต้องนั้นกลับเป็นเรื่องที่ยาก

ซึ่ง Backtracking เป็นเทคนิคการออกแบบ algorithm ที่มักนำมาใช้ในการแก้ปัญหา NP เนื่องจากปัญหาเหล่านี้มักเกี่ยวข้องกับการค้นหาคำตอบจากทางเลือกจำนวนมาก ที่ถึงแม้ว่า Backtracking จะไม่ใช่วิธีการที่ประสิทธิภาพที่สุด แต่ก็เป็นเทคนิคที่สำคัญในการแก้ปัญหา NP เนื่องจากสามารถค้นหาคำตอบที่ถูกต้องได้ แม้จะต้องใช้เวลาในการประมวลผลมากก็ตาม

วิธีการ Backtracking จะทำงานโดยการสร้างผลเฉลยแบบค่อยเป็นค่อยไป โดยจะเพิ่มส่วนประกอบของผลเฉลยทีละส่วน และตรวจสอบว่าผลเฉลยนั้นเป็นไปตามเงื่อนไขที่กำหนดหรือไม่ หากไม่เป็นไปตามเงื่อนไข ก็จะย้อนกลับไปแก้ไขส่วนประกอบก่อนหน้า

ตัวอย่างการใช้ Backtracking ในการแก้ปัญหา NP เช่น การแก้ปัญหา N-Queens Problem ที่เราพึ่งทำไป ซึ่งเป็นปัญหาการค้นหาวิธีวาง Queen บนกระดานขนาด N*N โดยไม่ให้ Queen ตัวใดคุกคามกันได้

แต่ ในบางกรณี เทคนิค Backtracking อาจไม่สามารถแก้ปัญหา NP ได้เมื่อขนาดของข้อมูลนำเข้ามีขนาดใหญ่ เนื่องจาก

1. ปริมาณการคำนวณที่มากเกินไป Backtracking จำเป็นต้องสร้างผลเฉลยแบบค่อยเป็นค่อยไป โดยเพิ่มส่วนประกอบทีละส่วน เมื่อขนาดของข้อมูลนำเข้าใหญ่ขึ้น จำนวนทางเลือกในการสร้างผลเฉลยก็จะเพิ่มขึ้นเป็นเลขยกกำลัง ทำให้ปริมาณการคำนวณมีจำนวนมหาศาล (ตามหลักการของ NP)
2. ความซับซ้อนเชิงเวลาสูงมาก ความซับซ้อนเชิงเวลาของ Backtracking มักอยู่ในระดับ O(n!) หรือ O(2^n) ซึ่งเป็น function เลขชี้กำลังที่เติบโตอย่างรวดเร็วมาก เมื่อขนาดของข้อมูลนำเข้าใหญ่ขึ้น เวลาในการประมวลผลก็จะเพิ่มขึ้นอย่างรวดเร็วจนไม่สามารถยอมรับได้ (อย่างน้อยที่สุดก็ใน problem solving)
3. ข้อจำกัดด้านหน่วยความจำ Backtracking ต้องเก็บข้อมูลผลเฉลยแบบค่อยเป็นค่อยไปในหน่วยความจำ เมื่อขนาดของข้อมูลนำเข้าใหญ่ขึ้น ปริมาณหน่วยความจำที่ต้องใช้ก็จะเพิ่มขึ้นมาก จนอาจเกินขีดจำกัดของหน่วยความจำที่มีอยู่
4. ความซับซ้อนของปัญหา บางปัญหา NP มีความซับซ้อนสูงมาก มีเงื่อนไขและข้อจำกัดมากมาย ทำให้การ Backtracking ไม่สามารถหาคำตอบที่ดีที่สุดได้ในเวลาที่สมเหตุสมผล

ซึ่ง โดยปกติแล้วจะพิจารณาใช้ Backtracking หรือไม่ ควรตรวจสอบจาก

1. ขนาดของปัญหา Backtracking เหมาะสำหรับปัญหาขนาดเล็กถึงปานกลาง เนื่องจากมี Time Complexity ที่สูง หากปัญหามีขนาดใหญ่มาก Backtracking อาจไม่สามารถหาคำตอบได้ในเวลาที่สมเหตุสมผลได้
2. เงื่อนไขและข้อจำกัดปัญหาที่มีเงื่อนไขและข้อจำกัดไม่มากนัก จะเหมาะสมกับการใช้ Backtracking มากกว่าปัญหาที่มีเงื่อนไขและข้อจำกัดซับซ้อน เนื่องจากการตรวจสอบเงื่อนไขจะทำได้ง่ายขึ้น
3. โครงสร้างของปัญหา ปัญหาที่มีโครงสร้างเป็นลำดับชั้น (Tree-like structure) หรือสามารถจัดเรียงทางเลือกเป็นลำดับชั้นได้ จะเหมาะสมกับการใช้ Backtracking มากกว่า เนื่องจากสามารถสร้างผลเฉลยแบบค่อยเป็นค่อยไปได้ง่ายกว่า

ตัวอย่างปัญหา NP ที่เหมาะสมกับการใช้การย้อนรอยถอยหลัง ได้แก่

• ปัญหาการวางตัว Queen บนกระดาน (N-Queens Problem)
• ปัญหาการแบ่งกลุ่ม (Partition Problem)
• ปัญหาการจัดตารางงาน (Job Scheduling Problem)

นี่คือสาระสำคัญของ NP และ Backtracking ดังนั้น จริงๆแล้ว Backtracking ถูก design มาเพื่อแก้ปัญหากับพวก NP กับเคสที่ต้องมีการลองให้ครบทุกเคส เหมือนๆกับเคสของ N Queens แต่ทั้งนี้เนื่องจาก โจทย์เหล่านี้อยู่ในตระกูลของ NP การเติบโตของเวลาก็จะไวขึ้นเช่นกัน ดังนั้น Backtracking จึงถูก design มาใช้กับปัญหาที่มีขนาด “ไม่ใหญ่มาก” ตัวอย่างในหน้าต่อไปจะให้เห็นเพิ่มเติมว่าโจทย์อื่นๆของ Backtracking ที่สามารถ Solve ได้จะมีประมาณไหนบ้าง