Shortest part
Shortest Path คืออะไร ?
คือปัญหาในทฤษฎีกราฟที่เกี่ยวข้องกับการหาเส้นทางระหว่างจุดยอด (vertex) สองจุดในกราฟ โดยที่ผลรวมของน้ำหนัก (weight) ของเส้นเชื่อมต่อ (edge) ในเส้นทางนั้นมีค่าน้อยที่สุด
กราฟสามารถเป็นได้ทั้งแบบมีทิศทาง (directed) หรือไม่มีทิศทาง (undirected) และอาจมีน้ำหนักของเส้นเชื่อมต่อเป็นค่าบวกหรือลบก็ได้ เส้นทางที่สั้นที่สุดจะประกอบด้วยจุดยอดไม่เกิน n-1 เส้นเชื่อมต่อ เนื่องจากเส้นทางที่สั้นที่สุดไม่ควรมีวงจร (cycle) เพราะไม่จำเป็นต้องผ่านจุดยอดใดซ้ำอีก
อัลกอริทึมที่ใช้ในการแก้ปัญหาเส้นทางที่สั้นที่สุด ได้แก่
- Dijkstra's Algorithm - ใช้หาเส้นทางที่สั้นที่สุดจากจุดยอดต้นทางไปยังจุดยอดอื่นๆ ��ทั้งหมดในกราฟแบบมีน้ำหนักที่ไม่ติดลบ มีความซับซ้อนเวลา O(V + E log V)
- Bellman-Ford Algorithm - ใช้หาเส้นทางที่สั้นที่สุดจากจุดยอดต้นทางไปยังจุดยอดอื่นๆ ในกราฟแบบมีน้ำหนักที่อาจติดลบได้ มีความซับซ้อนเวลา O(VE)
- Floyd-Warshall Algorithm - ใช้หาเส้นทางที่สั้นที่สุดระหว่างจุดยอดทุกคู่ในกราฟ มีความซับซ้อนเวลา O(V^3)
สำหรับกราฟแบบไม่มีน้ำหนัก เราสามารถใช้ Breadth-First Search (BFS) เพื่อหาเส้นทางที่สั้นที่สุดได้ โดยมีความซับซ้อนเวลาเพียง O(V+E) เท่านั้น
โดย ตัวอย่างปัญหาเส้นทางที่สั้นที่สุดในทฤษฎีกราฟ มีดังนี้
- การหาเส้นทางที่ใช้เวลาน้อยที่สุดระหว่างสองสถานที่บนแผนที่ เช่น การหาเส้นทางที่ใช้เวลาน้อยที่สุดจากบ้านไปที่ทำงาน โดยแผนที่ถูกแทนด้วยกราฟที่มีจุดยอดแทนสถานที่ต่างๆ และเส้นเชื่อมต่อแทนถนน โดยน้ำหนักของเส้นเชื่อมต่อคือระยะทางหรือเวลาที่ใช้ในการเดิน��ทาง
- การหาเส้นทางที่ประหยัดที่สุดในการขนส่งสินค้าจากโรงงานไปยังร้านค้าต่างๆ โดยเส้นทางการขนส่งถูกแทนด้วยกราฟ จุดยอดคือโรงงานและร้านค้า ส่วนเส้นเชื่อมต่อคือเส้นทางขนส่ง น้ำหนักของเส้นเชื่อมต่อคือค่าใช้จ่ายในการขนส่งผ่านเส้นทางนั้น
- การหาเส้นทางที่เชื่อมต่อคอมพิวเตอร์ในเครือข่ายที่มีประสิทธิภาพสูงสุด เช่น การส่งข้อมูลจากคอมพิวเตอร์หนึ่งไปยังอีกเครื่องหนึ่งผ่านเครือข่าย โดยเครือข่ายถูกแทนด้วยกราฟ จุดยอดคือคอมพิวเตอร์ เส้นเชื่อมต่อคือการเชื่อมต่อระหว่างคอมพิวเตอร์ น้ำหนักของเส้นเชื่อมต่อคือความเร็วหรือแบนด์วิดท์ของการเชื่อมต่อ
- การหาเส้นทางที่สั้นที่สุดในเกมคอมพิวเตอร์ เช่น การหาเส้นทางที่สั้นที่สุดจากจุดเริ่มต้นไปยังจุดหมายปลายทางในเกมวางแผนกลยุทธ์ โดยแผนที่ในเกมถูกแทนด้วยกราฟ จุดยอดคือสถานที่ต่างๆ เส้นเชื่อมต่อคือเส้นทางที่เชื่อมระหว่างสถานที่ น้ำหนักของเส้นเชื่อมต่อคือระยะทางหรือเวลาที่ใช้ในการเดินทาง
- การหาเส้นทางที่สั้นที่สุดในโครงข่ายการขนส่งสาธารณะ เช่น การหาเส้นทางที่ใช้เวลาน้อยที่สุดในการเดินทางจากสถานีรถไฟหนึ่งไปยังอีกสถานีหนึ่ง โดยโครงข่ายรถไฟถูกแทนด้วยกราฟ จุดยอดคือสถานีรถไฟ เส้นเชื่อมต่อคือเส้นทางรถไฟ น้ำหนักของเส้นเชื่อมต่อคือเวลาที่ใช้ในการเดินทางระหว่างสถานี
Dijkstra's Algorithm
Dijkstra's Algorithm คืออัลกอริทึมที่ใช้ในการหาเส้นทางที่สั้นที่สุดจากจุดเริ่มต้นไปยังจุดอื่นๆ ทั้งหมดในกราฟแบบมีน้ำหนัก (weighted graph) โดยมีขั้นตอนดังนี้
ไอเดียของมันเริ่มต้นมาจาก Greedy Algorithm
- กำหนดให้ทุกจุดยอดมีระยะทา�งเป็นอนันต์ (infinity) ยกเว้นจุดเริ่มต้นที่มีระยะทางเป็น 0
- สร้าง priority queue เพื่อเก็บจุดยอดที่ยังไม่ได้เยี่ยมชม โดยเรียงลำดับตามระยะทางจากจุดเริ่มต้น
- ตราบใดที่ priority queue ไม่ว่าง ให้ทำดังนี้:
- นำจุดยอดที่มีระยะทางน้อยที่สุดออกจาก priority queue (เรียกว่าจุด u)
- สำหรับจุดยอดข้างเคียงทุกจุดของ u (เรียกว่าจุด v):
- คำนวณระยะทางใหม่จากจุดเริ่มต้นไปยัง v ผ่าน u
- ถ้าระยะทางใหม่สั้นกว่าระยะทางเดิมที่เคยบันทึกไว้ ให้อัปเดตระยะทางใหม่ และอัปเดตใน priority queue ด้วย
- สิ้นสุดอัลกอริทึม เมื่อได้ระยะทางที่สั้นที่สุดจากจุดเริ่มต้นไปยังทุกจุดแล้ว
ตัวอย่างการเขียนโค้ด C++ สำหรับ Dijkstra's Algorithm
#include <iostream>
#include <limits>
#include <queue>
#include <vector>
using namespace std;
vector<int> dijkstra(vector<vector<int>> &graph, int src) {
int n = graph.size();
vector<int> dist(n, numeric_limits<int>::max());
dist[src] = 0;
priority_queue<pair<int, int>, vector<pair<int, int>>,
greater<pair<int, int>>>
pq;
pq.push({0, src});
while (!pq.empty()) {
int u = pq.top().second;
pq.pop();
for (int v = 0; v < n; v++) {
if (graph[u][v] != 0) {
int new_dist = dist[u] + graph[u][v];
if (new_dist < dist[v]) {
dist[v] = new_dist;
pq.push({new_dist, v});
}
}
}
}
return dist;
}
int main() {
vector<vector<int>> graph = {
{0, 4, 0, 0, 0, 0, 0, 8, 0},
{4, 0, 8, 0, 0, 0, 0, 11, 0},
{0, 8, 0, 7, 0, 4, 0, 0, 2},
{0, 0, 7, 0, 9, 14, 0, 0, 0},
{0, 0, 0, 9, 0, 10, 0, 0, 0},
{0, 0, 4, 14, 10, 0, 2, 0, 0},
{0, 0, 0, 0, 0, 2, 0, 1, 6},
{8, 11, 0, 0, 0, 0, 1, 0, 7},
{0, 0, 2, 0, 0, 0, 6, 7, 0}
};
int src = 0;
vector<int> shortest_dists = dijkstra(graph, src);
cout << "Shortest distances from node " << src << ":" << endl;
for (int i = 0; i < shortest_dists.size(); i++) {
cout << "To node " << i << ": " << shortest_dists[i] << endl;
}
return 0;
}
และนี่คือภาพกราฟสำหรับข้อนี้
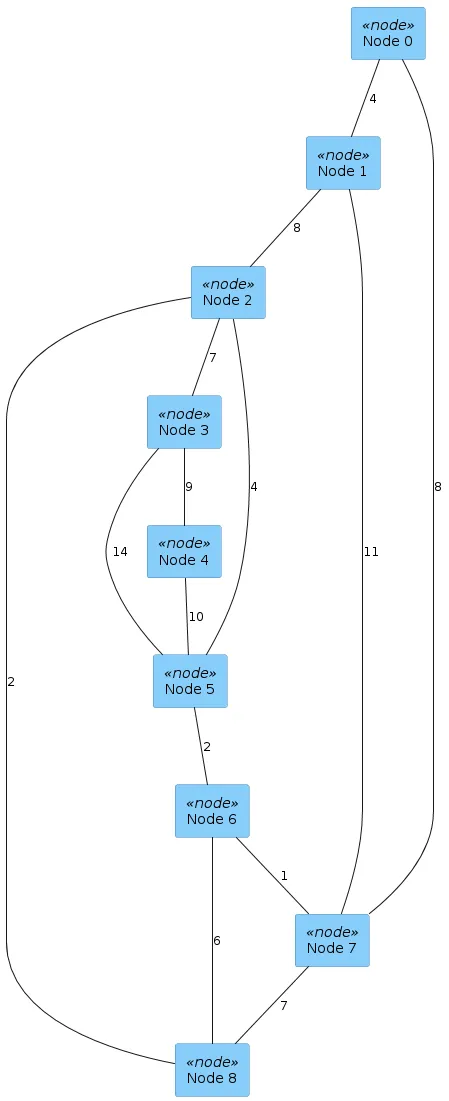
ในกราฟนี้ มีจุดยอดทั้งหมด 9 จุด (0 ถึง 8) และมีเส้นเชื่อมต่อพร้อมน้ำหนักระหว่างจุดยอดต่างๆ ตามที่กำหนดในโค้ด เมื่อรันโค้ด ผลลัพธ์จะแสดงระยะทางที่สั้นที่สุดจากจุดเริ่มต้น (ในที่นี้คือจุด 0) ไปยังทุกจุดในกราฟ โดยใช้ Dijkstra's Algorithm
Bellman-Ford Algorithm
Bellman-Ford คือวิธีการหาค่าระยะทางที่สั้นที่ส�ุดจากจุดเริ่มต้นไปยังจุดต่างๆ ในกราฟที่มีการถ่วงน้ำหนัก ซึ่งอาจมีน้ำหนักเป็นค่าลบได้
หลักการทำงานของ Bellman-Ford คือทำการอัพเดทราคาตั๋วทุกขอบในกราฟทั้งหมด และทำซ้ำตามจำนวนจุดในกราฟลบหนึ่งครั้ง วิธีนี้ทำให้สามารถตรวจจับรอบลบได้ เพราะถ้ามีการอัพเดทราคาตั๋วหลังจากทำซ้ำครบแล้ว หมายถึงมีรอบลบอยู่ในกราฟ
ขั้นตอนการทำงานหลักๆ มีดังนี้:
- กำหนดระยะทางจากจุดเริ่มต้นไปยังจุดอื่นๆ ทั้งหมดเป็นอนันต์ (infinity) ยกเว้นจุดเริ่มต้นที่กำหนดเป็นศูนย์
- ทำการอัพเดทราคาตั๋วตามขอบของกราฟทั้งหมด
- ทำซ้ำขั้นตอนที่สองตามจำนวนจุดในกราฟลบหนึ่งครั้ง
- ตรวจสอบว่ามีการอัพเดทราคาตั๋วอีกหรือไม่หลังจากทำซ้ำครบแล้ว หากมีหมายถึงมีรอบลบในกราฟ
อัลกอริธึมนี้มีประโยชน์ในกรณีที่กราฟมีการถ่วงน้ำหนักที่เป็นค่าลบ ซึ่งไม่สามาร�ถใช้วิธี Dijkstra ได้
และนี่คือ code c++ ของ Bellman-Ford
#include <climits>
#include <iostream>
#include <vector>
using namespace std;
// โครงสร้างที่ใช้แทนขอบ (edge) ของกราฟ
struct Edge {
int src, dest, weight;
};
// ฟังก์ชัน Bellman-Ford
void bellmanFord(int V, int E, vector<Edge> &edges, int src) {
// สร้างระยะทางจากจุดเริ่มต้นไปยังจุดอื่นๆ และกำหนดค่าเริ่มต้นเป็นอนันต์ (infinity)
vector<int> distance(V, INT_MAX);
distance[src] = 0;
// ทำซ้ำตามจำนวนจุดในกราฟลบหนึ่งครั้ง
for (int i = 1; i <= V - 1; ++i) {
for (int j = 0; j < E; ++j) {
int u = edges[j].src;
int v = edges[j].dest;
int weight = edges[j].weight;
// ถ้าระยะทางจา�กจุด u ไป v ผ่านขอบนี้น้อยกว่าเดิม ให้ปรับระยะทางใหม่
if (distance[u] != INT_MAX && distance[u] + weight < distance[v]) {
distance[v] = distance[u] + weight;
}
}
}
// ตรวจสอบรอบลบ
for (int i = 0; i < E; ++i) {
int u = edges[i].src;
int v = edges[i].dest;
int weight = edges[i].weight;
if (distance[u] != INT_MAX && distance[u] + weight < distance[v]) {
cout << "กราฟมีรอบลบ\n";
return;
}
}
// แสดงระยะทางที่คำนวณได้
cout << "ระยะทางจากจุดเริ่มต้นถึงจุดอื่นๆ:\n";
for (int i = 0; i < V; ++i) {
cout << "จุด " << i << " : " << distance[i] << "\n";
}
}
int main() {
int V = 5; // จำนวนจุดในกราฟ
int E = 8; // จำนวนขอบในกราฟ
vector<Edge> edges(E);
// กำหนดค่าขอบของกราฟ
edges[0] = {0, 1, -1};
edges[1] = {0, 2, 4};
edges[2] = {1, 2, 3};
edges[3] = {1, 3, 2};
edges[4] = {1, 4, 2};
edges[5] = {3, 2, 5};
edges[6] = {3, 1, 1};
edges[7] = {4, 3, -3};
int src = 0; // จุดเริ่มต้น
bellmanFord(V, E, edges, src);
return 0;
}
และนี่คือภาพกราฟ
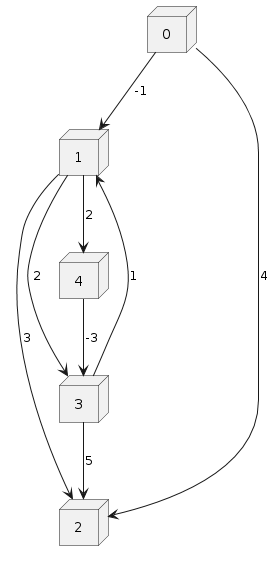
คำอธ�ิบาย code
- โครงสร้าง Edge: ใช้แทนขอบของกราฟที่ประกอบด้วยจุดเริ่มต้น (src), จุดปลายทาง (dest), และน้ำหนัก (weight) ของขอบนั้น
- ฟังก์ชัน bellmanFord: ทำหน้าที่คำนวณระยะทางที่สั้นที่สุดจากจุดเริ่มต้นไปยังจุดอื่นๆ ในกราฟ
- สร้างเวกเตอร์ระยะทางที่กำหนดค่าเริ่มต้นเป็นอนันต์ และตั้งค่าจุดเริ่มต้นเป็นศูนย์
- ทำซ้ำการอัพเดทราคาตั๋วตามจำนวนจุดในกราฟลบหนึ่งครั้ง
- ตรวจสอบว่ามีรอบลบหรือไม่
- แสดงระยะทางที่คำนวณได้
- ฟังก์ชัน main: กำหนดจำนวนจุดและขอบของกราฟ พร้อมทั้งค่าของขอบแต่ละขอบ และเรียกใช้ฟังก์ชัน bellmanFord
Floyd-Warshall Algorithm
Floyd-Warshall Algorithm เป็นหนึ่งในอัลกอริทึมที่ใช้สำหรับหาค่าเส้นทางที่สั้นที่สุดระหว่างทุกคู่ของจุดในกราฟที่มีน้ำหนักบนเส้นเชื่อม (weighted graph) ซึ่งอัลกอริทึมนี้สามารถใช้ได้กับกราฟที่มีน้ำหนักเป็นลบได้ด้วย
หลักการของ Floyd-Warshall Algorithm
- เริ่มต้น: สร้างตารางระยะทาง (distance matrix)
dist[][]โดยกำหนดค่าเริ่มต้นให้เป็นน้ำหนักของเส้นเชื่อมระหว่างจุด หากไม่มีเส้นเชื่อมระหว่างจุดนั้น ๆ กำหนดเป็นอนันต์ (infinity) ยกเว้นระยะทางจากจุดไปหาจุดตัวเองกำหนดเป็นศูนย์ (0) - กระบวนการปรับปรุงระยะทาง:
- ใช้จุดทั้งหมดในกราฟเป็น "จุดผ่านทาง" (intermediate vertex) ทีละจุด
- สำหรับแต่ละจุดผ่านทาง
k:- ตรวจสอบคู่ของจุด
iและjทุกคู่ - ปรับปรุงค่า
dist[i][j]โดยพิจารณาว่าการผ่านทางจุดkจะทำให้ระยะทางสั้นลงหรือไม่ - สูตรในการปรับปรุงค่า:
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])
- ตรวจสอบคู่ของจุด
- สิ้นสุด: เมื่อทำกระบวนการครบทุกจุดผ่านทางแล้ว ตาราง
dist[][]จะเก็บค่าระยะทางที่สั้นที่สุดระหว่างทุกคู่ของจุดในกราฟ
#include <iomanip>
#include <iostream>
#include <vector>
using namespace std;
#define INF 99999
void printSolution(const vector<vector<int>> &dist, int V) {
cout << "The following matrix shows the shortest distances between every "
"pair of vertices\n";
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
if (dist[i][j] == INF)
cout << setw(5) << "INF";
else
cout << setw(5) << dist[i][j];
}
cout << endl;
}
}
void floydWarshall(vector<vector<int>> &graph, int V) {
vector<vector<int>> dist = graph;
for (int k = 0; k < V; k++) {
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
if (dist[i][k] != INF && dist[k][j] != INF &&
dist[i][k] + dist[k][j] < dist[i][j]) {
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
}
printSolution(dist, V);
}
int main() {
int V = 4;
vector<vector<int>> graph = {
{0, 5, INF, 10}, {INF, 0, 3, INF}, {INF, INF, 0, 1}, {INF, INF, INF, 0}};
floydWarshall(graph, V);
return 0;
}
รูปร่างของกราฟ
ความซับซ้อนของโค้ด (Code Complexity) Floyd-Warshall Algorithm นี้เป็น 𝑂(𝑉3)O(V3) โดยที่ 𝑉V คือจำนวนจุด (vertices) ในกราฟ เนื่องจากโค้ดมีการใช้การวนลูปสามชั้น (nested loop) ในการปรับปรุงระยะทางระหว่างทุกคู่ของจุด
การวิเคราะห์ความซับซ้อน
- การสร้างตารางระยะทางเริ่มต้น:
- การสร้างตารางระยะทางจากกราฟเริ่มต้นมีความซับซ้อนเป็น 𝑂(𝑉2)O(V2) แต่ถือว่าเล็กเมื่อเทียบกับการวนลูปสามชั้น ดังนั้นไม่ถือเป็นส่วนสำคัญในการคำนวณความซับซ้อนโดยรวม
- การวนลูปสามชั้น:
- ลูปแรก (ค่า 𝑘k ที่ใช้เป็นจุดผ่านทาง) ทำงาน 𝑉V ครั้ง
- ลูปที่สอง (ค่า 𝑖i ที่ใช้เป็นจุดเริ่มต้น) ทำงาน 𝑉V ครั้งสำหรับแต่ละค่าขอ�ง 𝑘k
- ลูปที่สาม (ค่า 𝑗j ที่ใช้เป็นจุดปลายทาง) ทำงาน 𝑉V ครั้งสำหรับแต่ละค่าของ 𝑖i และ 𝑘k
ดังนั้น การวนลูปสามชั้นนี้มีจำนวนครั้งของการทำงานทั้งหมดเป็น 𝑉×𝑉×𝑉=𝑉3V×V×V=V3
สรุป
- Time Complexity: 𝑂(𝑉3)O(V3)
- Space Complexity: 𝑂(𝑉2)O(V2) เนื่องจากต้องใช้พื้นที่ในการเก็บตารางระยะทาง (distance matrix) ที่มีขนาด 𝑉×𝑉V×V