โจทย์พื้นฐาน

ตัวอย่าง Greedy Problem เทียบกับ Bluteforce

เรามาเริ่มจากโจทย์ที่ง่ายที่สุดก่อน
ปัญหา: จงหาจำนวนเหรียญน้อยที่สุดที่ต้องใช้เพื่อจ่ายเงินจำนวน X บาท โดยมีเหรียญให้เลือกใช้ดังนี้ 1, 2, 5, 10 บาท
หากเราเลือกวิธีแก้ปัญหาแบบปกติ (Brute Force) สิ่งที่เราจะทำคือ

ลองทุกวิธีที่เป็นไปได้ในการจ่ายเงิน X บาท ด้วยเหรียญที่มี และค่อยเลือกวิธีที่ใช้เหรียญน้อยที่สุด

ตัวอย่าง code แก้ปัญหาแบบ brute force (Recursive Brute force)

#include <iostream>
#include <vector>
using namespace std;

int coinChange(vector<int> &coins, int amount) {
  if (amount == 0)
    return 0;
  int result = INT_MAX;
  for (int coin : coins) {
    if (coin <= amount) {
      int subResult = coinChange(coins, amount - coin);
      if (subResult != INT_MAX)
        result = min(result, 1 + subResult);
    }
  }
  return result == INT_MAX ? -1 : result;
}

int main() {
  vector<int> coins = {1, 2, 5, 10};
  int amount = 27;
  cout << coinChange(coins, amount) << endl;
  return 0;
}

โดย Time Complexity ของ coinChange คือ O(n^amount) โดยที่ n คือจำนวนเหรียญ และ amount คือจำนวนเงินที่ต้องการ ใน worst case ที่สุด

แสดงวิธีทำ คำนวณ time complexity โดย time complexity สามารถเขียนได้ในรูปแบบนี้ ในทุกๆครั้งที่มีการ recursive จะใช้เวลาตามสมการนี้
T(amount) = n * T(amount - coin) + O(1)
- โดยจำนวนการทำจะลดลงไปตาม amount - coin ที่ใช้

โดยใน worst case ที่สุด recursion จะดำดิ่งลงไปมากที่สุดเท่ากับ amount (มองเหมือนแลกทีละเหรียญจนหมด) ดังนั้น time complexity สามารถเขียนได้ในรูปแบบเป็น

T(amount) = n * (n * (n * (... (n * O(1))...)))

โดยจำนวน recursive call เท่ากับ amount ดังนั้น time complexity สามารถเขียนในรูปแบบที่ง่ายที่สุดเป็น

T(amount) = O(n^amount)

โดยหากเราลองเปลี่ยนวิธีแก้ปัญหาเป็นแบบ Greedy ดู ด้วยการ

เลือกเหรียญ "ที่มีค่ามากที่สุด" ที่ไม่เกิน X มาใช้ก่อน หากเหรียญมีค่ามากกว่า X บาทแล้ว จะไปยังเหรียญต่อไปที่มีมูลค่าน้อยกว่าและทำซ้ำเช่นเดิม
ทำซ้ำจนกว่าจะได้จำนวนเงินครบ X บาท

ตัวอย่างโค้ด C++ แบบ Greedy:

#include <iostream>
#include <vector>
using namespace std;

int coinChange(vector<int> &coins, int amount) {
  int count = 0;
  for (int i = coins.size() - 1; i >= 0; i--) {
    while (amount >= coins[i]) {
      amount -= coins[i];
      count++;
    }
  }
  return amount == 0 ? count : -1;
}

int main() {
  vector<int> coins = {1, 2, 5, 10};
  int amount = 27;
  cout << coinChange(coins, amount) << endl;
  return 0;
}

จากตัวอย่าง จะเห็นว่าวิธี Greedy ให้ผลลัพธ์ที่ถูกต้องและรวดเร็วกว่าวิธี Brute Force มาก เพราะไม่ต้องลองทุกความเป็นไปได้ แต่เลือกเหรียญที่ใหญ่ที่สุดมาใช้ก่อนเลย
อย่างไรก็ตาม Greedy Algorithm ไม่ได้ให้คำตอบที่ดีที่สุดเสมอไป ในบางปัญหาอาจให้ผลลัพธ์ที่ผิดได้ ดังนั้นจึงต้องวิเคราะห์ปัญหาให้ดีก่อนเลือกใช้ Greedy

Fractional Knapsack

ปัญหา Fractional Knapsack คือปัญหาการเลือกของใส่ในกระเป๋าที่มีขนาดจำกัดให้ได้มูลค่ามากที่สุด โดยของแต่ละชิ้นมีน้ำหนักและมูลค่าต่างกัน และสามารถแบ่งของแต่ละชิ้นเป็นส่วนๆได้
ขั้นตอนวิธีแบบ Greedy ในการแก้ปัญหา Fractional Knapsack มีดังนี้

หาอัตราส่วนมูลค่าต่อน้ำหนัก (value/weight) ของของแต่ละชิ้น
เรียงลำดับของจากอัตราส่วนมูลค่าต่อน้ำหนักมากไปน้อย
เลือกของที่มีอัตราส่วนมากที่สุดใส่ในกระเป๋าก่อน ถ้าใส่ทั้งชิ้นได้ก็ใส่ทั้งชิ้น ถ้าใส่ไม่หมดก็ใส่เท่าที่พอดีกับน้ำหนักที่เหลือ (เลือกใส่เท่าที่ใส่ได้)
ทำซ้ำขั้นตอนที่ 3 กับของชิ้นถัดไปที่มีอัตราส่วนมากที่สุด จนกว่ากระเป๋าจะเต็มหรือของจะหมด

ตัวอย่างโค้ด C++ ที่ใช้ Greedy Algorithm แก้ปัญหา Fractional Knapsack

#include <bits/stdc++.h>
using namespace std;

struct Item {
  int value, weight;
  Item(int value, int weight) : value(value), weight(weight) {}
};

bool cmp(struct Item a, struct Item b) {
  double r1 = (double)a.value / a.weight;
  double r2 = (double)b.value / b.weight;
  return r1 > r2;
}

double fractionalKnapsack(int W, struct Item arr[], int n) {
  sort(arr, arr + n, cmp);

  int curWeight = 0;
  double finalvalue = 0.0;

  for (int i = 0; i < n; i++) {
    if (curWeight + arr[i].weight <= W) {
      curWeight += arr[i].weight;
      finalvalue += arr[i].value;
    } else {
      int remain = W - curWeight;
      finalvalue += arr[i].value * ((double)remain / arr[i].weight);
      break;
    }
  }

  return finalvalue;
}

int main() {
  int W = 50;
  Item arr[] = {{60, 10}, {100, 20}, {120, 30}};
  int n = sizeof(arr) / sizeof(arr[0]);

  cout << "Maximum value we can obtain = " << fractionalKnapsack(W, arr, n);
  return 0;
}

ความซับซ้อนของอัลกอริทึมนี้คือ O(n log n) เนื่องจากมีการเรียงลำดับข้อมูล ซึ่งเร็วกว่าการแก้แบบ Brute Force ที่ต้องลองทุกความเป็นไปได้แน่นอน และมั่นใจได้ว่าถูกต้อง เพราะเราเรียงตาม "มูลค่าโดยรวมสูงสุด" (value/weight) ซึ่งเป็นเคสที่ดีที่สุด เท่าที่จะเลือกได้แล้ว
Note: ปัญหานี้แตกต่างกับ 0/1 Knapsack ที่เราจะพูดใน Dynamic Programming นะครับ โดยปัญหา 0/1 Knapsack นั้นจะคล้ายๆกัน แต่แตกต่างกันตรงที่ "ไม่สามารถแบ่งสิ่งของได้ ต้องเลือกเอาทั้งชิ้นหรือไม่เอาเลยเท่านั้น" จึงทำให้ไม่สามารถใช้วิธีการเดียวกันในการแก้ปัญหาได้

Activity Selection Problem

เป็นปัญหาคลาสสิกในวิทยาการคอมพิวเตอร์ที่สามารถแก้ได้ด้วยอัลกอริทึมแบบ Greedy ในปัญหานี้ เราจะได้รับชุดของกิจกรรมที่ต้องทำในช่วงเวลาที่กำหนด โดยแต่ละกิจกรรมจะมีเวลาเริ่มต้นและเวลาสิ้นสุด เป้าหมายคือการเลือกจำนวนกิจกรรมสูงสุดที่สามารถทำได้โดยไม่มีกิจกรรมใดทับซ้อนกัน
สมมุติว่า เรากำหนดกิจกรรมแต่ละแบบให้เป็นแบบนี้ โดย

ให้ S = {a[1], …, a[n]} เป็น set ของ n กิจกรรม
แต่ละกิจกรรม a[i] ต้องการเวลาในการทำงาน โดยในช่วงเวลาเริ่มต้นที่ s[i] และสิ้นสุดก่อน f[i] ใช้เวลาตั้งแต่ [si, fi)

เช่นตามตัวอย่างนี้

เมื่อแสดงเป็นภาพก็จะมีหน้าตาเป็นประมาณนี้

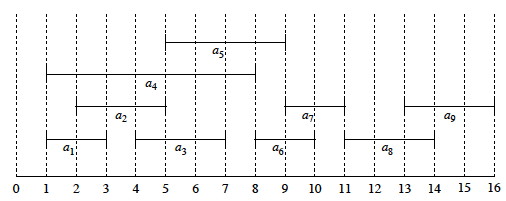
โดยจากตัวอย่างนี้ จะแปลว่า

กิจกรรม a[1] เริ่มต้นที่เวลา 1 และสิ้นสุดที่เวลา 3
กิจกรรม a[2] เริ่มต้นที่เวลา 2 และสิ้นสุดที่เวลา 4

เป็นต้น
โดย โจทย์ของ Activity Selection Problem คือการเลือก กิจกรรม "ที่เวลาไม่ซ้อนทับกัน" โดยมีเป้าหมายคือ การเลือกจำนวนกิจกรรมสูงสุดที่สามารถทำได้โดยไม่มีกิจกรรมใดทับซ้อนกัน โดย

รูปแบบที่สามารถเลือกได้ เช่น a[4], a[7], a[9]
รูปแบบที่ไม่สามารถเลือกได้ เช่น a[1], a[2] เนื่องจากช่วงเวลาเดียวกัน (ที่ t = 2) มีกิจกรรมที่ทำพร้อมกัน 2 อัน

จากเคสนี้ solution ที่ดีที่สุดคือ a[1], a[3], a[6], a[8]
โดยวิธีแก้ปัญหานี้ด้วยอัลกอริทึมแบบ Greedy มีขั้นตอนดังนี้:

เรียงลำดับกิจกรรมตามเวลาสิ้นสุด เพราะเราต้องการเลือกกิจกรรมที่เสร็จสิ้นก่อน ซึ่งจะทำให้มีเวลามากที่สุดในการทำกิจกรรมถัดไป
เลือกกิจกรรมแรกจากลิสต์ที่เรียงแล้ว (โดยเรียงตามเวลาสิ้นสุด)
เลือกกิจกรรมถัดไปจากลิสต์ที่เรียงแล้ว ก็ต่อเมื่อเวลาเริ่มต้นของกิจกรรมนั้นมากกว่าหรือเท่ากับเวลาสิ้นสุดของกิจกรรมก่อนหน้าที่เลือกไว้
ทำซ้ำขั้นตอนที่ 3 จนกว่าจะครบทุกกิจกรรมในลิสต์

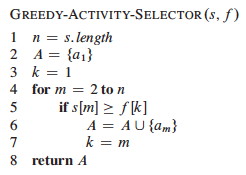
เมื่อเขียนเป็น code c++ ก็จะเป็นประมาณนี้

#include <algorithm>
#include <iostream>
#include <vector>

using namespace std;

// สร้างคลาสสำหรับเก็บข้อมูลกิจกรรม
class Activity {
public:
  int start, finish;
  Activity(int s, int f) {
    start = s;
    finish = f;
  }
};

// ฟังก์ชันสำหรับเปรียบเทียบกิจกรรมตามเวลาสิ้นสุด
bool compareActivities(Activity a1, Activity a2) {
  return a1.finish < a2.finish;
}

// ฟังก์ชันสำหรับแก้ปัญหาการเลือกกิจกรรม
void selectActivities(vector<Activity> &activities) {
  // เรียงลำดับกิจกรรมตามเวลาสิ้นสุด
  sort(activities.begin(), activities.end(), compareActivities);

  // เลือกกิจกรรมแรก
  int lastSelectedIndex = 0;
  cout << "Selected activities: " << activities[0].start << "-"
       << activities[0].finish;

  // เลือกกิจกรรมถัดไปที่ไม่ทับซ้อนกับกิจกรรมก่อนหน้า
  for (int i = 1; i < activities.size(); i++) {
    if (activities[i].start >= activities[lastSelectedIndex].finish) {
      cout << ", " << activities[i].start << "-" << activities[i].finish;
      lastSelectedIndex = i;
    }
  }
}

int main() {
  // สร้างชุดกิจกรรมตัวอย่าง
  vector<Activity> activities;
  activities.push_back(Activity(1, 3));
  activities.push_back(Activity(2, 5));
  activities.push_back(Activity(4, 7));
  activities.push_back(Activity(1, 8));
  activities.push_back(Activity(5, 9));
  activities.push_back(Activity(8, 10));
  activities.push_back(Activity(9, 11));
  activities.push_back(Activity(11, 14));
  activities.push_back(Activity(13, 16));

  // เรียกใช้ฟังก์ชันสำหรับแก้ปัญหาการเลือกกิจกรรม
  selectActivities(activities);

  return 0;
}

ผลลัพธ์ (ก็จะเหมือนกันกับตัวอย่างด้านบน)

Selected activities: 1-3, 4-7, 8-10, 11-14

โดย Time complexity ของ algorithm นี้ คือ O(nlogn) เนื่องจากต้องเรียงลำดับกิจกรรมก่อน จากนั้น solution ก็สามารถหาคำตอบได้ภายใน O(n) [วน loop 1 ลองและหยิบคำตอบออกมา)

Reference

https://www2.hawaii.edu/~suthers/courses/ics311f20/Notes/Topic-13.html

ตัวอย่าง Greedy Problem เทียบกับ Bluteforce​

Fractional Knapsack​

Activity Selection Problem​

Reference​

ตัวอย่าง Greedy Problem เทียบกับ Bluteforce

Fractional Knapsack

Activity Selection Problem

Reference